数字量子电子学的相关信息

　　量子

　　位经典的计算机位是 0 和 1，两个位形成四种可能的状态：00、01、10、11。通常，使用 n 位，您可以构建 2n 个不同的状态。n 个量子位可以得到多少个状态？由 n 个量子比特系统生成的状态空间的维数为 2n：在这个空间中归一化的每个向量代表一个可能的计算状态，我们将其称为 n 个量子比特的量子寄存器。量子比特数的这种指数增长表明，量子计算机具有以比经典计算机指数高的速度处理信息的潜在能力。请注意，对于 n = 200，您会得到一个大于宇宙中原子数的数字。

　　形式上，n 个量子位的量子寄存器是 2n 维希尔伯特空间 C2n 的一个元素，其计算基础由 n 个量子位的 2n 个寄存器形成。让我们考虑 2 个量子位的情况。与单个量子位类似，我们可以构建由向量 |00>、|01>、|10>、|11> 形成的状态空间的计算基础。具有 2 个量子位的量子寄存器是以下形式的重叠：

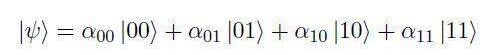
　　对系数的幅度进行归一化。

　　逻辑端口

　　与经典计算机一样，量子计算机由由基本量子逻辑门组成的量子电路组成。在经典情况下，只有一个（非平凡的）1 位逻辑端口，即 NOT 端口，它实现了通过真值表定义的逻辑否定操作，其中 1 → 0 和 0 → 1。

　　要在量子位上定义类似的操作，我们不能限制自己在主要状态 |0> 和 |1> 上建立其动作，但我们还必须指定处于状态 |0> 和 |0> 重叠状态的量子位如何操作。 1> 必须转化。直观上，NOT 应该交换两个主要状态的角色并将α |0> + β |1> 转换为β |0> + α |1>。

　　显然，|0> 会变成 |1>，而 |1> 会变成 |0>。实现这种类型转换的操作是线性的，是量子力学的一个普遍性质，经实验证明是正确的。

　　对应于量子 NOT 的矩阵因历史原因 X 被调用，定义为：

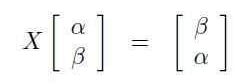
　　在归一化条件|α|2 + |β|2 = 1 任何量子态α |0> + β |1>。

　　除了 NOT，Z 矩阵表示两个重要的操作：

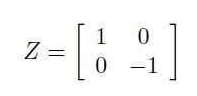
仅作用于组件 |1> 交换其符号和 Hadamard 端口：

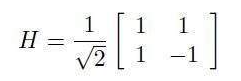
　　最后一个操作经常用于定义量子电路。它的作用是将基本状态转换为重叠，在计算基础中进行测量后，结果为 0 或 1 的概率相等。H 的影响可以定义为对半执行 NOT ，因此结果状态既不是 0 也不是 1，而是两个主要（基本）状态的相干叠加。

　　在两个经典位上实现操作的最重要的逻辑端口是 AND、OR、XOR、NAND 和 NOR 端口。NOT 和 AND 端口形成一个通用集；即，任何布尔函数都可以通过这两种操作的组合来实现。出于同样的原因，NAND 形成了一个通用集。

　　XOR 的量子等价物是受控非 (CNOT) 端口，它在 2 个量子位上运行：第一个是控制量子位，第二个是目标量子位。如果控制为0，则目标保持不变；如果控制为 1，则目标被否定。那是：

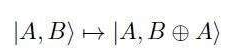
　　其中 A 是控制量子位，B 是目标，⊕ 是经典的 XOR 运算（图 1）。

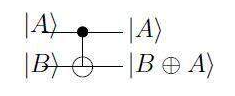
图 1：CNOT 端口

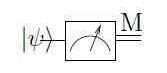
图 2：量子测量电路

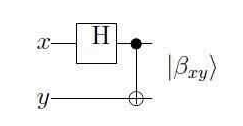
图 3：用于创建贝尔态的量子电路

　　另一个重要的操作由图 2 中的符号表示，包括测量一个量子位 |ψ> = α |0>+β |1>。结果是一个经典的位 M（用双线表示），它将是 0 或 1。

　　CNOT 端口可用于创建纠缠状态。图 3 中的电路为计算基础 |00>、|01>、|10>、|11> 的每个状态生成一个特定的纠缠状态。这些状态，我们用 β00、β10、β01、β11 表示，称为贝尔或 EPR 状态（贝尔、爱因斯坦、波多尔斯基和罗森，他们首先发现了它们的非凡特性）。

　　量子 CMOS

　　在现代数字计算机中编码信息的方法是通过集成电路中微型晶体管上的电压或电流，这些晶体管充当数字或模拟元件。每个晶体管由能够定义 0（低电压）或 1（高电压）状态的总线寻址。

　　量子计算机有不同的相似之处，其基本思想如图 4 所示。在这个图中，我们观察到一个超导量子位（也称为 SQUID — 超导量子干涉装置），它是量子计算机（量子“晶体管”）的基本元件。术语“干涉”是指电子，其行为类似于量子波中的波，干涉模式会引起量子效应。

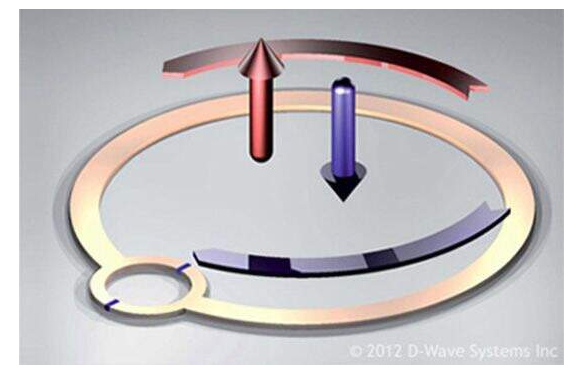
　　图 4：超导量子位的布局

       箭头表示编码信息位值的磁自旋状态。与普通信息位不同，这些状态可以置于量子力学叠加中。（图片：D-Wave）

　　在这种情况下，基本元素是铌，而不是传统晶体管中的硅。材料的特性允许电子表现得像量子位。当金属冷却时，它被称为超导体并开始显示量子力学效应。超导量子位结构将两种状态编码为指向相反方向的微小磁场。通过量子力学，我们可以控制这些定义为 +1 和 –1 或 |ψ> = α |0>+β |1> 的状态。

　　通过称为超导回路耦合器的元件，创建了多量子位处理器。可以通过将许多这些元素（例如量子位和耦合器）放在一起来设计可编程量子设备（图 5）。

　　为了控制量子位的操作，重要的是要有一个由约瑟夫森结组成的开关结构，它引导每个量子位（将磁信息脉冲路由到芯片上的正确点）并将信息存储在本地磁存储元件中每个设备。

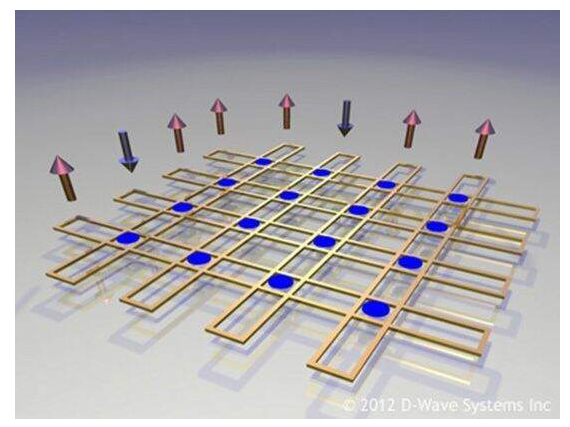
　　图 5：8 个量子位的示意图

       蓝点是允许量子位交换信息的 16 个耦合元件的位置。（图片：D-Wave）

　　约瑟夫森效应是由绝缘结隔开的两个超导体之间的电流发展，称为约瑟夫森结。这种效应是由于每个超导体中电子对的隧道效应造成的。如果绝缘子太宽，隧道效应的概率就低，不会出现这种效应。

　　大多数约瑟夫森结代表一个量子处理单元（QPU）。QPU 没有大面积的内存（缓存），因为它们的设计更像是一个生物大脑，而不是传统硅处理器的常见冯诺依曼架构。人们可以将量子位视为神经元，将耦合器视为控制这些神经元之间信息流的突触。

　　成功实现量子的要求被封装在量子比特的数量中，量子比特的数量必须足够大才能实现高效率。这也意味着您必须能够在短时间内执行大量量子位操作。这些算法需要在许多量子位上应用许多逻辑门。为了保持足够低的错误概率，门必须非常精确。

文章来源：eeweb Maurizio Di Paolo Emilio

编辑：ymf