

宽带数字接收机的信道化设计
处理器/DSP
描述
宽带数字接收机的信道化设计
0 引言
在现代电子战环境中,信号一般都具有密集化、复杂化的特点,而且占用的频谱越来越宽,从而对宽带数字信道化接收机准确接收信号提出了更高的要求。一般的多相滤波器在监视整个频段时,由于相邻信道间往往会存在盲区,有可能丢失信号。而改进后的无盲区多相滤波器的信道数与抽取倍数不再相等。一般的旋转开关方法实现延迟和抽取只适用于信道数与抽取倍数相等的情况,而无法适应改进后的算法。但是,信道数和抽取因子之间往往存在倍数关系。本文正是利用这一关系解决了延迟与抽取的问题,并完成了整个复多相滤波器的FPGA设计。
1 复信号多相滤波器无盲区算法分析
复信号多相滤波器的作用是用D个信道将-fs/2~fs/2频段均匀划分,然后用输入信号S(n)以复本振信号,再将特定频段的信号搬移到基带,并通过低通滤波器得到位于该信道的信号,然后进行抽取,以降低数据速率。无盲区的信道划分如图1所示。由于其相邻信道有50%的重叠,因此,相邻信道间不存在盲区,故能对信号进行全概率捕获。
为了防止频谱混叠,其抽取倍数应为D/2。这样,多相滤波器的第k路输出推导如下(D’=D/2时):

由式(2)可知,该算法是对多相滤波器的输入数据进行D/2倍的抽取,各多相分量是由原低通滤波器的系数先进行D抽取再做两倍内插得到的。根据式(2)可以得到如图2所示的数学模型和FPGA设计。
2 FPGA设计
2.1延迟和抽取
以下选用具体的例子来阐述复多相滤波器的FPGA设计方法。对于8信道的多相滤波器,其抽取因子为4的情况,经过延迟单元进入各抽取器的顺序如表1所列。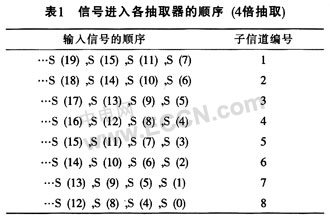
观察表1可知,进入每个子信道的数据都是4倍抽取。而且4信道比8信道延迟一个数据,3信道比7信道延迟一个数据,依此类推。这样,就可以将信道分为两部分,即1、2、3、4信道是一部分,5、6、7、8信道是另一部分。
由于每个子信道的滤波系数为12个,即每个抽取器必须同时输出12个数据与一个子信道的12个滤波系数进行乘加运算。采用可定制模块shift_tap,能够满足这样的延迟和抽取要求,它的输出即为抽取器的输出。若将shift_tap中的抽取因子设为4,一次同时输出13个数据,那么,第一次输出的13个数据为x(0)、x(4)、x(8)、……、x(56),这样可将1-12送入8信道,2-13送入4信道进行乘加运算;而第二次输出的13个数据为x(1)、x(5)、x(9)……、x(57),其中1-12送入7信道,2-13送人3信道,依此类推……这样,每个时钟节拍将得到两个信道的延迟和抽取输出,因而需要4次这样的操作才能完成一次所有信道的延迟和抽取。然后再重复执行以上操作。
2.2 滤波器的多相分量
设计多相分量时,首先可根据原低通滤波器的频率响应确定所需的滤波器类型和阶数,以求出冲击响应h(n);然后再根据式hp(m)=h(mD+p),D=8,p=0,1,…D-1来确定多相分量。
若采样频率fs为64 MHz,并把64 MHz带宽均匀划分为8路子信道,则每路通带的带宽为8MHz。图3所示是原型低通滤波器的频率响应图。
MATLAB中的firpmord函数,一般采用的是最佳逼近最大最小准则算法,该算法可以求出原型低通滤波器的阶数,而firpm函数可以求出原型低通滤波器的系数。即:
a=firpmord([4 8],[1 0],[0.001 0.001],64);(3)
h=firpm(a,[0 4/32 8/32 1],[1 1 0 0]); (4)
(3)式中, [4 8]表示通带截止频率为4MHz,阻带截止频率为8 MHz; [1 0]表示通带幅度为1,阻带幅度为0; [0.001 0.001]表示通带、阻带波动均为0.001;64表示采样频率为64MHz。
而在(4)式中,[04/32 8/32 1]分别为对应于实际频率0、4、8、32(MH)的归一化频率;[1 1 0 0]为上述频率点上的幅度值。
求出原低通滤波器h(n)后,就可以求出多相滤波器的多相分量。图2中的多相分量是对h(n)进行8倍抽取,再做两倍内插得到的。用MATLAB语句可方便地得到各多相分量的系数,每个多相分量有6个非零系数,两倍内插后为12个系数。其MATLAB语句如下:
hp=zeros(8,2*fix(length(h)/8));
for i=1:8
hp (i,1:2:end)=h(i:8:(fix(lengh (h)/8)-1)*8+i);
end
一个多相分量的滤波运算可用三个乘加单元完成,每个乘加单元有四个乘法器,这样就可以完成12个系数的乘加。多相分量的滤波系数一般事先都将其转换为二进制补码存放在ROM中。
由上述分析可知,每个时钟节拍可完成两个信道的延迟和抽取(采用流水线操作),每个时钟节拍需要进行两个多相分量的乘加运算,即需要同时得到12个非零系数,这可用12个单口ROM实现。其中6个ROM存放1~4信道的系数。另6个ROM存放5~8通道的系数。其存储格式如表2和表3所列。
这样,每当时钟上升沿到来时,就可以同时输出两个子信道的12个非零系数。通常可以设计一个模4减法计数器来实现ROM地址的产生。当数据准备好后,发出一个计数器的使能信号,计数器开始计数。因为首先计算的是4信道和8信道,所以,计数器的初始值为3,采用减一计数,计数到0后再进行循环。
2.3 时序的设计
由于信号s(n)的输入速率为64 MHz。故在64 MHz时钟驱动下,每一个节拍计算两个子信道,8个信道的计算需要用4个节拍来完成,并得到8个复数。这8个复数必须同时进入FFT模块,所以,可在FFT之前设计一组乒乓RAM来接收这8个复数。其中一个RAM以64 MHz的速率存放前面的计算结果,每个节拍接收两个复数,4个节拍接收完8个复数后开始FFT运算,同时换成另一个RAM接收前面的计算结果。等到8个复数都存放好之后,再开始FFT运算,此时又再次换成第一个RAM接收前面的计算结果,并依次循环。根据这样的时序设计,FFT模块的时钟应为16 MHz。FFT运算由IP核完成。经FFT运算后同时可得到8个复数形式的结果,由于复数分成实虚部的表示形式,且实虚部都用32位二进制数表示,因此,8个复数需要16个32位的二进制数表示,也就是芯片上需要16×32=512个引脚,这对于任何芯片都是不可能办到的。为此,应在FFT模块的输出端也设计一个乒乓RAM。其中一个RAM先将8个FFT运算结果存储起来,然后以64 MHz的时钟频率每个节拍向外输出两个复数(即4个32为二进制数),直到4个节拍全部输出完毕(即8个复数全部输出的频率为16 MHz),同时另一个RAM以16MHz的时钟频率接收FFT的运算结果。然后将两个RAM的作用交换,再以此循环。
3 结束语
本文详细分析了复信号多相滤波器的无盲区改进算法,并根据推导出的数学模型完成了其FPGA的设计。该设计根据信道数和抽取因子之间的倍数关系,解决了延迟和抽取功能的实现问题,并使用乒乓RAM实现了复信号多相滤波器的多通道流水线输出。
-
如何设计宽带数字接收机的信道化?2019-08-06 0
-
求一种数字信道化IFM接收机的高效实现方案2021-02-23 0
-
请问怎样去设计一种宽带信道化接收机?2021-05-31 0
-
基于多相滤波的宽带数字化接收机技术2009-02-21 627
-
基于软件无线电的数字化接收机的研究2010-07-17 475
-
基于FPGA的信道化接收机2010-07-21 478
-
宽带数字接收机的设计实现2010-12-28 478
-
基于多相滤波的数字信道化阵列接收机2010-09-13 1986
-
宽带数字信道化接收机的FPGA实现2011-03-07 891
-
短波宽带接收机信道化的仿真实现2011-09-30 946
-
基于FPGA的信道化接收机2017-12-07 1040
-
基于一种宽带数字接收机的信道化设计2017-12-09 5023
-
如何使用FPGA实现高效的宽带数字接收机2021-02-05 1016
-
基于多级信道化的超宽带搜索接收机设计与实现2021-03-19 759
全部0条评论

快来发表一下你的评论吧 !

