奇偶校验码,奇偶校验码原理是什么?

奇偶校验码,奇偶校验码原理是什么?

奇偶校验码是奇校验码和偶校验码的统称，是一种最基本的检错码。它是由n-1位信息元和1位校验元组成，可以表示成为（n，n-1）。如果是奇校验码，在附加上一个校验元以后，码长为n的码字中“1”的个数为奇数个；如果是偶校验码，在附加上一个校验元以后，码长为n的码字中“1”的个数为偶数个。设：如果一个偶校验码的码字用A=[an-1,an-2,…，a1,a0]表示，则：

式中 为校验元，“+”为模二和（以后也这样表示，请注意）。式（1）通常被称为校验方程。利用式（1），由信息元即可求出校验元。另外，如果发生单个（或奇数个）错误，就会破坏这个关系式，因此通过该式能检测码字中是否发生了单个或奇数个错误。

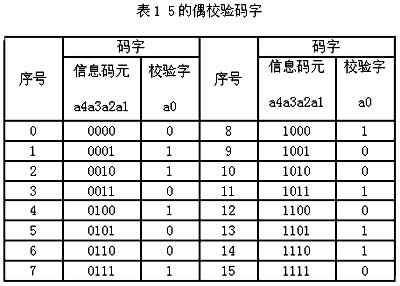
奇偶校验码是一种有效地检测单个错误的方法，之所以将注意力集中在检（或纠）单个错，这主要是因为码字中发生单个错误的概率要比发生2个或多个错误的概率大得多。例如，n = 5的码字，如果码字中各码元的错误是互相独立，误码率为10-4，则错1、2、3、4和5位的概率分别为：5×10-4、10-7、10-11、10-16和10-20。由此可见，要检（或纠）错误，首先要解决单个错误，这样才抓住了主要矛盾。一般情况下用上述偶校验码来检出单个错误，检错效果是令人满意的，不仅如此，奇偶校验码的编码效率很高，R=(n-1)/n，随n增大而趋近于1。下面就给出以码长n＝5为例，利用表1列出全部偶校验码字.

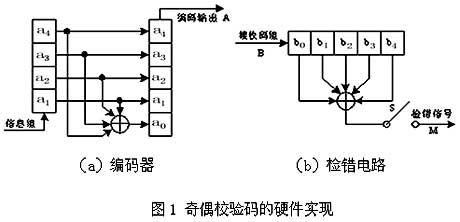
在数字信息传输中，奇偶校验码的编码可以用软件实现，也可用硬件电路实现。图8-4(a)就是码长为5的偶校验码编码器。从图中可以看到，4位码元长的信息组，串行送入四级移位寄存器（输入定时缓冲器），同时经模二运算得到校验元，存入输出缓冲器末级，编码完成即可输出码字。接收端的检错电路如图1(b)所示。当一个接收码组B完全进入五级移存器内时，开关S立即接通，从而得到检错信号M=b4+b3+b2+b1+b0。如果接收码组B无错，B＝A，则M＝0；如果接收码组B有单个（或奇数个）错误，则M＝1。

[编辑]

行列校验码

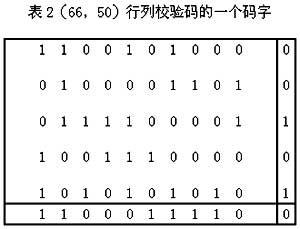
行列校验码又称作水平垂直一致校验码或二维奇偶校验码，有时还被称为矩阵码。它不仅对水平（行）方向的码元，而且还对垂直（列）方向的码元实施奇偶校验。一般L×m个信息元，附加L+m+1个校验元，由L+1行，m+1列组成一个（Lm+L+m+1，Lm）行列校验码的码字。表8-2就是（66，50）行列校验码的一个码字（L＝5，M＝10），它的各行和各列对l的数目都实行偶数校验。可以逐行传输，也可以逐列传输。译码时分别检查各行、各列的校验关系，判断是否有错。

这种码有可能检测偶数个错误。因为每行的校验位虽然不能用于检测本行中的偶数个错码，但按列的方向就有可能检测出来。可是也有一些偶数错码不可能检测出，例如，构成矩形的四个错码就检测不出来。

这种二维奇偶校验码适于检测突发错码。因为这种突发错码常常成串出现，随后有较长一段无错区间，所以在某一行中出现多个奇数或偶数错码的机会较多，这种方阵码适于检测这类错码。前述的一维奇偶校验码一般只适于检测随机错误。

由于方阵码只对构成矩形四角的错码无法检测，故其检错能力较强。一些试验测量表明，这种码可使误码率降至原误码率的百分之一到万分之一。

二维奇偶校验码不仅可用来检错，还可用来纠正一些错码。例如，当码组中仅在一行中有奇数个错误时，则能够确定错码位置，从而纠正它。

[编辑]

恒比码

恒比码又称作等重码,这种码的码子中1和0的位数保持恒定比例。由于每个码字的长度是相同的，若1、0恒比，则码字必等重。

若码长为n，码重为w，则此码的码字个数为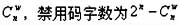。该码的检错能力较强，除对换差错（1和0成对的产生错误）不能发现外，其它各种错误均能发现。

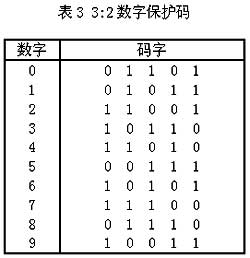
目前我国电传通信中普遍采用3：2码，该码共有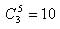个许用码字，用来传送10个阿拉伯数字，如表8-3所示。这种码又称为5中取3数字保护码。因为每个汉字是以四位十进制数来代表的，所以提高十进制数字传输的可靠性，就等于提高汉字传输的可靠性。实践证明，采用这种码后，我国汉字电报的差错串大为降低。

目前国际上通用的ARQ电报通信系统中，采用3：4码即7中取3码，这种码共有个许用码字，93个禁用码字。35个许用码字用来代表不同的字母和符号。实践证明，应用这种码，使国际电报通信的误码率保持在以10-6下。