量子密码技术,量子密码技术原理解析

量子密码技术,量子密码技术原理解析

在今天的信息时代,大量的敏感信息如病历、法庭记录、资金转移、私人财产等常常通过公共通信设施或计算机网络来进行交换,而这些信息的秘密性和真实性是人们迫切需要的.密码学经过传统的秘密密钥加密体制、公共密钥加密体制长期的演绎和发展,各种理论和算法推陈出新,极大推动了网络信息一体化的蓬勃发展.然而,当理性地看待今天网络安全技术的现状和展望其未来的发展趋势时,不得不更多地从总体和长远性来思考一直困扰着密码设计者的系统体制问题.

图1所示典型加密系统是通过密钥K将明文P转换成密文C,放在公共信道上发送,在接受方进行逆变换的解密恢复可读明文.其安全性在于通信双方首先能在安全信道上传递密钥,一次一密钥方案(注意:密钥K长度应不小于明文P的长度,即熵H(K)≥H(P)).C.E.Shannon证明是绝对安全的.可是在几乎所有应用系统里,这几乎是不可能实现的,尤其致命的是:既然通信双方要进行保密通信,他们首先必须获得密钥,即需要进行获得密钥的秘密通信,但这种安全性是得不到证明的,通信双方对是否存在窃听者毫无所知；这就是在保密通信中经常涉及到的“Catch 22”问题,原因在于密钥的建立过程总要利用某种载体的某种物理属性,而经典物理学指出,测量该载体的这些属性对其不会产生任何影响.

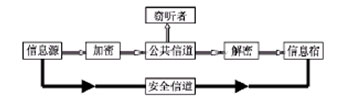
图1　典型通信加密系统

解决“Catch 22”问题一种方案是现代密码学中的公钥密码体制(PKCS),如图2所示.通信双方可以建立各自的加密／解密密钥对(Ek,Dk),将加密密钥Ek公开同时,各自妥善保管专有解密密钥Dk,这种加密体制的安全性大多建立在一些著名的数学难题基础之上,通过设计单向陷门函数以实现加解密算法的不可逆性(至少在现有的资源和算法下是不现实的).从理论上说,由公开密钥获得秘密密钥在计算上是不可能的,“Catch 22”问题似乎得到了解决,但到目前为止还没有人能证明是否存在真正的单向陷门函数,因此也就没有人真正了解公钥密码体制的安全强度.从根本上说,公钥体制是在一定程度上绕过了“Catch 22”问题,随着数学和计算技术的快速发展,特别是最近发展的量子计算技术,当量子计算机成为现实时,公钥密码体制将可以很容易地被破译,例如应用肖氏(Shor's)量子分解因式算法可以在多项式时间内轻易地破解RSA加密算法.另一个缺陷是众多实际应用中的公钥密码系统,其密钥往往由密钥管理中心独立管理,因此在收发方进行保密通信之前仍然需要通过秘密信道与管理中心通信.基于此,公钥体制没有彻底解决“Catch 22”问题.而量子密码体制提供了可证明的安全性和对外界干扰的检测性［1］,从而解决了“Catch 22”这个一直未能解决的重要问题.

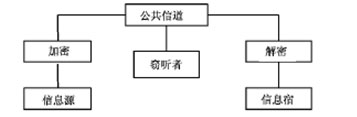
图2　公开密钥加密体系

现代密码学认为,任何加密体系的加、解密算法都是可以公开的,其安全性应该在于密钥的保密性.量子密码方案在密钥分配协议中提供了传统密码体制所无法比拟的潜在优势:具有可证明的安全性；能在密钥生成之前进行量子通信以检测侵入者的威胁,为此它为未来的保密通信提供了最终确实的保障.以下在涉及正题之前先作一个大致的描述:

首先通信发送者随机选择一二进制序列,序列中的每一比特都由随机选择的具有某量子态(例如偏振态)的单光子代表,从而在真正物理意义上是发送一串特定时间间隔的单光子序列,接收方则保持同步地随机选择探测方法,独立地探测光脉冲中各单光子状态,如果探测到了一个光子,他就记录下探测到它的时间、结果、方法；发送接收完毕后,双方在公共信道里讨论光子序列的总体接收情况,接收方告诉发送方他接收到各光子的时间和探测方法,但不通报结果；发送方根据自己的发送记录与反馈信息,通知接收方哪些光子的接收方法是正确的,摒弃那些未被接收到的光子和探测方法错误的光子,接收方根据提示从所收到的初始光子序列中提取有用的比特,建立起初始密钥(Raw key)；而后通信双方再任意从初始密钥中选取一部分,逐个比较比特值,判断误码率是否超出了误差阈值(藉此推断窃听者是否存在),在未超出情况下去除初始密钥测试部分,余下的比特序列再经过一定的误差校验算法构成正式通信密钥,否则放弃所有数据,检查通道,重头开始通信.

量子密码理论

量子物理与经典物理最重要的区别可以概括为互补性和相关性.常说的波粒二象形就是一个量子体系的两种互补属性,在著名的杨氏双缝实验中,如果想确知发出的某光子通过哪个缝隙,因而来探测系统的微粒性,结果将导致无法观测到光的干涉现象；同样,如果想观测光的干涉现象,所以测量系统的波动性时,就无法确定光子通过的路径.量子密码技术正是应用了这一互补性以及量子力学的基本理论［2,3］,包括海森伯格测不准原理和单光子的不可分割性,从而解决了经典密码学一直无法妥善处理的安全性问题,表述如下:

设A和B分别是表示一个量子体系两力学量的算符,二者不对易,即 [A,B］=AB-BA≠0,　　(1) 这意味着,A和B不能同时有确定值,在同一个态ψ中,A和B不确定程度满足下列关系: <(ΔA)2〉〈(ΔB)2≥1/4‖〈［A,B］〉‖2,　　(2) 注:ΔA=A-〈A〉; ΔB=B-〈B〉;

<(ΔA)2〉代表算符A的均方偏差;〈(ΔB)2〉代表算符B的均方偏差. 海森伯格测不准原理说明,微观粒子两类非相容可观测态的属性是互补的,对其中一种属性的精确测量必然会导致其互补属性的不确定性.在量子力学中,一个物质体系(例如一个电子或一个光子)是用希耳伯特空间中的一个态矢量来表示,体系的每种物理属性(例如坐标或动量)均用专有算符表示,而每个算符的所有本征态(组成完全系)构成希耳伯特空间中一组相互正交的基态(基矢),任何态矢量都可以按照一个完全系的基矢进行展开,例如:态矢量|ψ〉,按照算符A的本征态展开如下:

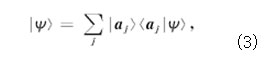
注:aj是算符A在各本征态的本征值,满足方程A|aj〉=aj|aj〉,式(3)说明,对算符A进行数值测量,测量结果为aj,同时使被测量体系处于新的态矢量|aj〉的概率为‖〈aj|ψ〉‖2.具体说,就是在量子通信中,窃听者对传送的光子序列所进行的任何干扰、窃听,例如量子拷贝、截取/重发等,都将导致光子状态的改变,从而影响接收者的测量结果,由此可对窃听者的行为进行判定和检测.现在假设如图3.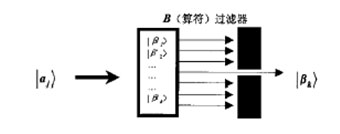

图3　正常量子信道发-收模型

态矢量|aj〉入射到B(算符)过滤器上,只允许其本征态|βk〉(满足B|βk〉=βk|βk〉) 通过,根据展开式: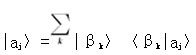测量的本征值为βk的概率为‖〈βk|aj〉‖2.如果态矢量|aj〉按照另一个算符E的本征态进行展开: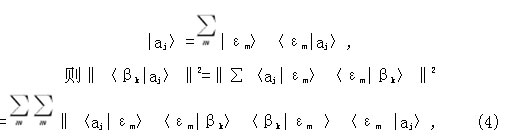假若态矢量|aj〉在入射到B(算符)过滤器之前,被插入E(算符)过滤器,见图4.那么此系统最终测得本征值为βk的所有可能的概率总计为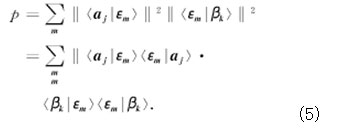

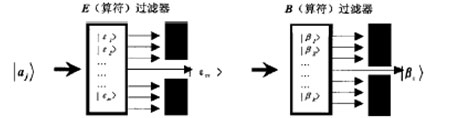
图4　存在窃听者的量子信道模型

通过比较式(4)和(5),可以得出:

用双缝试验进行类比来形象说明的话,E(算符)过滤器就相当于检测光子的精确轨迹,式(5)是代表波动性的干涉现象遭到破坏后的结果数学表达式.那么能鉴别出中途是否进行过测量吗？可以.因为无法鉴别就是要式(5)和(6)相等,这必须满足:

因此只要算符A和B本身是相容的可观测态,而E与A、B不对易(属性互补),通过对B(算符)过滤装置输出结果进行数理统计,就能检测出是否应用过E(算符)过滤器进行了干扰.以下重点介绍量子密钥分发协议,深入了解一下实际运作的量子密码术。