基于有效样本的类别不平衡损失

导读

使用每个类的有效样本数量来重新为每个类的Loss分配权重，效果优于RetinaNet中的Focal Loss。

本文综述了康奈尔大学、康奈尔科技、谷歌Brain和Alphabet公司的基于有效样本数的类平衡损失（CB损失）。在本文中，设计了一种重新加权的方案，利用每个类的有效样本数来重新平衡损失，称为类别平衡损失。

1. 类别平衡问题

假设有像上面那样的不平衡的类。head：对于索引小的类，这些类有较多的样本。Tail：对于大索引的类，这些类的样本数量较少。黑色实线：直接在这些样本上训练的模型偏向于优势类。红色虚线：通过反向类频率来重新加权损失可能会在具有高类不平衡的真实数据上产生较差的性能。蓝虚线：设计了一个类平衡项，通过反向有效样本数来重新加权损失。

2. 有效样本数量

2.1. 定义

数据间信息重叠，左：特征空间S，中：1个样本数据的单位体积，右：数据间信息重叠

直觉上，数据越多越好。但是，由于数据之间存在信息重叠，随着样本数量的增加，模型从数据中提取的边际效益会减少

左：给定一个类，将该类的特征空间中所有可能数据的集合表示为S。假设S的体积为N且N≥1。中：S子集中的每个样本的单位体积为1，可能与其他样本重叠。Right：从S中随机抽取每个子集，覆盖整个S集合。采样的数据越多，S的覆盖率就越好。期望的采样数据总量随着样本数量的增加而增加，以N为界。

因此，将有效样本数定义为样本的期望体积。

这个想法是通过使用一个类的更多数据点来捕捉边际效益的递减。由于现实世界数据之间的内在相似性，随着样本数量的增加，新添加的样本极有可能是现有样本的近重复。另外，cnn是用大量的数据增广来训练的，所有的增广实例也被认为与原始实例相同。对于一个类，N可以看作是唯一原型的数量。

2.2. 数学公式

En表示样本的有效数量（期望体积）。为了简化问题，不考虑部分重叠的情况。也就是说，一个新采样的数据点只能以两种方式与之前的采样数据交互：完全在之前的采样数据集中，概率为p，或完全在原来的数据集之外，的概率为1- p。

有效数字：En = （1−β^n）/（1−β），其中，β = （N− 1）/N，这个命题可以用数学归纳法证明。当E1 = 1时，不存在重叠，E1 =（1−β^1）/（1−β） = 1成立。假设已经有n−1个样本，并且即将对第n个样本进行采样，现在先前采样数据的期望体积为En −1，而新采样的数据点与先前采样点重叠的概率为 p = E（n−1）/N。因此，第n个实例采样后的期望体积为：

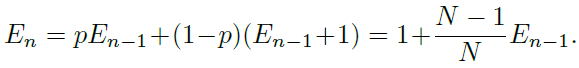
此时：

我们有：

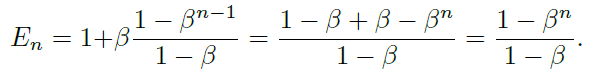
上述命题表明有效样本数是n的指数函数。超参数β∈［0，1）控制En随着n的增长有多快。

3. 类别平衡 Loss （CB Loss）

类别平衡（CB）loss可以写成：

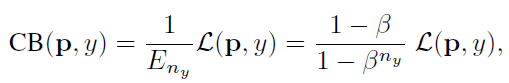
其中，ny是类别y的ground-truth的数量。β = 0对应没有重新加权， β → 1对应于用反向频率进行加权。

提出的有效样本数的新概念使我们能够使用一个超参数β来平滑地调整无重权和反向类频率重权之间的类平衡项。

所提出的类平衡项是模型不可知的和损失不可知的，因为它独立于损失函数L和预测类概率p的选择。

3.1. 类别平衡的 Softmax 交叉熵损失

给定一个标号为y的样本，该样本的softmax交叉熵（CE）损失记为：

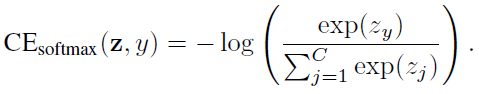
假设类y有ny个训练样本，类平衡（CB）softmax交叉熵损失为：

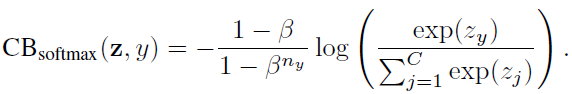
3.2. 类别平衡的 Sigmoid 交叉熵损失

当对多类问题使用sigmoid函数时，网络的每个输出都执行一个one-vs-all分类，以预测目标类在其他类中的概率。在这种情况下，Sigmoid不假定类之间的互斥性。由于每个类都被认为是独立的，并且有自己的预测器，所以sigmoid将单标签分类和多标签预测统一起来。这是一个很好的属性，因为现实世界的数据通常有多个语义标签。sigmoid交叉熵（CE）损失可以写成：

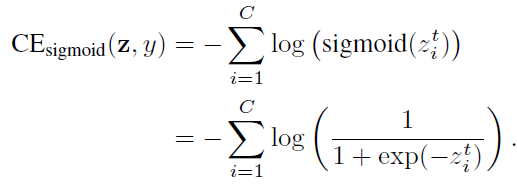
类平衡（CB） sigmoid交叉熵损失为：

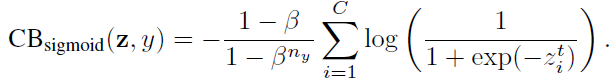
3.3. 类别平衡 Focal Loss

Focal loss （FL）是在RetinaNet中提出的，可以减少分类很好的样本的损失，聚焦于困难的样本。

类别平衡的 （CB） Focal Loss为：

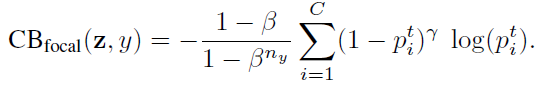
4. 实验结果

4.1. 数据集

试验了CIFAR-10和CIFAR-100的5个不平衡系数分别为10、20、50、100和200的长尾版本。iNaturalist 和ILSVRC是天然的类别不平衡数据集。

上面显示了每个类具有不同不平衡因素的图像数量。

4.2. CIFAR 数据集

loss类型的超参数搜索空间为{softmax， sigmoid， focal}， ［focal loss］的超参数搜索空间为β∈{0.9，0.99，0.999，0.9999}，γ∈{0.5，1.0，2.0}。在CIFAR-10上，最佳的β一致为0.9999。但在CIFAR-100上，不同不平衡因子的数据集往往有不同且较小的最优β。

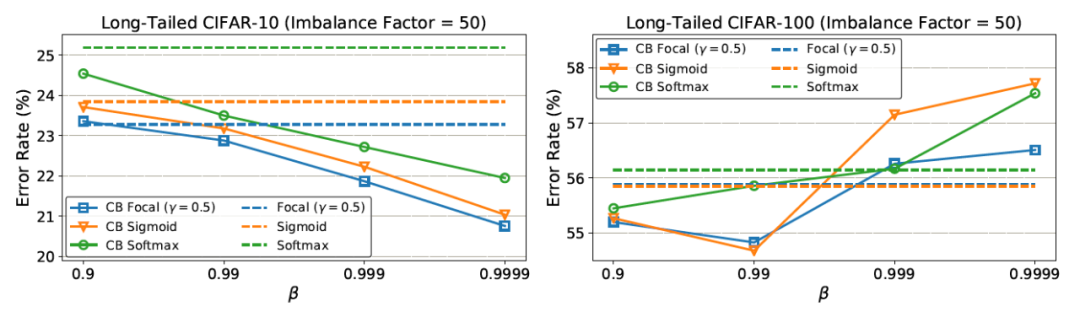
有和没有类平衡项时的分类错误率

在CIFAR-10上，根据β = 0.9999重新加权后，有效样本数与样本数接近。这意味着CIFAR-10的最佳重权策略与逆类频率重权类似。在CIFAR-100上，使用较大的β的性能较差，这表明用逆类频率重新加权不是一个明智的选择，需要一个更小的β，具有更平滑的跨类权重。例如，一个特定鸟类物种的独特原型数量应该小于一个一般鸟类类的独特原型数量。由于CIFAR-100中的类比CIFAR-10更细粒度，因此CIFAR-100的N比CIFAR-10小。

4.3. 大规模数据集

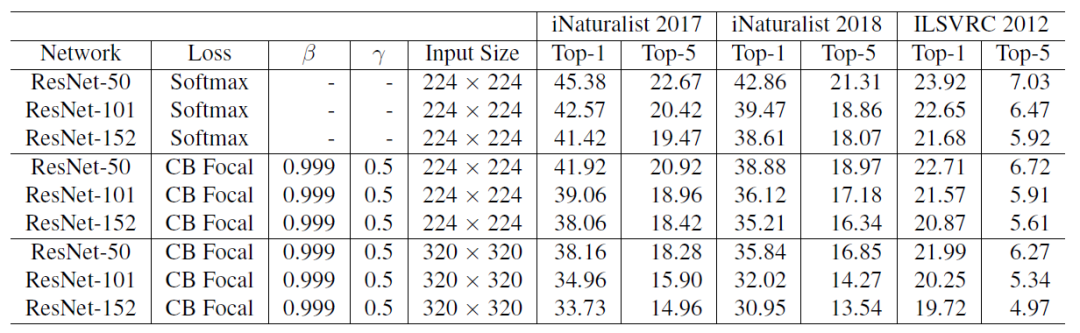
在所有数据集验证集上，使用不同损失函数训练的大规模数据集上的Top-1和Top-5分类错误率

使用了类平衡的Focal Loss，因为它具有更大的灵活性，并且发现β = 0.999和γ = 0.5在所有数据集上都获得了合理的良好的性能。值得注意的是，使用了类别平衡的Focal Loss来代替Softmax交叉熵，ResNet-50能够达到和ResNet-152相应的性能。

以上数字显示类平衡的Focal Loss损失经过60个epochs的训练后，开始显示其优势。

英文原文：https://medium.com/nerd-for-tech/review-cb-loss-class-balanced-loss-based-on-effective-number-of-samples-image-classification-3056a1a1a001

作者：Sik-Ho Tsang

编译：ronghuaiyang（AI公园）

编辑：jq