Matlab低通滤波器设定与实践

Matlab数字滤波器设计实践—FIR

1低通滤波器设定

在理想情况下，低通滤波器使信号中低于指定截止频率 ωc 的所有频率分量保持不变，并拒绝高于 ωc 的所有分量。由于实现理想低通滤波器所需的脉冲响应是无限长的，因此无法设计出理想的 FIR 低通滤波器。理想脉冲响应的有限长度逼近会导致滤波器的通带 （ω《ωc） 和阻带 （ω》ωc） 中都出现波纹，并导致通带和阻带之间的过渡带宽度非零。

当用有限脉冲响应逼近时，通带/阻带波纹和过渡带宽度都是不希望出现的，且不可避免地与理想低通滤波器存在偏差。下图说明了这些偏差：

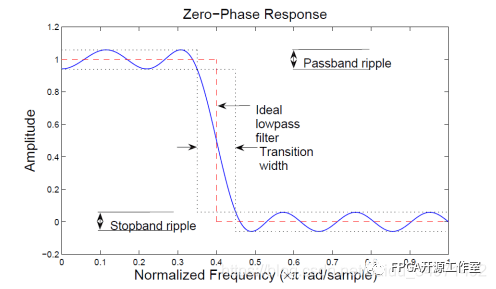
实际的 FIR 设计通常包括过渡带宽度和最大通带和阻带波纹不超过允许值的滤波器。除了这些设计设定之外，还必须选择滤波器阶数，它等效于选择截断的脉冲响应的长度。

滤波器设计中的设计设定可形象地比喻为下图所示的三角形，每个设定对应其中一个角。

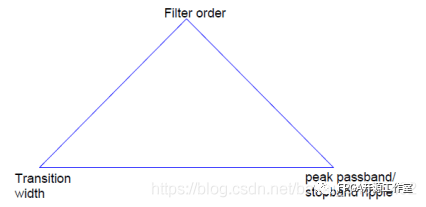
三角形相当于选择设计设定时可用的自由度。由于各角之和是固定值，因此最多只能选择两个设定的值。第三个设定将由特定设计算法确定。此外，就像三角形中的各角一样，如果我们使一个设定更大/更小，它将影响其他一个或两个设定。

FIR 滤波器广受欢迎，因为它们非常稳定，并可以设计成具有线性相位的滤波器。尽管如此，这些滤波器仍可能有长瞬时响应，在某些应用中的计算成本可能很高。

2 最小阶 FIR 设计

通过指定通带和阻带频率以及通带波纹和阻带衰减，可以获得最小阶设计。然后，设计算法会选择符合设定的最小滤波器长度。

设计最小阶低通 FIR 滤波器，其通带频率为 0.37pi 弧度/采样点，阻带频率为 0.43pi 弧度/采样点（因此过渡带宽度等于 0.06*pi 弧度/采样点），通带波纹为 1 dB，阻带衰减为 30 dB。

Fpass = 0.37;

Fstop = 0.43;

Ap = 1;

Ast = 30;

d = designfilt（‘lowpassfir’，‘PassbandFrequency’，Fpass，。..

‘StopbandFrequency’，Fstop，‘PassbandRipple’，Ap，‘StopbandAttenuation’，Ast）;

hfvt = fvtool（d）;

可以使用 filtord 函数查询生成的滤波器阶数。

可以使用 filtord 函数查询生成的滤波器阶数。

N = filtord（d）

N = 39

可以使用 info 函数获取用于设计滤波器的参数的有关信息

info（d）

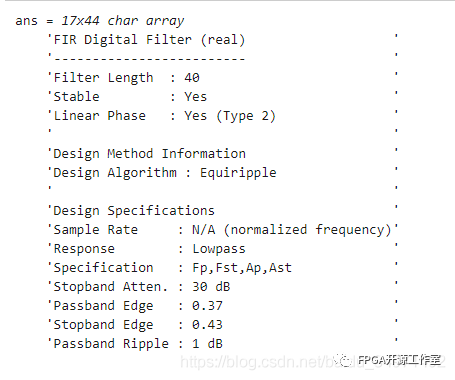
默认情况下，designfilt 函数会选择一个等波纹设计算法。线性相位等波纹滤波器是令人满意的，因为对于给定阶数，这种滤波器与理想滤波器的最大可能偏差最小。

然而，请注意，也可以使用 Kaiser 窗获得最小阶设计。即使 Kaiser 窗方法对相同设定产生更大的滤波器阶数，当设计设定非常严格时，该算法的计算成本更低，并且不太可能出现收敛问题。如果应用需要非常窄的过渡带宽度或非常大的阻带衰减，就可能出现这种情况。

使用 Kaiser 窗方法设计与上述设定相同的滤波器，并将其响应与等波纹滤波器进行比较。

dk = designfilt（‘lowpassfir’，‘PassbandFrequency’，Fpass，。..

‘StopbandFrequency’，Fstop，‘PassbandRipple’，Ap，。..

‘StopbandAttenuation’，Ast， ‘DesignMethod’， ‘kaiserwin’）;

addfilter（hfvt，dk）;

legend（hfvt，‘Equiripple design’， ‘Kaiser window design’）

N = filtord（dk）

N = 52

3 以赫兹为单位指定频率参数

如果知道滤波器工作将使用的采样率，可以指定采样率和频率（以赫兹为单位）。重新设计采样率为 2 kHz 的最小阶等波纹滤波器。

Fpass = 370;

Fstop = 430;

Ap = 1;

Ast = 30;

Fs = 2000;

d = designfilt（‘lowpassfir’，‘PassbandFrequency’，Fpass，。..

‘StopbandFrequency’，Fstop，‘PassbandRipple’，Ap，。..

‘StopbandAttenuation’，Ast，‘SampleRate’，Fs）;

hfvt = fvtool（d）;

4 固定阶、固定过渡带宽度

固定阶设计适用于对计算负载敏感或对滤波器系数个数有限制的应用。一种选择是以控制通带波纹/阻带衰减为代价来固定过渡带宽度。

假设一个 30 阶低通 FIR 滤波器，其通带频率为 370 Hz，阻带频率为 430 Hz，采样率为 2 kHz。对于这组特定设定，可使用两种设计方法：等波纹法和最小二乘法。下面我们为每种方法设计一个滤波器，并比较结果。

N = 30;

Fpass = 370;

Fstop = 430;

Fs = 2000;

% Design method defaults to ‘equiripple’ when omitted

deq = designfilt（‘lowpassfir’，‘FilterOrder’，N，‘PassbandFrequency’，Fpass，。..

‘StopbandFrequency’，Fstop，‘SampleRate’，Fs）;

dls = designfilt（‘lowpassfir’，‘FilterOrder’，N，‘PassbandFrequency’，Fpass，。..

‘StopbandFrequency’，Fstop，‘SampleRate’，Fs，‘DesignMethod’，‘ls’）;

hfvt = fvtool（deq，dls）;

legend（hfvt，‘Equiripple design’， ‘Least-squares design’）

等波纹滤波器非常适合必须满足特定容差的应用，例如设计具有给定最小阻带衰减或给定最大通带波纹的滤波器。另一方面，如果我们想最小化通带/阻带中（理想滤波器和实际滤波器之间）的误差能量，这些设计可能并不理想。

如果您要尽可能降低某个频带内信号的能量，请使用最小二乘设计。

在上述示例中，设计的滤波器在通带和阻带中具有相同的波纹。我们可以使用权重来减少其中一个频带内的波纹，同时保持滤波器阶数固定。例如，如果您希望阻带波纹是通带波纹的十分之一，则为阻带赋予的权重必须是通带权重的十倍。根据上述情况重新设计等波纹滤波器。

deqw = designfilt（‘lowpassfir’，‘FilterOrder’，N，‘PassbandFrequency’，Fpass，。..

‘StopbandFrequency’，Fstop，‘SampleRate’，Fs，。..

‘PassbandWeight’，1，‘StopbandWeight’，10）;

hfvt = fvtool（deq，deqw）;

legend（hfvt，‘Equiripple design’， ‘Equiripple design with weighted stopband’）

5 固定阶、固定截止频率

可以使用窗口设计方法设计具有固定滤波器阶数和截止频率的滤波器。

可以使用不同窗口来控制阻带衰减，同时保持滤波器阶数不变。

例如，假设有截止频率为 60 Hz、采样率为 1 kHz 的 100 阶低通 FIR 滤波器。比较使用 Hamming 窗和使用旁瓣衰减为 90 dB 的 Chebyshev 窗产生的设计。

dhamming = designfilt（‘lowpassfir’，‘FilterOrder’，100，‘CutoffFrequency’，60，。..

‘SampleRate’，1000，‘Window’，‘hamming’）;

dchebwin = designfilt（‘lowpassfir’，‘FilterOrder’，100，‘CutoffFrequency’，60，。..

‘SampleRate’，1000，‘Window’，{‘chebwin’，90}）;

hfvt = fvtool（dhamming，dchebwin）;

legend（hfvt，‘Hamming window’， ‘Chebyshev window’）

可以通过其他方式指定具有固定阶数的滤波器：固定截止频率、通带波纹和阻带衰减；固定过渡带宽度；以及固定半功率 （3dB） 频率。

责任编辑：haq