

一个线性稳压器阶跃响应的测试数据示例
描述
线性稳压器的稳定性优化简易方法
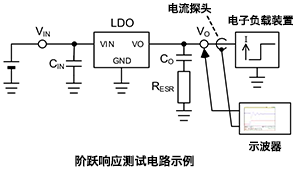
在上一篇文章,我们介绍了线性稳压器阶跃响应的测试方法和具体的线性稳压器阶跃响应电路。本文将介绍一个线性稳压器阶跃响应的测试数据示例。
阶跃响应波形示例
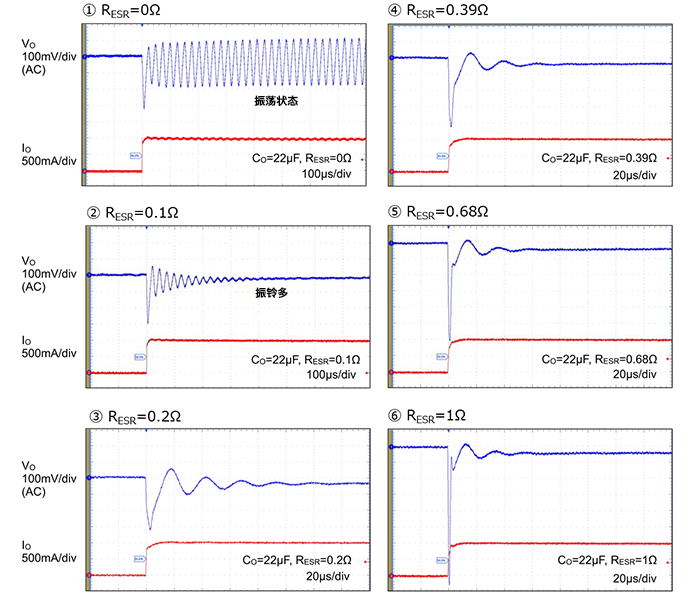
下面的波形图是使电路图中的RESR从0Ω~1Ω变化时的阶跃响应(负载瞬态响应)示例。
(点击查看大图)
①是RESR为0Ω,即未添加的状态。当负载电流上升时,输出振荡。这是使用MLCC作为输出电容器时发生振荡现象的一个示例。从相位的角度来看,几乎没有裕度。
②是RESRを0.1Ω时的波形。发生振铃并逐渐收敛,但是到稳定所花的时间很长,并且振铃可能会作为噪声产生不利影响。
③是RESR为0.2Ω时的波形。振铃大大减少。请注意,从③开始的时间轴为20µs/div。
之后的波形中,当将RESR增加到1Ω时,振铃会略有减少,但响应变慢,并且在负载上升的时间点,输出电压的下降幅度增加。
在这6个示例中,可以看出③或④、或介于两者之间的RESR值是折衷值。
有一些注意事项。在该示例中,CO为22µF,但如果CO的电容量变化,特性也会变化。在进行优化时,可能还需要考虑电容量。另外,还有其他一些影响因素,比如负载电流值、电流阶跃的压摆率、线性稳压器IC的类型等。因此,难以一概而论地确定常数,而且在这个电路条件下找到的最佳常数也不一定适用于其他电路。示例中的电阻值只是一个类似于切入点的参考,实际上还需要考虑其他条件。
(点击查看大图)
关键要点
・当无法测量线性稳压器相位裕度时,解决方案之一是使用阶跃响应法轻松地确认线性稳压器的稳定性。
・从线性稳压器阶跃响应的观察波形中,找出振铃较小、收敛较快的常数。
・可以说线性稳压器阶跃响应特性是基于多种因素的综合特性,因此在进行优化时不是只确认一个部件的常数,还要确认其他部件的参数。
编辑:jq
-
线性稳压器的稳定性优化简易方法-阶跃响应波形和相关部件常数2023-02-23 1102
-
什么是线性稳压器?2022-04-18 6671
-
线性稳压器选型和设计的5个因素2021-07-07 2658
-
线性稳压器的特性2021-02-20 4431
-
关于线性稳压器的五个设计细节2020-11-17 4093
-
负电压线性稳压器2018-10-11 4296
-
线性稳压器与开关稳压器的联系和区别2018-10-09 3677
-
线性稳压器与开关稳压器有什么不同2018-09-29 4675
-
选择保障线性稳压器稳定度的ESR2018-08-31 1521
-
线性稳压器的类别2018-02-11 5166
-
线性稳压器,线性稳压器的结构原理是什么?2010-03-23 2272
全部0条评论

快来发表一下你的评论吧 !

