

DeepMind如何用神经网络自动构建启发式算法
电子说
描述
混合整数规划(MIP)是一类 NP 困难问题,来自 DeepMind、谷歌的一项研究表明,用神经网络与机器学习方法可以解决混合整数规划问题。
混合整数规划(Mixed Integer Program, MIP)是一类 NP 困难问题,旨在最小化受限于线性约束的线性目标,其中部分或所有变量被约束为整数值。混合整数规划的形式如下:
MIP 已经在产能规划、资源分配和装箱等一系列问题中得到广泛应用。人们在研究和工程上的大量努力也研发出了 SCIP、CPLEX、Gurobi 和 Xpress 等实用的求解器。这些求解器使用复杂的启发式算法来指导求解 MIP 的搜索过程,并且给定应用上求解器的性能主要依赖于启发式算法适配应用的程度。
在本文中,来自 DeepMind、谷歌的研究者展示了机器学习可以用于从 MIP 实例数据集自动构建有效的启发式算法。
在实践中经常会出现这样的用例,即应用程序需要用不同的问题参数解决同一高级语义问题的大量实例。
文中此类「同质」数据集的示例包括:(1)优化电网中发电厂的选择以满足需求,其中电网拓扑保持不变,而需求、可再生能源发电等则因情况而异(2)解决了谷歌在生产系统中的一个包装问题,在这个系统中,要包装的「items」和「bins」的语义基本保持不变,但它们的尺寸在不同的实例之间有所波动。
然而,现有的 MIP 求解器无法自动构造启发式来利用这种结构。在具有挑战性的应用程序中,用户可能依赖专家设计的启发式,或者以放弃潜在的大型性能改进为代价。而机器学习提供了在不需要特定于应用程序专业知识的情况下进行大规模改进的可能性。
论文地址:https://arxiv.org/pdf/2012.13349.pdf
该研究证明,机器学习可以构建针对给定数据集的启发式算法,其性能显著优于 MIP 求解器中使用的经典算法,特别是具有 SOTA 性能的非商业求解器 SCIP 7.0.1。
该研究将机器学习应用于 MIP 求解器的两个关键子任务:(1)输出对满足约束的所有变量的赋值(如果存在此类赋值)(2)证明变量赋值与最优赋值之间的目标值差距边界。这两个任务决定了该方法的主要组件,即:Neural Diving、 Neural Branching。
该研究在不同的数据集上进行了评估,这些数据集包含来自实际应用的大规模 MIP,包括来自谷歌生产系统和 MIPLIB 的两组数据。来自所有数据集的大多数 MIP 组合集在解算后都有 10^3-10^6 个变量和约束,这明显大于早期的工作。
一旦在给定的数据集上训练 Neural Diving 和 Neural Branching 模型,它们就被集成到 SCIP 中,以形成专门针对该数据集的「神经求解器」。基线是 SCIP,其重点参数通过网格搜索在每个数据集上进行调整,称之为 Tuned SCIP。
将神经求解器和 Tuned SCIP 与原始对偶间隙(primal-dual gap)在一组实例上的平均值进行比较,图 2 所示,神经求解器在相同的运行时间内提供了更好的间隙,或者在更短的时间内提供了相同的间隙,在五个数据集中进行评估,有四个数据集的 MIP 最大,而第五个数据集的性能与 Tuned SCIP 性能相匹配。据了解,这是第一次使用机器学习在大规模真实应用数据集和 MIPLIB 上得到如此大的改进。
MIP 表示与神经网络架构
该研究描述了 MIP 如何表示为神经网络的输入,并用来学习 Neural Diving、Neural Branching 模型的架构。该研究使用的深度学习架构为一种图神经网络,特别是图卷积网络 (GCN)。
将 MIP 表示为神经网络的输入
该研究使用 MIP 的二部图表示,方程(1)可用于定义二部图,其中图中的一组 n 个节点对应于被优化的 n 个变量,另一组 m 个节点对应于 m 个约束。
神经网络架构
下面介绍一下 Neural Diving 、 Neural Branching 所使用的网络架构中共同的方面。
给定一个 MIP 的二部图表示,该研究使用 GCN 来学习 Neural Diving 、Neural Branching 模型。设 GCN 的输入为图,其中 V 为节点集合、ε为边集合、A 为图邻接矩阵。对于 MIP 二部图,V 是 n 个变量节点和 m 个约束节点的并集,大小 N := |V| = n + m。一个单层 GCN 用来学习计算输入图中每个节点的 H 维连续向量表示,称为节点嵌入。
在 MIP 和 GCN 体系架构中二部图表示的两个关键性质是:(1)网络输出对变量和约束的排列是不变的(2)可以使用同一组参数应用于不同大小的 MIP。
这两个性质很重要,因为变量和约束可能没有任何规范顺序,而且同一应用程序中的不同实例可能具有不同数量的变量和约束。
架构改进
该研究对上述体系架构进行了改进,这些改进提高了网络的性能,主要体现在以下方面:
该研究修改了 MIP 二部图的邻接矩阵 A ,以包含来自 MIP 约束矩阵 A 的系数,而不在是表示边缘存在的二进制值;
该研究通过连接来自第 l 层的节点嵌入来扩展第 l + 1 层的节点嵌入;该研究在每一层的输出处应用 layer norm,使得 Z^ (l+1) =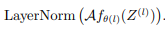
此外,该研究还探索了可以用来替代的架构,这些架构对节点和边使用嵌入,并使用单独的 MLP 来计算。当在每一层中使用具有高维边嵌入的此类网络时,它们的内存使用量可能会比 GCN 高得多,因为 GCN 只需要邻接矩阵,可能不适合 GPU 内存,除非以精度为代价减少层数。GCN 更适合扩展到大规模 MIP。
数据集
表 1 中总结了数据集的详细信息,除 MIPLIB 之外的所有数据集都是特定于应用程序的,即它们只包含来自单个应用程序的实例。
除了 MIPLIB 之外的所有数据集,该研究将实例随机拆分为 70%、15% 和 15% 的不相交子集来定义训练集、验证集和测试集。对于 MIPLIB,该研究使用来自 MIPLIB 2017 基准集的实例作为测试集。
在删除与 MIPLIB 2017 基准集的重叠实例后,分别使用 MIPLIB 2017 Collection Set 和 MIPLIB 2010 set 作为训练集和验证集。对每个数据集来说,训练集用于学习该数据集的模型,验证集用于调整学习超参数和 SCIP 的元参数,测试集用于报告评估结果。
评估
首先该研究单独评估了 Neural Diving、 Neural Branching,后续又进行了联合评估。不管在哪种情况下,该研究都评估了与训练集分离的 MIP 测试集,以衡量模型对未见实例的泛化能力。并使用 gap plot 和 survival plot 呈现结果。
校准时间(Calibrated time):所有数据集和比较任务所需的评估工作量需要 160000 多个 MIP 解算,以及近一百万个 CPU 和 GPU 小时。为了满足计算需求,该研究使用了一个共享的、异构的计算集群。
为了提高准确性,对于每个求解任务,该研究定期在同一台机器上的不同线程上解决一个小的校准 MIP。该研究还使用在同一台机器上解决任务时的校准 MIP 求解数的估计来测量时间,然后使用参考机器上的校准 MIP 求解时间将这个量转换为时间值。
Neural Diving
在本节中,研究者用本文方法来学习 diving-style 原始启发式的方法,该算法从给定的实例分布为 MIP 生成高质量的赋值。思想是训练一个生成模型,对 MIP 的整数变量进行赋值,从这些整数变量中可以抽样部分赋值。该研究使用 SCIP 获得高质量的赋值(不一定是最优的)作为 MIP 训练集的目标标签。
一旦在这些数据上进行了训练,该模型就可以预测来自同一问题分布的未见实例上的整数变量值。模型预测中所表示的不确定性被用于定义对原始 MIP 的部分赋值,该初始 MIP 固定了很大一部分整型变量。这些非常小的 sub-MIP 可以使用 SCIP 快速解决,产生高质量的可行赋值。
解决方案预测作为条件生成模型
考虑一个整数程序(即,所有变量都是整数),其参数为 M = (A, b, c)(见方程 1),并在一组整数变量 x 上有一个非空可行集。假设最小化,该研究使用目标函数定义 x 上的一个能量函数:
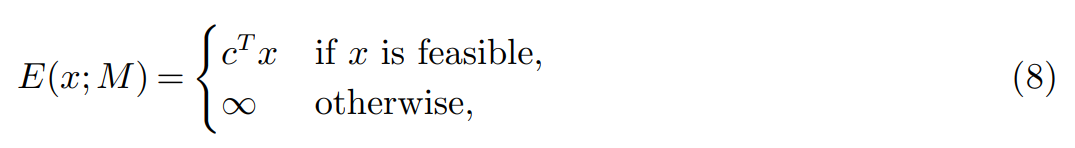
注意,所有变量都使用了相同的 MLP
模型预测与经典求解器相结合
该研究使用 SelectiveNet 方法训练了一个额外的二元分类器,可以用来判断哪些变量需要预测,哪些不需要预测,并优化变量之间的「coverage」,将其定义为预测变量数与未预测变量数之比。
通过分配或收紧大部分变量的边界,该研究显著地减少了问题的规模,并热启动 SCIP,以在更短的时间内找到高质量的解决方案。
这种方法还提供了实际的计算优势:预测抽样和解搜索是完全并行的。研究者可以重复和独立地从模型中提取不同的样本,并且样本的每个部分赋值都可以独立地求解。
结果
该研究在训练集上为每个数据集训练一个 GNN,并在验证集上调整超参数。 原始间隙(primal gap)与基线 SCIP 的平均结果。
与 SCIP 相比,该研究在并行和顺序运行方面,在所有数据集上以更短的时间产生更好的原始边界。研究者认为该方法的优势是能迅速找到好的解决方案,但有时它不能找到最优或接近最优的解决方案。这可以从图 7 的 survival plot 中看出,Neural Diving 方法在较短的时间限制下胜出,但在 Electric Grid Optimization 和 MIPLIB 数据集上不如 SCIP。
该研究在两个数据集上(Google Production Packing 、 NN Verification,如图 8、9 所示)引入了两个额外的结果,并且将 Neural Diving、Gurobi 求解器进行结合:该研究以同样的方式分配变量,但使用 Gurobi 而不是 SCIP 来解决剩下的问题。
除了在上表 1 中的数据集上评估 Neural Diving 之外,研究者还通过修改自身方法来求解 MIPLIB 2017 Collection Set 中的开放实例。这些实例是 MIPLIB 2017 Collection Set 能够提供的 hardest 的问题。
Neural Branching
分支定界(branch-and-bound)过程在每次迭代时需要做出两个决策,即扩展哪个叶节点以及在哪个变量上分支。研究者专注于后一个决策。变量选择决策的质量对求解 MIP 时分支定界所采取的步骤数量具有重大影响。通过模拟节点高效但计算昂贵的 expert 的行动,他们使用深度神经网络来学习变量选择策略。
通过将昂贵 expert 的策略提炼到神经网络中,研究者寻求保持大致相同的决策质量,但大大减少了做出决策所需时间。给定树节点的决策完全是该节点的本地决策,因此学习策略只需要将节点的表示而不是整个树作为输入,由此实现更强的可扩展性。
为了证明 expert 数据生成的可扩展性得到了提升,研究者将 ADMM expert 与 Gasse 等人于 2019 年使用的 expert,即 Google Production Packing 和 MIPLIB 上的 Vanilla Full Strong Branching (VFSB)进行了比较。
模仿学习是给定 expert 行为示例的情况时寻求学习 expert 策略的算法的统称。研究者在本文中将模仿学习表述为一个监督学习问题,并考虑了三种变体:克隆 expert 策略、随机移动的蒸馏和 DAgger。
在实验中,研究者将他们选择的三种模仿学习变体作为超参数对每个数据集进行调整。他们使用这三种变体为每个数据集生成了数据和训练策略,并选定了三小时内在验证集实例上取得最低平均对偶间隙(dual gap)的策略,接着在测试集上对选定的策略进行评估以得出相关结果。
结果
研究者在优化双重约束的任务上对学得的分支策略进行评估。下图 展示了 Neural Branching 与 Tuned SCIP 的平均对偶间隙曲线图:
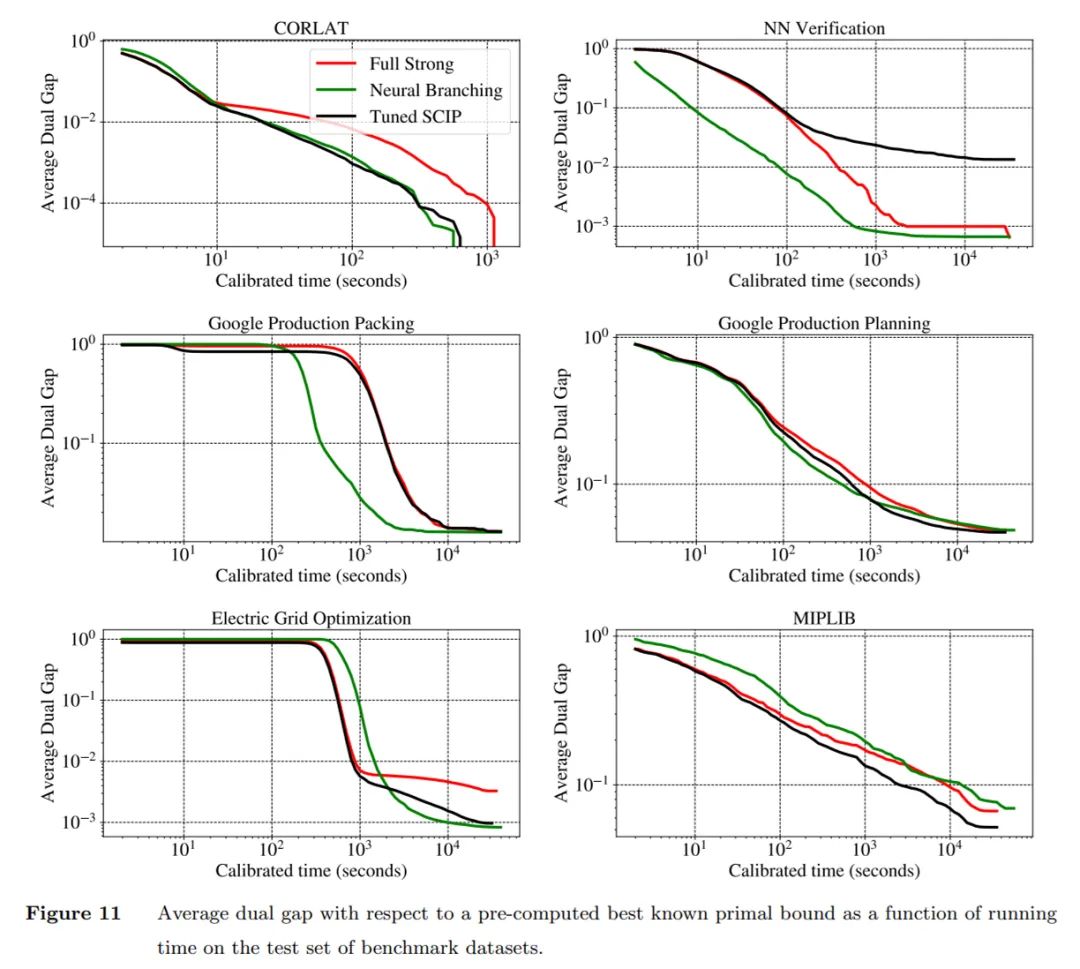
将一个数据集的目标最优间隙应用于每个测试集 MIP 实例的对偶间隙时计算得出的生存曲线。研究者确认了上图 得出的结论,即在除 Google Production Planning 和 MIPLIB 之外的所有数据集上,Neural Branching 能够在所有时间期限内持续地求解出更高分数的测试实例。
联合评估
研究者将 Neural Branching 和 Neural Diving 结合成了单个求解器,这种做法使得在 Tuned SCIP 上实现了显著加速。他们通过 PySCIPOpt 包提供的接口使用并将学得的启发式方法集成到 SCIP 中。
此外,研究者考虑了四种结合 Neural Branching 和 Neural Diving 的可能方法,具体如下:
单独的 Tuned SCIP;
Neural Branching+Neural Diving(序列)使用神经启发式方法;
Neural Branching 仅使用学得的 branching 策略;
Tuned SCIP+Neural Diving(序列)仅使用连续版本的 Neural Diving。
作为运行时间函数的平均原始对偶间隙曲线,神经求解器在四个数据集上显著优于 Tuned SCIP。
具体来讲,在 NN Verification 数据集上,神经求解器在大的时间期限内平均原始对偶间隙比 Tuned SCIP 好 5 个数量级以上;在 Google Production Packing 数据集上,Neural Branching 和 Neural Diving(序列)更快地实现更低的间隙,在比 Tuned SCIP 时间少 5 倍多的情况下达到了 0.1 的间隙,但 Tuned SCIP 最后赶上了;在 Electric Grid Optimization 数据集上,神经求解器以更高的运行时间实现了低一半的间隙;在 MIPLIB 数据集上,Tuned SCIP+Neural Diving(序列)组合以更高的运行时间实现了 1.5 倍的间
研究者进一步确认了观察结果,同样在四个数据集上,神经求解器在给定时间期限内求解测试集问题时能够取得比 Tuned SCIP 更高的分数。因此,这些结果表明学习可以显著提升 SCIP 等强大求解器的性能。
编辑:jq
-
基于神经网络算法的模型构建方法2024-07-02 1578
-
构建神经网络模型的常用方法 神经网络模型的常用算法介绍2023-08-28 1492
-
量子启发式提升投资收益:指数复制与指数优化2022-11-01 1856
-
如何构建神经网络?2021-07-12 1861
-
基于启发式搜索算法的无人机航迹规划2021-07-02 804
-
启发式算法和遗传混合算法在流水车间的应用2021-06-30 733
-
改进的双向启发式搜索算法主要流程是怎样的?2021-05-17 1849
-
反馈神经网络算法是什么2020-04-28 2885
-
【案例分享】基于BP算法的前馈神经网络2019-07-21 3238
-
基于区分对象集的启发式属性约简算法2018-01-05 792
-
基于网页排名算法面向论文索引排名的启发式方法2017-12-30 738
-
关于HTSM(启发式策略模型)的详细介绍2016-05-19 1967
-
基于粗糙集的启发式约简算法2009-10-19 530
-
混合启发式算法在汽车调度中的应用2009-09-19 3177
全部0条评论

快来发表一下你的评论吧 !

