线性分组码,线性分组码是什么意思

线性分组码,线性分组码是什么意思

分组码是一组固定长度的码组，可表示为（n , k），通常它用于前向纠错。在分组码中，监督位被加到信息位之后，形成新的码。在编码时，k个信息位被编为n位码组长度，而n-k个监督位的作用就是实现检错与纠错。当分组码的信息码元与监督码元之间的关系为线性关系时，这种分组码就称为线性分组码。

对于长度为n的二进制线性分组码，它有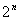种可能的码组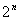，从种码组中，可以选择M=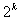个码组（k个码组构成的码集中选出来的，这样剩下的码组就可以对这个分组码进行检错或纠错。

线性分组码是建立在代数群论基础之上的，各许用码的集合构成了代数学中的群，它们的主要性质如下：

（1）任意两许用码之和（对于二进制码这个和的含义是模二和）仍为一许用码，也就是说，线性分组码具有封闭性；

（2）码组间的最小码距等于非零码的最小码重。

在8.2.1节中介绍的奇偶监督码，就是一种最简单的线性分组码，由于只有一位监督位通常可以表示为（n,n-1），式（1）表示采用偶校验时的监督关系。在接收端解码时，实际上就是在计算：

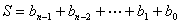（2）

其中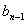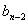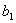， …表示接收到的信息位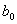，表示接收到的监督位，若S＝0，就认为无错；若S＝1就认为有错。式（2）被称为监督关系式，S是校正子。由于校正子S的取值只有“0”和“1”两种状态，因此，它只能表示有错和无错这两种信息，而不能指出错码的位置。

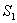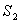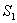
设想如果监督位增加一位，即变成两位，则能增加一个类似于式（2）的监督关系式，计算出两个校正子和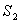， 而共有4种组合：00，01，10，11，可以表示4种不同的信息。除了用00表示无错以外，其余3种状态就可用于指示3种不同的误码图样。

同理，由r个监督方程式计算得到的校正子有r位，可以用来指示 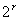-1种误码图样。对于一位误码来说，就可以指示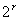-1个误码位置。对于码组长度为n、信息码元为k位、监督码元为r＝n - k位的分组码（常记作（n，k）码），如果希望用r个监督位构造出r个监督关系式来指示一位错码的n种可能，则要求：

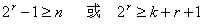(3)

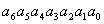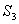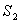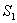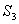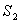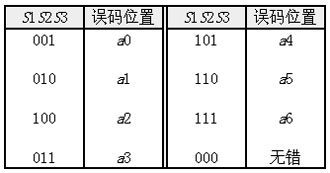
下面通过一个例子来说明线性分组码是如何构造的。设分组码（n , k）中k = 4，为了能够纠正一位错误，由式（3）可以看到，要求r ≥ 3，若取r = 3，则n = k+r = 7。因此，可以用表示这7个码元，用、、表示利用三个监督方程，通过计算得到的校正子，并且假设、 、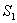三位校正字码组与误码位置的关系如表1（当然，也可以规定成另一种对应关系，这并不影响讨论的一般性）：

由表中规定可已看到，仅当一错码位置在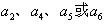时，校正子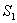为1；否则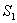为0。这就意味着 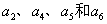四个码元构成偶数监督关系：

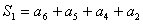(4a)

同理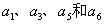，构成偶数监督关系：

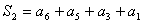（4b）

表1校正字与误码位置

以及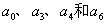构成有数监督关系：

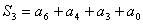（4c）

在发送端编码时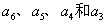是信息码元，它们的值取决于输入信号，因此是随机的。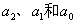是监督码元，它们的取值由监督关系来确定，即监督位应使式（4）的三个表达式中的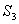、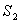和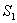的值为零（表示编成的码组中应无错码），这样式（4）的三个表达式可以表示成下面的方程组形式：

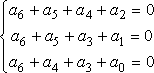（5）

由上式经移项运算，接出监督位

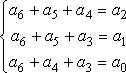（6）

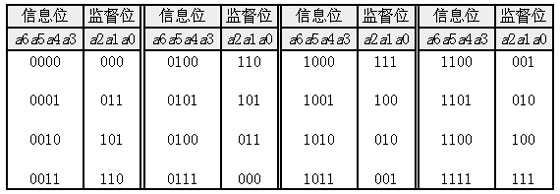
根据上面两个线性关系，可以得到16个许用码组如表2所示：

表2许用码组

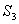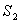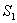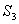
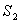
接收端收到每个码组后，计算出 、和，如不全为0，则可按表8-4确定误码的位置，然后予以纠正。例如，接收码组为0000011，可算出 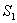＝011，由表8-4可知在 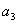位置上有一误码。

不难看出，上述（7，4）码的最小码距，因此，它能纠正一个误码或检测两个误码。如超出纠错能力，则反而会因“乱纠”而增加新的误码。