

C++基础语法十大排序算法后五个分享
描述
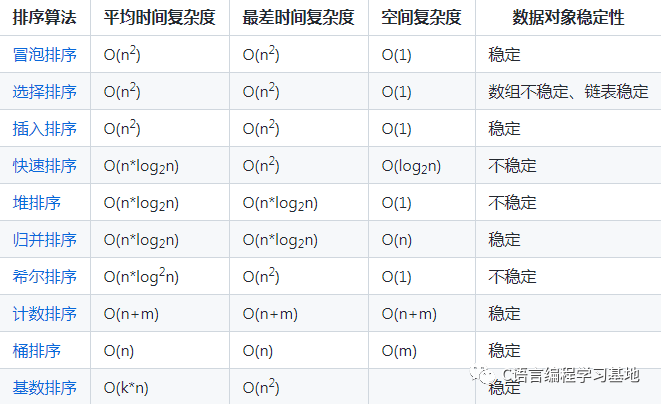
本期是C++基础语法分享的第十六节,今天给大家来梳理一下十大排序算法后五个!
归并排序
归并排序:把数据分为两段,从两段中逐个选最小的元素移入新数据段的末尾。可从上到下或从下到上进行。
/***************** 迭代版*****************
///整數或浮點數皆可使用,若要使用物件(class)時必須設定“小於”(《)的運算子功能template《typename T》void merge_sort(T arr[], int len) { T* a = arr;
T* b = new T[len]; for (int seg = 1;
seg 《 len; seg += seg) { for (int start = 0; start 《 len; start += seg + seg) { int low = start, mid = min(start + seg, len), high = min(start + seg + seg, len);
int k = low; int start1 = low, end1 = mid; int start2 = mid, end2 = high; while (start1 《 end1 && start2 《 end2) b[k++] = a[start1] 《 a[start2] ? a[start1++] : a[start2++]; while (start1 《 end1) b[k++] = a[start1++];
while (start2 《 end2) b[k++] = a[start2++]; } T* temp = a;
a = b; b = temp; } if (a != arr) { for (int i = 0; i 《 len; i++) b[i] = a[i]; b = a;
} delete[] b;}
/***************** 递归版*****************/template《typename T》void merge_sort_recursive(T arr[], T reg[], int start, int end) { if (start 》= end) return; int len = end - start, mid = (len 》》 1) + start; int start1 = start, end1 = mid;
int start2 = mid + 1, end2 = end; merge_sort_recursive(arr, reg, start1, end1); merge_sort_recursive(arr, reg, start2, end2);
int k = start; while (start1 《= end1 && start2 《= end2) reg[k++] = arr[start1] 《 arr[start2] ? arr[start1++] : arr[start2++];
while (start1 《= end1) reg[k++] = arr[start1++]; while (start2 《= end2) reg[k++] = arr[start2++];
for (k = start; k 《= end; k++) arr[k] = reg[k];}//整數或浮點數皆可使用,若要使用物件(class)時必須設定“小於”(《)的運算子功能template《typename T》 void merge_sort(T arr[], const int len) { T *reg = new T[len]; merge_sort_recursive(arr, reg, 0, len - 1); delete[] reg;}
希尔排序
希尔排序:每一轮按照事先决定的间隔进行插入排序,间隔会依次缩小,最后一次一定要是1。
template《typename T》void shell_sort(T array[], int length) { int h = 1; while (h 《 length / 3) { h = 3 * h + 1; } while (h 》= 1) { for (int i = h; i 《 length; i++) { for (int j = i; j 》= h && array[j] 《 array[j - h]; j -= h) { std::swap(array[j], array[j - h]); } } h = h / 3; }}
计数排序
计数排序:统计小于等于该元素值的元素的个数i,于是该元素就放在目标数组的索引i位(i≥0)。
计数排序基于一个假设,待排序数列的所有数均为整数,且出现在(0,k)的区间之内。
如果 k(待排数组的最大值) 过大则会引起较大的空间复杂度,一般是用来排序 0 到 100 之间的数字的最好的算法,但是它不适合按字母顺序排序人名。
计数排序不是比较排序,排序的速度快于任何比较排序算法。
时间复杂度为 O(n+k),空间复杂度为 O(n+k)
算法的步骤如下:
1. 找出待排序的数组中最大和最小的元素
2. 统计数组中每个值为 i 的元素出现的次数,存入数组 C 的第 i 项
3. 对所有的计数累加(从 C 中的第一个元素开始,每一项和前一项相加)
4. 反向填充目标数组:将每个元素 i 放在新数组的第 C[i] 项,每放一个元素就将 C[i] 减去 1
#include 《iostream》#include 《vector》#include 《algorithm》
using namespace std;
// 计数排序void CountSort(vector《int》& vecRaw, vector《int》& vecObj){ // 确保待排序容器非空 if (vecRaw.size() == 0) return;
// 使用 vecRaw 的最大值 + 1 作为计数容器 countVec 的大小 int vecCountLength = (*max_element(begin(vecRaw), end(vecRaw))) + 1; vector《int》 vecCount(vecCountLength, 0);
// 统计每个键值出现的次数 for (int i = 0; i 《 vecRaw.size(); i++) vecCount[vecRaw[i]]++; // 后面的键值出现的位置为前面所有键值出现的次数之和 for (int i = 1; i 《 vecCountLength; i++) vecCount[i] += vecCount[i - 1];
// 将键值放到目标位置 for (int i = vecRaw.size(); i 》 0; i--) // 此处逆序是为了保持相同键值的稳定性 vecObj[--vecCount[vecRaw[i - 1]]] = vecRaw[i - 1];}
int main(){ vector《int》 vecRaw = { 0,5,7,9,6,3,4,5,2,8,6,9,2,1 }; vector《int》 vecObj(vecRaw.size(), 0);
CountSort(vecRaw, vecObj);
for (int i = 0; i 《 vecObj.size(); ++i) cout 《《 vecObj[i] 《《 “ ”; cout 《《 endl;
return 0;}
桶排序
桶排序:将值为i的元素放入i号桶,最后依次把桶里的元素倒出来。
桶排序序思路:
1. 设置一个定量的数组当作空桶子。
2. 寻访序列,并且把项目一个一个放到对应的桶子去。
3. 对每个不是空的桶子进行排序。
4. 从不是空的桶子里把项目再放回原来的序列中。
假设数据分布在[0,100)之间,每个桶内部用链表表示,在数据入桶的同时插入排序,然后把各个桶中的数据合并。
const int BUCKET_NUM = 10;
struct ListNode{ explicit ListNode(int i=0):mData(i),mNext(NULL){} ListNode* mNext; int mData;};
ListNode* insert(ListNode* head,int val){ ListNode dummyNode; ListNode *newNode = new ListNode(val); ListNode *pre,*curr; dummyNode.mNext = head; pre = &dummyNode; curr = head; while(NULL!=curr && curr-》mData《=val){ pre = curr; curr = curr-》mNext; } newNode-》mNext = curr; pre-》mNext = newNode; return dummyNode.mNext;}
ListNode* Merge(ListNode *head1,ListNode *head2){ ListNode dummyNode; ListNode *dummy = &dummyNode; while(NULL!=head1 && NULL!=head2){ if(head1-》mData 《= head2-》mData){ dummy-》mNext = head1; head1 = head1-》mNext; }else{ dummy-》mNext = head2; head2 = head2-》mNext; } dummy = dummy-》mNext; } if(NULL!=head1) dummy-》mNext = head1; if(NULL!=head2) dummy-》mNext = head2; return dummyNode.mNext;}
void BucketSort(int n,int arr[]){ vector《ListNode*》 buckets(BUCKET_NUM,(ListNode*)(0)); for(int i=0;i《n;++i){ int index = arr[i]/BUCKET_NUM; ListNode *head = buckets.at(index); buckets.at(index) = insert(head,arr[i]); } ListNode *head = buckets.at(0); for(int i=1;i《BUCKET_NUM;++i){ head = Merge(head,buckets.at(i)); } for(int i=0;i《n;++i){ arr[i] = head-》mData; head = head-》mNext; }}
基数排序
基数排序:一种多关键字的排序算法,可用桶排序实现。
int maxbit(int data[], int n) //辅助函数,求数据的最大位数{ int maxData = data[0]; ///《 最大数 /// 先求出最大数,再求其位数,这样有原先依次每个数判断其位数,稍微优化点。 for (int i = 1; i 《 n; ++i) { if (maxData 《 data[i]) maxData = data[i];
} int d = 1;
int p = 10; while (maxData 》= p) { //p *= 10; // Maybe overflow maxData /= 10; ++d; } return d;/* int d = 1; //保存最大的位数 int p = 10; for(int i = 0; i 《 n; ++i) { while(data[i] 》= p) { p *= 10; ++d;
} } return d;*/}void radixsort(int data[], int n) //基数排序{ int d = maxbit(data, n);
int *tmp = new int[n]; int *count = new int[10];
//计数器 int i, j, k; int radix = 1; for(i = 1; i 《= d; i++) //进行d次排序 { for(j = 0; j 《 10; j++) count[j] = 0; //每次分配前清空计数器 for(j = 0; j 《 n; j++) { k = (data[j] / radix) % 10; //统计每个桶中的记录数 count[k]++; } for(j = 1; j 《 10; j++) count[j] = count[j - 1] + count[j];
//将tmp中的位置依次分配给每个桶 for(j = n - 1; j 》= 0; j--) //将所有桶中记录依次收集到tmp中 { k = (data[j] / radix) % 10; tmp[count[k] - 1] = data[j];
count[k]--; } for(j = 0; j 《 n; j++) //将临时数组的内容复制到data中 data[j] = tmp[j]; radix = radix * 10;
} delete []tmp; delete []count;}
今天的分享就到这里了,大家要好好学C++哟~
责任编辑:haq
-
Matlab数学建模常用的十大算法2012-05-20 20811
-
C语言十大滤波算法2012-08-15 8143
-
Java常用排序算法&程序员必须掌握的8大排序算法+二分法查找2015-10-19 2861
-
《Visual C# 2008程序设计经典案例设计与实现》---利用冒泡算法实现从小到大排序2017-05-22 2557
-
经典算法大全(51个C语言算法+单片机常用算法+机器学十大算法)2018-10-23 42699
-
C语言教程之3个数由小到大排序2016-04-22 413
-
汽车led大灯十大排名2017-12-13 218706
-
数据结构常见的八大排序算法2018-02-05 1951
-
C++语法的外围基础2018-03-15 791
-
程序员的内功:C语言八大排序算法2020-10-26 2667
-
C++中十大排序算法前五个详解2021-09-29 1969
-
C语言动图演示十大经典排序算法(含代码)2023-01-29 1973
-
C语言经典排序算法总结2023-06-05 918
-
单片机ADC,十大C语言滤波算法2023-10-24 2050
-
十大排序算法总结2023-12-20 1969
全部0条评论

快来发表一下你的评论吧 !

