FIR数字滤波器的FPGA实现研究策略

FIR数字滤波器的FPGA实现研究策略

  如今，FPGA已成为数字信号处理系统的核心器件，尤其在数字通信、网络、视频和图像处理等领域。现在的FPGA不仅包含查找表、寄存器、多路复用器、分布式块存储器，而且还嵌入专用的快速加法器、乘法器和输入，输出设备。FPGA具有实现高速并行运算的能力，因而成为高性能数字信号处理的理想器件。此外，与专用集成电路(ASIC)相比，FPGA具有可重复编程的优点。
    根据单位脉冲响应的不同，数字滤波器主要分为有限脉冲响应(FIR)和无限脉冲响应(IIR)2大类。在同样的设计要求下，IIR方式计算工作量较小。但难以得到线性相位响应，且系统不易稳定；FIR方式的计算工作量稍大，但在设计任意幅频特性时，能保证严格的线性相位特性；由于其实现结构主要是非递归的，FlR滤波器可以稳定工作。FIR数字滤波器是数字多普勒接收机的重要组成部分，因此，研究FIR数字滤波器的实现技术具有重要意义。随着FPGA技术的不断发展，FPGA逐渐成为信号处理的主流器件。而在FPGA中，数字滤波器不同的实现方法所消耗的FPGA资源是不同的，且对滤波器的性能影响也有较大差异。

1 FIR滤波器的原理及结构
    FIR滤波器存在N个抽头的h(n)，N称为滤波器的阶数，其数学表达式为：
   
式中，x(k)为第k时刻的采样值，y(n)为滤波器输出。h(k)为FIR滤波器的第k级抽头系数。
    通过对h(k)进行Z变换得到FIR的传递函数H(Z)，其在Z域内的形式如下：
   
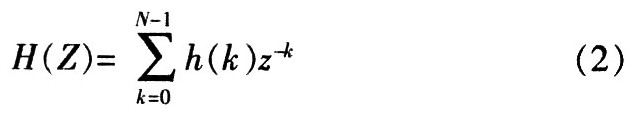
    因此，根据传递函数H(Z)和FIR滤波器系数的对称性，可得FIR滤波器的一般实现结构，如图1所示。

    从串行结构中可以看出，FIR滤波过程就是一个信号逐级延迟的过程，将各级延迟输出加权累加，得到滤波输出，其中最主要的运算是乘累加运算。FIR每完成一次滤波过程需要进行N次乘法和(N-1)次加法运算，N为滤波器的阶数。所以，滤波器的运算量完全取决于N的大小，当N很大时，延迟将非常长，无法实现高速信号处理。
    根据FIR数字滤波器的对称特性，可以先进行加法运算，然后对加法运算的结果进行串行乘累加运算，从而得到改进的串行结构。与串行结构相比，改进的滤波器完成一次滤波的时钟周期减半，乘累加次数减半，提高了处理速度，但同时要消耗更多的硬件资源。图1(b)为Ⅳ位偶数时改进的串行结构。与串行结构相似，滤波器的运算量完全取决于N的大小，当N很大时，延迟将非常长，无法实现高速信号处理。
    将串行结构展开，根据滤波器的信号流图用多个乘法器和加法器并行实现，得到FIR滤波器的并行实现结构，如图1(c)所示。并行滤波器的滤波速度快，一个时钟周期内完成一次滤波，但消耗大量的FPGA资源，如乘累加器，且器件的延迟较大，工作频率不宜太高。
    FPGA具有规整的内部逻辑阵列和丰富的连线资源，特别适合用于数字信号处理。但以前FPGA一般用于系统逻辑或时序控制，很少应用在信号处理方面。其原因主要是FPGA中缺乏实现乘法运算的有效结构。随着FPGA技术的不断发展，查找表(LUT)技术的应用有效地解决了这个问题，使FPGA在数字信号处理方面得到了广泛应用。

2 基于分布式算法的FIR滤波器的实现
2．1 分布式算法原理
    上世纪70年代Croisie提出了分布式算法DA(Distributed Arithmetic)，但由于其特别适合用FPGA实现，所以直到Xilinx公司在FPGA中使用查找表(LUT)后，DA才被广泛应用在FPGA求乘积和中。
    FIR的滤波输出y可以表示为输入x和系数h的内积：
   
    由上述推导可知，分布式算法是一种以实现乘加运算为目的的运算方法。它与传统实现乘加运算的先后顺序不同。分布式算法在完成乘加功能时，是通过将各输入数据每一对应位产生的部分积预先进行相加形成相应部分积，然后在对各部分积预先进行累加形成最终结果；而传统算法是等到所有乘积产生之后再进行相加来完成乘加运算。
2．2 分布式FIR的实现结构
    图2为分布式FIR滤波器的直接实现结构。对于小位宽的数据，DA算法不仅速度快，而且所占用的芯片资源少。

2．3 性能优化方法
    1)流水线结构法 在滤波器中间增加适当的寄存器，构成流水线结构。在并行结构实现中添加流水线结构，可以提高滤波器速度，使其工作在更高的工作频率。对于速度固定的数据，可以通过多次复用乘累加器来节省资源。
    2)查找表分隔法 在用LUT实现分布式算法时，由于LUT的规模随着N的增加呈现指数增长，如果滤波器系数N过大，则查找表的规模十分庞大。为了减小规模，可以利用部分表计算。由于FIR滤波器是线性滤波器，因此低阶滤波器输出可以相加，由此定义一个高阶滤波器的输出。例如，把16输入的查找表分割成4个并行的查找表。
    查找表的分隔技术和流水线技术可以大大减小设计规模，同时并不会降低滤波速度。使用DA算法实现的FlR滤波器与传统的算法相比，DA算法可以极大地减少硬件电路规模，很容易实现流水线处理，提高电路的执行速度。

2．4 3种结构实现的比较
    改进串行结构、并行结构、DA结构实现的比较如下：
    1)改进串行结构 ①优点：使用资源少，只需一些寄存器、乘累加器便可完成整个滤波运算；②缺点：滤波速度慢，一次滤波所需的时钟数由滤波器的阶数决定。阶数较高的滤波器，滤波周期很大，无法实现高速滤波。
    2)并行结构 ①优点：完成滤波的速度快，直接并行滤波器可以在一个时钟周期内完成一次滤波；②缺点：消耗大量的乘累加器，器件延迟较大，工作频率不可能太高。
    3)DA结构 与串行结构实现相比，DA实现滤波速度较快，其滤波周期由数据宽度决定而与滤波器的阶数无关；而与并行实现相比，DA实现消耗的资源较少。且容易实现流水线处理，提高电路的执行速度。
    在设计中，当资源成本为主要制约时，根据速度要求，选择串行结构实现或DA结构实现；而当速度成为主要制约时，则根据资源成本因素，选择并行实现结构或DA结构实现。在一般的应用设计中，一般采用DA结构实现。

3 实例设计与仿真
3．1 FIR滤波器的设计
    利用Matlab中的FDATool工具设计一个33阶，Fs=48kHz，Fc=10．8 kHz的FIR滤波器，其幅值、相位响应见图3。为了便于FIR滤波器的FPGA实现，减小误差，将滤波器的系数量化取整后，在FPGA中实现采用的滤波系数为{-11，14，18，-11，-25，4，32，6，-38，-21，43，45，-47，-96，50，319，457，319，50，-96，-47，45，43，-21，-38，6，32，4，-25，-11，18，14，-11}。

3．2 FIR滤波器的FPGA实现与仿真
    在Xilinx 10．1 ISE平台中，选用Virtex-5系列的XC5VSXT50T器件，用Verilog HDL语言设计串行结构、并行结构的、以及DA结构，并在ModelSim中对3种结构实现进行仿真。设计中输入数据的位宽设为16位，而输入数据在运算处理前位宽扩展到17位。所用仿真激励为单位阶跃响应，时钟周期为Tck=10 ns。ModelSim中的仿真结果如图4所示。

图4中依次为改进的串行实现，并行实现和DA实现的仿真结果，其滤波周期分别为180 ns，10 ns和180 ns。上述设计的改进串行结构、并行结构和DA结构分别在XC5VSX50T中实现后，所消耗的FPGA内部各种资源如表1所示。

从表l可以看出，并行实现消耗的资源最多，其次是DA实现，最小是串行实现。而从滤波速度上来看，并行滤波速度最快，1个时钟周期便可滤波1次；而串行实现速度慢，其滤波周期取决于滤波器的阶数，对17阶的对称滤波器而言，滤波一次占9个时钟周期，滤波输出占1个时钟周期；相对串行实现和并行实现，DA实现的滤波周期取决于处理的数据宽度，上述设计中DA实现的滤波处理数据位宽是17位，所以滤波一次占17个时钟周期，滤波输出占用1个时钟周期。

4 结束语
    在实际应用中，当滤波器设计对滤波速度要求不高时，可采用串行结构或改进串行结构来实现，这样可以选取资源较少的器件，降低设计成本；当对滤波速度有较高要求时，可以考虑采用并行或DA来实现。并行实现滤波周期为时钟周期，速度快，但消耗的资源多，成本高；DA实现速度较快，消耗的资源较少，成本耗费较低。在数字多普勒接收机的实现过程中，根据接收机的性能要求以及所选用的FPGA器件资源，选取最优的FlR滤波器实现结构。随着FPGA查找技术的发展，具有较快的滤波速度和消耗较少资源的DA算法在FIR数字滤波领域得到了广泛应用。