趋肤效应

对于每个电气参数，必须考虑其数值有效时的频率范围。传输线的串联电阻也不例外。与其他参数一样，它也是频率的函数。图4.10画出了RG-58/U和等效串联电阻与频率的函数曲线。图中采用对数坐标轴。图4.10以相同的坐标轴绘出了感抗WL的曲线。

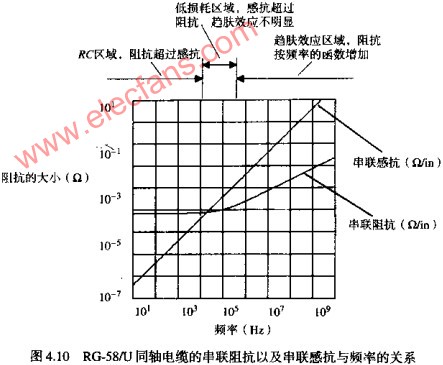
当频率低于W=R/L时，电阻超过感抗，电缆表现为一个RC传输线。当频率高于W=R/L时，电缆是一个低损耗传输线。

当频率高于0.1MHZ时，串联电阻开始增大。这导致更多的衰减，但相位保持线性。这种电阻的增加称为趋肤效应（SKIN EFFECT）。

传播因数的实部和虚部（（R+JWL）（JWC））1/2在图4.11中绘出，损耗单位为标培，相位单位为RAD（弧度）。1奈培等于8.69DB的损耗。图中显示了RC区域、固定衰减区域和趋肤效应区域。如图所示，相对于RC区域和趋肤效应区域，低损耗区域非常窄。

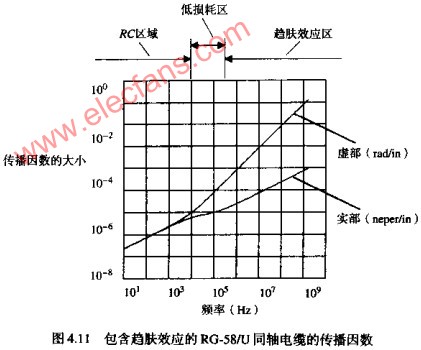
是什么导致了趋肤效应，它与导体外表层有什么关系呢？

1、趋肤效应的机理

在低频时，电流在导体内部的分布密度是均匀的。从导线的截面图看，中心和边缘区域电流的流量是相同的。

在高频时，导线表面的电流密度变大，而中心区域几乎没有电流流过。电流分布的变化如图4.12所示，低频时电流均匀地填满整个导线，高频时电流只从接近导线表面的地方流过。

为了形象地证明高频条件下电流的分布，首先假设导线纵向切成多层同心的长管，就像树桩上的年轮。

自然对称的形状可以阻止电流在环间流动，所以必须无误差地切割，所有电流绝对平行于导线的中心轴。

现在导线被切成许多环，我们可以分别考虑每个环的电感。靠近中心的环，像长而薄的管道，比外部的环有更大的电感。我们知道，在高频条件下，电流将从电感更低的通路流过。因此，高频条件下可以预计从外环通路流过的电流比内环更多。实际上正是如此。在高频条件下，绝大多数的电流聚集在靠近导体的外表面。

趋肤效应的作用力甚至比仅仅基于各个环管电感的预测作用更显著，实际上，环管间的互感也迫使电流紧贴着导线的外表面流过。

电流渗透的平均深度，称为趋肤深度。在高频条件下，趋肤深度是相当薄的。随着向内部的接近，在趋肤效应作用下，导体内部电流密度按指数规律下降，平均电流深度是频率W、导体的磁介系数U、电阻系数P的函数：

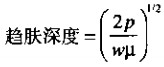
由于大多数电流在导体表面附近的一个薄的管道中流动，可以想象这个导体的视在电阻会大大增加。增加的大小是趋肤深度的函数。导体的视在电阻与电流流经的深度成反比。上式表明，趋肤深度与频率的平方根成反比。综合这些因素，导体的AC电阻与频率的平方根成正比增长。

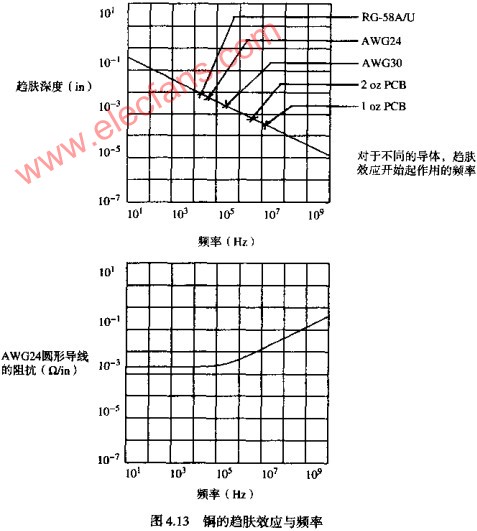
趋肤深度是材料的一个属性，随导体材料的整体导电率的不同而变化。它不是导体形状的函数。图4.13绘出了铜的趋肤深度与频率的函数曲线。图4.13中的第二条曲线给出了AWG24图形铜导线的电阻相对于频率的变化。当频率足够低时，趋肤深度等于或大于导线的半径，我们只考虑导线的总DC阻抗（电流分布在整个导体内）。当趋肤深度小于导线半径时，每个英寸的电阻与频率的平方根成正比增长。下式给出了趋肤深度在有限范围内的电阻。

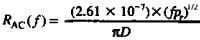
其中，D=线路直径，IN
      RAC=AC阻抗，Ω/IN
      PR=相对电阻系数（相对于铜）铜=1.00
      F=频率，HZ

在实践中，运用上式存在的问题是，低频时得出的电阻值为零。我们知道，直流时导线电阻是一个非零值。下式试图将AC和DC电阻模型合并到一个公式中。对于该复合模型，没有一个封闭型的解：下式仅仅是一个有用的近似。

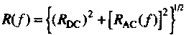
这一方程工更好地模拟了物理现实：低频时电阻保持常数，高频时电阻随频率的平方根成正比增长。电阻开始增长时的频率，等于趋肤深度开始小于导体厚度时的频率。对于圆形导体临界深度等于导体半径。对于扁平的矩形导体，例如印刷电路板走线，临界深度为导体厚度的一半。

对于方形导体，采用上两式时，用方形导体的周长替代πD，以英寸为单位。

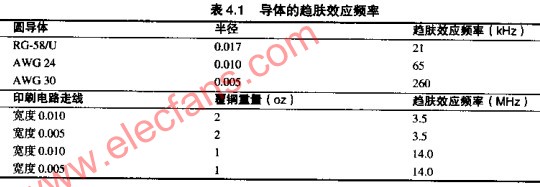
表4.1列出了各种导体中趋肤效应开始起作用的频率。

如果趋肤效应是一种表面化现象，那么增大表面面积应该对趋肤效应有所帮助。LITZ电缆正是这样做的。一段LITZ电缆多股导线构成，每股导线彼此之间都是绝缘的，以特定的绞合方式编织到一起。这一绞合保证了每股导线都受一同样大小的磁力作用，使得每股导线中流过的电流相等。多股导线使总表面积增大，降低了趋肤效应的电阻。LITZ电缆用于巨型超导电电磁线圈以及频率可达1MHZ的电机转子中。超过这个频率，使每股导线中的电流保持均衡就变得几乎不可能了。

2、趋肤效应区的频率响应

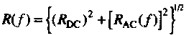用式（）替代式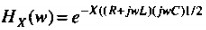（）中的R，可以预测出工作在趋肤效应区的传输线的衰减和相移。

以DB为单位的传输损耗与电阻成正比，式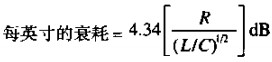（）。电阻与频率的平方根成正比。所以衰减的分贝数必然与频率的平方根成正比。这一结果清楚地显示在RG-174/U衰减曲线中，见图4.14。

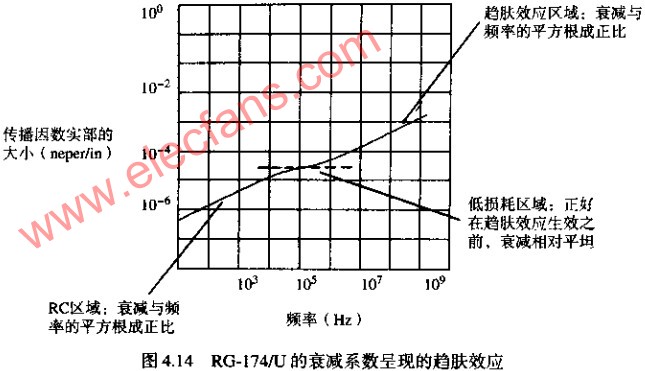
介绍传输线理论的文章常常重点关注图4.14的中心区域，位于RC区和趋肤效应区之间。在这个中心区域，电缆衰减随频率的变化是平坦的，不存在相位失真，而且特性阻抗也是平坦的，在这个区域，电缆看起来是理想状态。在实际情况中，即使这个理想的工作区域存在，也是在很窄的范围以内。

在趋肤效应区，电缆的长度减少一半会使它的频率响应有4倍的改善。这是因为衰减与电阻和长度之积成正比。当我们减少一半的长度，衰减也将减少一半。当我们把频率增加4倍时，衰减则增加两倍。

对于普通的数字传输线，总电阻限制在式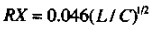（）的条件之内就仍然可以使用，但阻抗呈现出随频率而变化的特性。以数字转折频率点的趋肤效应电阻代入式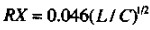（），会得到一个保守的精确结果。坚持这一准则，我们的传输电路总是会工作得很好，实际通过的上升沿将不会失真。

长距离的数字传输系统，采用的数据接收器比通常的TTL电路具有更大的电压容限，可以容忍大于0.2DB的损耗。损耗预算越大，可以使电路的工作距离越长。

采用式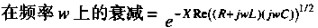（）直接算出数字转折频率处的预期损耗。在前式中加入趋肤效应电阻式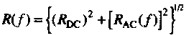（）作为R项。

在数字转折频率处限定损耗不超过0.5DB，可以使每个上升沿的95%的幅值都能通过。如果能够容忍一定程度的上升时间劣化，那么当计算0.5DB损耗的限定时，可以使用其转折频率值来算出到达接收器时所希望的信号上升时间。

长距离通信的另一个技巧是使数据编码具有相同数量的1和0，然后让它通过一个交流耦合网络。这个交流耦合的网络去除了数字信号中由驱动器产生的任何直流偏置分量。其结果是波形的高电平和低电平偏移相等。这个信号的接收器应该具有一个精确的过零决门限。这一方法能够容忍更大数量的衰减。

限制了连续1或0的最大数目的传输编码还能够容忍更大一些的衰减。图4.15举例说明了对于一个编码长度受限的系统，最坏情形下的码型。在A点，数据发送器开始传输一长串连续的1。在B点该长电缆的有限频率响应已经上升到一个最大值。在C点，这个小的数据脉冲通过，该数据脉冲的有效效率是FCLK/2，而整个数据码型的有效频率为FCLK/4N。如果这个电缆在FCLK/2处的频率响应幅值是在FCLK/4处幅值的一半，那么C点脉冲决不可能超过零点门限，而接收器也无法检测到它。

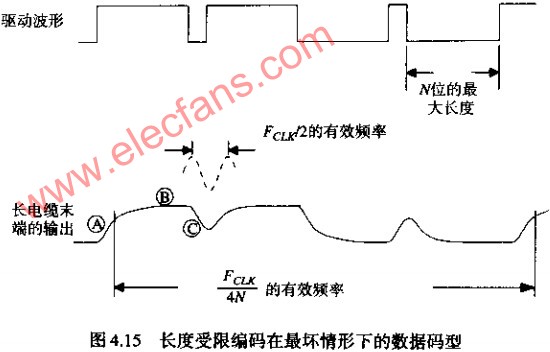
一个良好的习惯做法是，保证电缆足够短，以使一个编码长度受限系统相应的频率响应之比大于7：10：

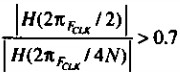
超出这个距离限制，就需要采用模拟信号的均衡方式。

3、趋肤效应区内的传输线阻抗

一旦越过临界频率R/L，WL项随W呈线性增长，而R（W）项因趋肤效应项也会与W1/2成正比增长。R（W）项相对于WL值一直很小，因此由式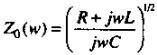（）给出的阻抗值仍然固定在（L/C）1/2。传输线的输入阻抗受趋肤效应的影响并不大。