

基于表面等离子激元的新型可调谐微共振环滤波器分析
调谐/滤波
26人已加入
描述
表面等离子激元(简称SPPs)早在1950年的Ritchie工作之后就被人们所认识。它们本质上是光子和导体中的自由电子相互作用而被表面俘获的广波,或者说是自由电子和光波电磁场由于共振频率相同而形成的一种集体振荡态。
SPPs沿着导体一电解质分界面处传播,传播距离大约是几百纳米到几微米,并在垂直表面的两个方向上,均以指数式衰减。传统光学由于衍射极限的限制,只能把光子器件做到波长(λ/n)量级,而无法满足集成光学的需求,而基于表面等离子激元的光子器件则打破了衍射极限的限制,可以将光束缚在亚波长结构中传播,故有利于光器件的集成化发展。
基于表面等离子激元的光波导由于可以将光场限制的很小,因而可以实现非常急剧的弯曲,进而可以做成非常小的环状波导。本文研究的基于表面等离子激元的共振环滤波器就是一种十分重要,也是十分基础的光学器件,在光通信中有着很广泛的应用(如光开关,波分复用等)。
1 表面等离子激元的特性
在合适的边界条件下解Maxwell方程,可以得到SPPs的色散关系:

其中,ε是金属的介电常数,εd是电介质的介电常数,kspp是SPPs的波矢,k0=ω/C是自由空间的波矢。色散关系公式(1)中,金属的介电常数ε采用Drude模型: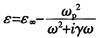 ,其中ε∞是带间跃迁对的介电常数,ω是等离子共振频率,γ是电子碰撞频率。由式(1)可以看出,由于kspp>k0,SPPs的动量与入射光子的动量不匹配,所以,在通常情况下,SPPs不能被激发,它可以通过在金属表面引入亚波长缺陷等方法来激发。
,其中ε∞是带间跃迁对的介电常数,ω是等离子共振频率,γ是电子碰撞频率。由式(1)可以看出,由于kspp>k0,SPPs的动量与入射光子的动量不匹配,所以,在通常情况下,SPPs不能被激发,它可以通过在金属表面引入亚波长缺陷等方法来激发。
2 可调谐谐振环滤波器结构分析
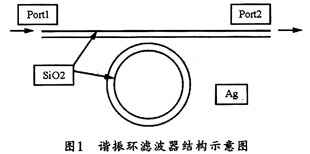
图1所示是基于表面等离子激元的结构模型,它由一根长直波导和一个环形波导构成,其波导材料均为sio2,周围覆盖的金属金、银、铝等都是常用的金属,对于在光频段来说,银(Ag)的损耗要小。该滤波器的具体数值:长直波导的宽度和环状波导宽度w均为200 nm。环的半径R是1μm,环与长直波导相距30 nm(直波导的下层到环形波导外层的距离)。光由入射端(端口1)进入长直波导,通过共振器(环形波导)在出射端(端口2)射出,出射强度由直波导中的导模和环状波导中的导模相互干射决定。由于环形波导中的导模位相是周期性变化的,因此估计出射端的光场强度也将随一定的周期变化。假设光在波导内的传播以及光的耦合没有损耗,而且在波导内只有单一模式传播,那么,理论上的透射率为:
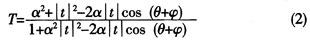
式中,θ是导模在环中每圈的相位增加,α代表导模在环中的损耗,包括传播损耗和环的弯曲损耗,t=∣t∣exp(j?)是复系数,表征的是没有被耦合进环形波导内的长直中的那部分导模。
3模拟仿真分析
仿真分析时,光源可采用平面波TM模,边界条件选取APML。图2所示是对该模型进行的仿真图。由图2可见,光在通过长直波导时,一部分光耦合进了环状波导。
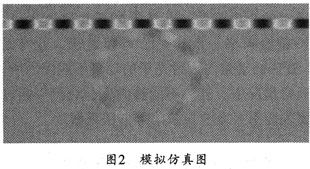
图3所示是R=1μm时,端口2(蓝色)和端口1(红色)出射归一化强度曲线,从图3可以看出,透射强确实随波长有周期性变化,在所示波长范围内出现了两个吸收峰(absorption peak),从透射公式(2)中可以得出,环的半径是影响透射结果的重要因素,为利于对比,接下来将半径改为1.1μm,并进行仿真,从而得到了图4所示的出射归一化强度曲线。
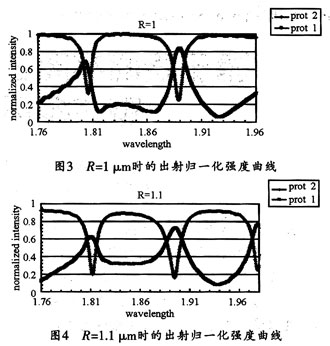
对比图3和图4可以看出,当R从1 μm变化到1.1 μm,吸收峰的位置整体向右偏移了,并且出现了3个吸收峰,R=1.1μm消光比(extinction ratio)要比R=1 μm时更大,吸收峰同样尖锐。图3中较好的1.8μm到1.9μm处的两个吸收峰的消光比大约是8db,-3db带宽大约是8nm,好于现有水准。另一个重要的衡量滤波器的系数是FSR(passband bandwidth and extinction ratio),在本文中,可以简单地理解为相邻吸收峰的距离,R=1μm时是90 nm,同样波长范围内,R=1.1时则出现了3个吸收峰,说明当R变大时,FSR反而变小,经测量大约是86 nm。可以推断,当环继续增大,吸收峰间距也许能满足DWDM的需要,从而为DWDM大型集成化提供可能。
4 结束语
本文分析了基于表面等离子激元的可调谐共振环滤波器结构原理,并分别对环半径R为1.0μm和1.1 μm时进行了仿真。结果发现,波导环半径的变化会周期性地在特定波长上产生强烈的吸收效果,其中-3 db带宽只有8 nm,好于现有水准,且随着环半径R的增大,吸收峰会向右移动,而且可以通过改变金属温度的方法对滤波器进行调谐。通过计算在所示波长范围内,所有峰的数量可知,随着环状波导半径R的增大,吸收峰会更密集(FSR减小),而当环的半径继续增大,吸收峰间距越来越小,但峰依然尖锐,可以符合密集波分复用(DWDM)的需求,应用前景光明。另外,本研究模型结构简单,整个模型大小不超过10μm2,而且比现有的光子晶体器件小,很易于集成。
打开APP阅读更多精彩内容
SPPs沿着导体一电解质分界面处传播,传播距离大约是几百纳米到几微米,并在垂直表面的两个方向上,均以指数式衰减。传统光学由于衍射极限的限制,只能把光子器件做到波长(λ/n)量级,而无法满足集成光学的需求,而基于表面等离子激元的光子器件则打破了衍射极限的限制,可以将光束缚在亚波长结构中传播,故有利于光器件的集成化发展。
基于表面等离子激元的光波导由于可以将光场限制的很小,因而可以实现非常急剧的弯曲,进而可以做成非常小的环状波导。本文研究的基于表面等离子激元的共振环滤波器就是一种十分重要,也是十分基础的光学器件,在光通信中有着很广泛的应用(如光开关,波分复用等)。
1 表面等离子激元的特性
在合适的边界条件下解Maxwell方程,可以得到SPPs的色散关系:

其中,ε是金属的介电常数,εd是电介质的介电常数,kspp是SPPs的波矢,k0=ω/C是自由空间的波矢。色散关系公式(1)中,金属的介电常数ε采用Drude模型:
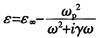 ,其中ε∞是带间跃迁对的介电常数,ω是等离子共振频率,γ是电子碰撞频率。由式(1)可以看出,由于kspp>k0,SPPs的动量与入射光子的动量不匹配,所以,在通常情况下,SPPs不能被激发,它可以通过在金属表面引入亚波长缺陷等方法来激发。
,其中ε∞是带间跃迁对的介电常数,ω是等离子共振频率,γ是电子碰撞频率。由式(1)可以看出,由于kspp>k0,SPPs的动量与入射光子的动量不匹配,所以,在通常情况下,SPPs不能被激发,它可以通过在金属表面引入亚波长缺陷等方法来激发。2 可调谐谐振环滤波器结构分析
图1所示是基于表面等离子激元的结构模型,它由一根长直波导和一个环形波导构成,其波导材料均为sio2,周围覆盖的金属金、银、铝等都是常用的金属,对于在光频段来说,银(Ag)的损耗要小。该滤波器的具体数值:长直波导的宽度和环状波导宽度w均为200 nm。环的半径R是1μm,环与长直波导相距30 nm(直波导的下层到环形波导外层的距离)。光由入射端(端口1)进入长直波导,通过共振器(环形波导)在出射端(端口2)射出,出射强度由直波导中的导模和环状波导中的导模相互干射决定。由于环形波导中的导模位相是周期性变化的,因此估计出射端的光场强度也将随一定的周期变化。假设光在波导内的传播以及光的耦合没有损耗,而且在波导内只有单一模式传播,那么,理论上的透射率为:
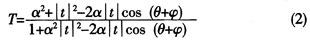

式中,θ是导模在环中每圈的相位增加,α代表导模在环中的损耗,包括传播损耗和环的弯曲损耗,t=∣t∣exp(j?)是复系数,表征的是没有被耦合进环形波导内的长直中的那部分导模。
3模拟仿真分析
仿真分析时,光源可采用平面波TM模,边界条件选取APML。图2所示是对该模型进行的仿真图。由图2可见,光在通过长直波导时,一部分光耦合进了环状波导。

图3所示是R=1μm时,端口2(蓝色)和端口1(红色)出射归一化强度曲线,从图3可以看出,透射强确实随波长有周期性变化,在所示波长范围内出现了两个吸收峰(absorption peak),从透射公式(2)中可以得出,环的半径是影响透射结果的重要因素,为利于对比,接下来将半径改为1.1μm,并进行仿真,从而得到了图4所示的出射归一化强度曲线。

对比图3和图4可以看出,当R从1 μm变化到1.1 μm,吸收峰的位置整体向右偏移了,并且出现了3个吸收峰,R=1.1μm消光比(extinction ratio)要比R=1 μm时更大,吸收峰同样尖锐。图3中较好的1.8μm到1.9μm处的两个吸收峰的消光比大约是8db,-3db带宽大约是8nm,好于现有水准。另一个重要的衡量滤波器的系数是FSR(passband bandwidth and extinction ratio),在本文中,可以简单地理解为相邻吸收峰的距离,R=1μm时是90 nm,同样波长范围内,R=1.1时则出现了3个吸收峰,说明当R变大时,FSR反而变小,经测量大约是86 nm。可以推断,当环继续增大,吸收峰间距也许能满足DWDM的需要,从而为DWDM大型集成化提供可能。
4 结束语
本文分析了基于表面等离子激元的可调谐共振环滤波器结构原理,并分别对环半径R为1.0μm和1.1 μm时进行了仿真。结果发现,波导环半径的变化会周期性地在特定波长上产生强烈的吸收效果,其中-3 db带宽只有8 nm,好于现有水准,且随着环半径R的增大,吸收峰会向右移动,而且可以通过改变金属温度的方法对滤波器进行调谐。通过计算在所示波长范围内,所有峰的数量可知,随着环状波导半径R的增大,吸收峰会更密集(FSR减小),而当环的半径继续增大,吸收峰间距越来越小,但峰依然尖锐,可以符合密集波分复用(DWDM)的需求,应用前景光明。另外,本研究模型结构简单,整个模型大小不超过10μm2,而且比现有的光子晶体器件小,很易于集成。
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
OptiFDTD应用:纳米盘型谐振腔等离子体波导滤波器2025-01-09 742
-
采用光纤环实现可调谐微波光子滤波器2019-07-26 2015
-
基于表面等离子激元的共振环滤波器,不看肯定后悔2021-04-14 1028
-
光纤表面等离子体共振传感检测系统共振波长的红移2010-08-25 634
-
表面等离子共振型免疫传感器2009-03-06 1227
-
可调谐陷波滤波器2009-09-16 1086
-
表面等离子激元的新型可调谐微共振环滤波器技术2010-06-11 1230
-
表面等离子共振技术在生物医学中的应用2011-02-11 818
-
表面等离子共振的原理及在生物医学中的应用2011-02-17 1020
-
Ag_TiO_2薄膜表面等离子体共振光谱特性研究_刘超2017-03-19 703
-
基于光纤可调谐滤波器的背景介绍2017-09-21 926
-
表面等离子体激元增强非晶态硅氮化合物的发光效率详解2017-10-27 1047
-
数字可调谐微带滤波器2018-02-08 1035
-
光纤可调谐滤波器怎么选?光纤可调谐滤波器的类型2023-07-14 4838
-
Analog Devices Inc. ADMV8526数字可调谐滤波器数据手册2025-06-22 636
全部0条评论

快来发表一下你的评论吧 !

