

遗传算法对PFC控制电路的优化设计分析
电源设计应用
描述
1 PFC控制电路电流环补偿网络设计
PFC技术适应了电力电子技术的发展方向,其控制原理都是,在一定规律的导通比控制下,完成从直流电压到直流电压的变换,控制输入电流波形跟踪输入电压波形,以达到功率因数校正的目的。PFC控制电路采用平均电流控制方法。平均电流控制电路结构如图1所示。
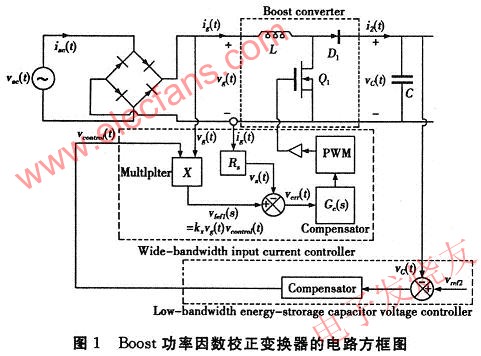
对Boost变换器而言,在滤波器的共振频段(LCO)与开关切换频段间的范围内,电流环开环为一阶积分系统,电流环控制信号对输入电流的转移函数为:
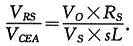
其中,VRS为输入电流检测电阻RS两端的跨压,VCEA为电流误差放大器的输出电压,VO为直流输出电压,VS为震荡器三角波的峰峰值的大小,sL为Boost变换器的电感阻抗。
为保证系统稳定地运行,必须对电流环进行补偿。电流调节器的零点必须处于或小于最大截止频率fCI,此时系统刚好有45°的相角裕量。为了消除系统在开关频率处对噪声的敏感,应在电流调节器中引入一个极点,极点频率为1/2开关频率,当极点频率大于1/2开关频率时,极点就不会对电流环路的频率响应产生影响。
电流环补偿网络如图2所示:
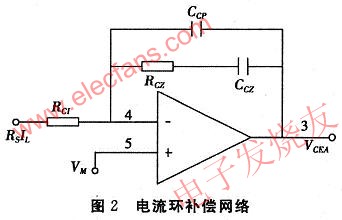
其传递函数:

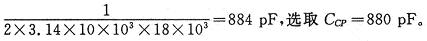
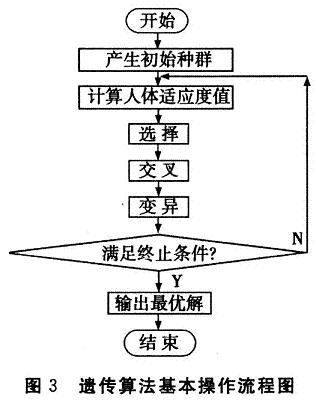
2 遗传算法的改进设计
在应用遗传算法优化的控制器参数时,本文在标准遗传算法的基础上,做出了如下设计:
(1)在编码方案上,采用格雷编码来克服二进制编码的“Hamming悬崖”;
(2)选择操作中,用期望值法来代替适应度值比例法,以避免个体数目不太大时,适应度值比例法依据随机数来选择个体有时不能正确反映个体的适应度;
(3)交叉操作考虑使用两点交叉,使优良的基因模式尽可能地组合在一起。
在此基础之上,对算法进行了以下改进:
①保护优秀个体。
在每一代种群中适应度值最大的个体保留下来,不参加交叉和变异过程,使之直接进入下一代,这样可以防止优秀的个体在交叉或变异操作中被破坏从而保证了全局收敛。
②自适应变异策略。
对交叉和变异算子采用基于自适应温度的自适应策略。将这种自适应策略同时应用于交叉和变异操作,并定义为自适应温度:
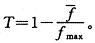
其中,f,fmax分别为某一代的平均和最优个体适应度值。易知,随着迭代的进行,“温度”是逐渐下降的。然后以T为依据设计遗传算子:
PC=a+bT,PM=c-dT.
a,b,c,d为恰当选择的常数,这时算子和自适应温度T呈简单的线性关系。
③综合条件终止进化。
综合两个条件来判断算法是否终止进化的条件——一是,遗传代数是否达到固定的最大遗传代数;二是,计算前后几代个体平均适应度的差或方差是否小于设定的极小阈值时。两个条件相与,即两个条件满足一个时,就认为符合终止进化条件。
3 遗传算法控制参数优化设计
为了使PFC电路有较好的稳定性和动态性能,必须对电流环和电压环进行反馈综合,通过适当的补偿网络,合理配置零极点,改善电路特性。
电流环反馈补偿网络采用如图2所示的单零点双极点网络。
则电流环的开环传递函数为:
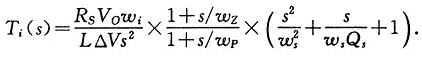
其中:RS为电流采样电阻,VO为输出电压,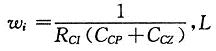 为主电路电感,△V为PWM控制器三角波峰峰值,
为主电路电感,△V为PWM控制器三角波峰峰值,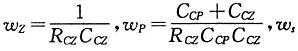 为切换频率
为切换频率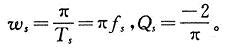 选择设计变量为X=[x1,x2,x3,x4]=[RCI,CCP,RCZ,CCZ],则可求出电流环的开环传递函数与设计变量之间的关系式:
选择设计变量为X=[x1,x2,x3,x4]=[RCI,CCP,RCZ,CCZ],则可求出电流环的开环传递函数与设计变量之间的关系式:
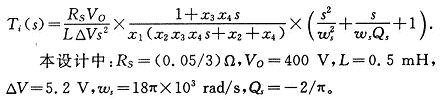
采用C语言编写程序,并用SIMULINK进行仿真。
待优化控制参数为X=[x1,x2,x3,x4]=[RCI,CCP,RCZ,CCZ],属于多参数优化问题。将各参数分别用10位格雷码表示,并将其首尾串联,形成40位的染色体串。初始种群X=[x1,x2,x3,x4]=[RCI,CCP,RCZ,CCZ]初始值以上一节初步设计各参量的取值X*为中心,在一定范围内向两边取值即X0=X*×(1士δ),取δ=0.3。
种群规模:N=31;最大迭代次数:Gmax=400;每次遗传操作后保留一个最优个体;
遗传算子系数取为:
a=0.6,b=0.2,c=0.2,d=0.19,即:PC=a+bT=0.6+0.2T,PM=c-dT=0.2-0.19T。
采用大变异策略PC,PM的变化范围为0.6~0.8和0.01~0.2。
将系统在单位阶跃函数下的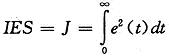 、电流环传递函数TI(s)的开环穿越频率WCI结合,分别取一定权值作为评价函数,但因为遗传算法只针对最大值且不能为负,所以适应度函数取为其倒数:
、电流环传递函数TI(s)的开环穿越频率WCI结合,分别取一定权值作为评价函数,但因为遗传算法只针对最大值且不能为负,所以适应度函数取为其倒数:
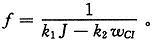
其中,k1、k2分别为两个评价因子的权,优化过程中取为0.5。
因为采用连续参数编码,而实际工程中元件参数是标准化参数,在优化过程中,采用动态规划思想进行分部设计。即:
首先,对四个参数进行编码并优化,将得出的最优值与标准参数对比,选取最接近标准参数或由最多两个标准元件串联(或并联)能够得到的一个参数值,将其确定。然后,对剩下的三个参数重新编码、寻优、确定第二个参数。以此类推,直至四个参数全部确定。
4 实验结果分析
我们应用本文提出的改进的遗传算法(Modified Genet-ic Algorithms简称MGA)进行了参数优化,其结果和频域初步设计结果对比及两组参数下电流环暂态响应性能指标分别如表1、表2所示:
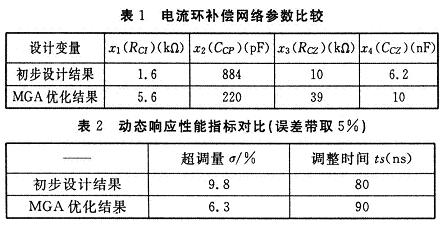
分别应用两组参数阶越响应进行仿真,仿真结果比较如图4:
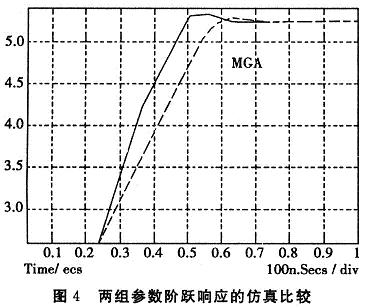
由图4可以明显地看出超调量减小,过渡时间缩短,控制系统的时域性能指标有很大改善。仿真结果说明了优化参数的有效性与优越性。
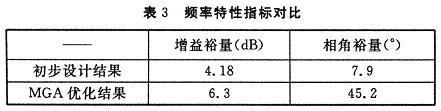
结合频域分析,电流环优化前后的频率特性指标如表3所示。
优化设计前后电流环开环传递函数的频率特性如图5所示。
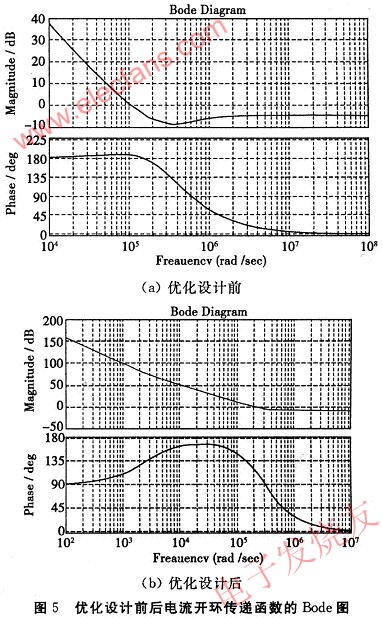
由以上的优化设计结果可见,与初步设计值相比,经过优化后,电流环的增益裕量和相位裕量都增大了,电流环的稳定性能得到了改善,开关噪声抑制能力也优于优化前。
5 结束语
本文在分析研究遗传算法基本原理与操作方法的基础上,对遗传算法操作方法进行了改进,并对平均电流控制功率因数控制电路,进行了电路分析和控制参数的初步设计,利用改进的遗传算法对控制参数进行了优化.并对优化结果进行了仿真分析。
以后工作中有待进一步深入研究的问题有:应用遗传算法对控制参数离线进行优化选择,采用模拟器件实现控制,今后能否进一步优化算法,使算法实现占用内存空间足够小、运行时间足够短,以实现数字在线优化控制。
-
基于改进遗传算法的图像分割方法2009-09-19 3368
-
基于遗传算法的片上网络虚通道分配算法2010-04-22 2620
-
遗传算法辨识程序2018-01-04 1929
-
基于遗传算法的异步电机2019-12-10 2833
-
基于遗传算法优化EKF算法的SOC估算2020-03-12 7791
-
遗传算法的优化 精选资料分享2021-07-12 1889
-
什么是遗传算法?2021-11-22 1914
-
遗传算法的特点和应用概述2021-12-31 1666
-
遗传算法在管网优化设计中的应用2009-01-09 626
-
基于遗传算法的PID 控制及其MATLAB 仿真2009-06-11 1014
-
基于遗传算法的非确定性目标优化2010-01-12 573
-
基于遗传算法的直流转台控制参数优化2010-02-11 900
-
Optimization_优化遗传算法2016-07-20 782
-
遗传算法在函数优化中研究(MATLAB测试)2017-11-10 1023
-
遗传算法的解析与基于遗传算法的机器学习的介绍2017-11-13 865
全部0条评论

快来发表一下你的评论吧 !

