

视频压缩的基本原理
电子常识
描述
视频压缩的基本原理
6.1.1 视频信号压缩的可能性
视频数据中存在着大量的冗余, 即图像的各像素数据之间存在极强的相关性。 利用这些相关性, 一部分像素的数据可以由另一部分像素的数据推导出来, 结果视频数据量能极大地压缩, 有利于传输和存储。 视频数据主要存在以下形式的冗余。
1. 空间冗余
视频图像在水平方向相邻像素之间、 垂直方向相邻像素之间的变化一般都很小, 存在着极强的空间相关性。 特别是同一景物各点的灰度和颜色之间往往存在着空间连贯性, 从而产生了空间冗余, 常称为帧内相关性。
2. 时间冗余
在相邻场或相邻帧的对应像素之间, 亮度和色度信息存在着极强的相关性。 当前帧图像往往具有与前、 后两帧图像相同的背景和移动物体, 只不过移动物体所在的空间位置略有不同, 对大多数像素来说, 亮度和色度信息是基本相同的, 称为帧间相关性或时间相关性。
3. 结构冗余
在有些图像的纹理区, 图像的像素值存在着明显的分布模式。 如方格状的地板图案等。 已知分布模式, 可以通过某一过程生成图像, 称为结构冗余。
4. 知识冗余
有些图像与某些知识有相当大的相关性。 如人脸的图像有固定的结构, 嘴的上方有鼻子, 鼻子的上方有眼睛, 鼻子位于脸部图像的中线上。 这类规律性的结构可由先验知识得到, 此类冗余称为知识冗余。
5. 视觉冗余
人眼具有视觉非均匀特性, 对视觉不敏感的信息可以适当地舍弃。 在记录原始的图像数据时, 通常假定视觉系统是线性的和均匀的, 对视觉敏感和不敏感的部分同等对待, 从而产生了比理想编码(即把视觉敏感和不敏感的部分区分开来编码)更多的数据, 这就是视觉冗余。 人眼对图像细节、 幅度变化和图像的运动并非同时具有最高的分辨能力。
人眼视觉对图像的空间分解力和时间分解力的要求具有交换性, 当对一方要求较高时, 对另一方的要求就较低。 根据这个特点, 可以采用运动检测自适应技术, 对静止图像或慢运动图像降低其时间轴抽样频率, 例如每两帧传送一帧; 对快速运动图像降低其空间抽样频率。
另外, 人眼视觉对图像的空间、 时间分解力的要求与对幅度分解力的要求也具有交换性, 对图像的幅度误差存在一个随图像内容而变的可觉察门限, 低于门限的幅度误差不被察觉, 在图像的空间边缘(轮廓)或时间边缘(景物突变瞬间)附近, 可觉察门限比远离边缘处增大3~4倍, 这就是视觉掩盖效应。
根据这个特点, 可以采用边缘检测自适应技术, 对于图像的平缓区或正交变换后代表图像低频成分的系数细量化, 对图像轮廓附近或正交变换后代表图像高频成分的系数粗量化; 当由于景物的快速运动而使帧间预测编码码率高于正常值时进行粗量化, 反之则进行细量化。 在量化中, 尽量使每种情况下所产生的幅度误差刚好处于可觉察门限之下, 这样能实现较高的数据压缩率而主观评价不变。
6. 图像区域的相同性冗余
在图像中的两个或多个区域所对应的所有像素值相同或相近, 从而产生的数据重复性存储, 这就是图像区域的相似性冗余。 在这种情况下, 记录了一个区域中各像素的颜色值, 与其相同或相近的区域就不再记录各像素的值。 矢量量化方法就是针对这种冗余图像的压缩方法。
7. 纹理的统计冗余
有些图像纹理尽管不严格服从某一分布规律, 但是在统计的意义上服从该规律, 利用这种性质也可以减少表示图像的数据量, 称为纹理的统计冗余。
电视图像信号数据存在的信息冗余为视频压缩编码提供了可能。
6.1.2 视频信号的数字化和压缩
模拟电视信号(包括视频和音频)通过取样、 量化后编码 为二进制数字信号的过程称为模数变换(A/D变换)或脉冲编码调制(PCM, Pulse Coding Modulation), 所得到的信号也称为PCM信号, 其过程可用图6-1(a)表示。 若取样频率等于fs、 用n比特量化, 则PCM信号的码率为nfs(比特/s)。 PCM编码既可以对彩色全电视信号直接进行, 也可以对亮度信号和两个色差信号分别进行, 前者称为全信号编码, 后者称为分量编码。
PCM信号经解码和插入滤波恢复为模拟信号, 如图6-1(b)所示, 解码是编码的逆过程, 插入滤波是把解码后的信号插补为平滑、 连续的模拟信号。 这两个步骤合称为数模变换(D/A变换)或PCM解码。

图 6-1 电视信号的数字化和复原
(a) A/D变换; (b) D/A变换
1. 奈奎斯特取样定理
理想取样时, 只要取样频率大于或等于模拟信号中最高频率的两倍, 就可以不失真地恢复模拟信号, 称为奈奎斯特取样定理。 模拟信号中最高频率的两倍称为折叠频率。
2. 亚奈奎斯特取样
按取样定理, 若取样频率fs小于模拟信号最高频率fmax的2倍会产生混叠失真, 但若巧妙地选择取样频率, 令取样后频谱中的混叠分量落在色度分量和亮度分量之间, 就可用梳状滤波器去掉混叠成分。
3. 均匀量化和非均匀量化
在输入信号的动态范围内, 量化间隔幅度都相等的量化称为均匀量化或线性量化。 对于量化间距固定的均匀量化, 信噪比随输入信号幅度的增加而增加, 在强信号时固然可把噪波淹没掉, 在弱信号时, 噪波的干扰就十分显著。
为改善弱信号时的信噪比, 量化间距应随输入信号幅度而变化, 大信号时进行粗量化, 小信号时进行细量化, 也就是采用非均匀量化(或称非线性量化)。
非均匀量化有两种方法, 一是把非线性处理放在编码器前和解码器后的模拟部分, 编、 解码仍采用均匀量化, 在均匀量化编码器之前, 对输入信号进行压缩, 这样等效于对大信号进行粗量化, 小信号进行细量化; 在均匀量化解码器之后, 再进行扩张, 以恢复原信号。 另一种方法是直接采用非均匀量化器, 输入信号大时进行粗量化(量化间距大) , 输入信号小时细量化(量化间距小)。 也有采用若干个量化间距不等的均匀量化器, 当输入信号超过某一电平时进入粗间距均匀量化器, 低于某一电平时进入细间距量化器, 称为准瞬时压扩方式。
通常用Q表示量化, 用Q-1表示反量化。 量化过程相当于由输入值找到它所在的区间号, 反量化过程相当于由量化区间号得到对应的量化电平值。 量化区间总数远远少于输入值的总数, 所以量化能实现数据压缩。 很明显, 反量化后并不能保证得到原来的值, 因此量化过程是一个不可逆过程, 用量化的方法来进行压缩编码是一种非信息保持型编码。 通常这两个过程均可用查表方法实现, 量化过程在编码端完成, 而反量化过程则在解码端完成。
对量化区间标号(量化值)的编码一般采用等长编码方法。 当量化分层总数为K时, 经过量化压缩后的二进制数码率为lbK比特/量值。 在一些要求较高的场合, 可采用可变字长编码如哈夫曼编码或算术编码来进一步提高编码效率。
6.1.3 ITU-R BT.601分量数字系统
数字视频信号是将模拟视频信号经过取样、 量化和编码后形成的。 模拟电视有PAL、 NTSC等制式, 必然会形成不同制式的数字视频信号, 不便于国际数字视频信号的互通。 1982年10月, 国际无线电咨询委员会(CCIR, Consultative Committee for International Radio)通过了第一个关于演播室彩色电视信号数字编码的建议, 1993年变更为ITU-R(国际电联无线电通信部分, International Telecommunications Union-Radio communications Sector)BT.601分量数字系统建议。
BT.601建议采用了对亮度信号和两个色差信号分别编码的分量编码方式, 对不同制式的信号采用相同的取样频率13.5 MHz, 与任何制式的彩色副载波频率无关, 对亮度信号Y的取样频率为13.5 MHz。 由于色度信号的带宽远比亮度信号的带宽窄, 对色度信号U和V的取样频率为6.75 MHz。 每个数字有效行分别有720个亮度取样点和360×2个色差信号取样点。 对每个分量的取样点都是均匀量化, 对每个取样进行8比特精度的PCM编码。
这几个参数对525行、 60场/秒和625行50场/秒的制式都是相同的。 有效取样点是指只有行、 场扫描正程的样点有效, 逆程的样点不在PCM编码的范围内。 因为在数字化的视频信号中, 不再需要行、 场同步信号和消隐信号, 只要有行、 场(帧)的起始位置即可。 例如, 对于PAL制, 传输所有的样点数据, 大约需要200 Mb/s的传输速率, 传输有效样点只需要160 Mb/s左右的速率。
色度信号的取样率是亮度信号取样率的一半, 常称作4∶2∶2格式, 可以理解为每一行里的Y、 U、 V的样点数之比为4∶2∶2。
6.1.4 熵编码
熵编码(Entropy Coding)是一类无损编码, 因编码后的平均码长接近信源的熵而得名。 熵编码多用可变字长编码(VLC, Variable Length Coding)实现。 其基本原理是对信源中出现概率大的符号赋以短码, 对出现概率小的符号赋以长码, 从而在统计上获得较短的平均码长。 所编的码应是即时可译码, 某一个码不会是另一个码的前缀, 各个码之间无需附加信息便可自然分开。
1. 霍夫曼(Huffman)编码
霍夫曼(Huffman)编码是一种可变长编码, 编码方法如图6-2所示。
(1) 将输入信号符号以出现概率由大至小为序排成一列。
(2) 将两处最小概率的符号相加合成为一个新概率, 再按出现概率的大小排序。
(3) 重复步骤(2), 直至最终只剩两个概率。
(4) 编码从最后一步出发逐步向前进行, 概率大的符号赋予“0”码, 另一个概率赋予“1”码, 直至到达最初的概率排列为止。 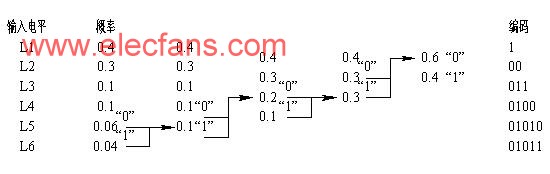
图 6-2 霍夫曼(Huffman)编码
2. 算术编码
霍夫曼编码的每个代码都要使用一个整数位, 如果一个符号只需要用2.5位就能表示, 但在霍夫曼编码中却必须用3个符号来表示, 因此它的效率较低。 与其相比, 算术编码并不是为每个符号产生一个单独的代码, 而是使整条信息共用一个代码, 增加到信息上的每个新符号都递增地修改输出代码。
假设信源由4个符号S1、 S2、 S3和S4组成, 其概率模型如表6-1所示。 把各符号出现的概率表示在如图6-3所示的单位概率区间之中, 区间的宽度代表概率值的大小, 各符号所对应的子区间的边界值, 实际上是从左到右各符号的累积概率。 在算术编码中通常采用二进制的小数来表示概率, 每个符号所对应的概率区间都是半开区间, 如S1对应[0, 0.001), S2对应[0.001, 0.011)。 算术编码所产生的码字实际上是一个二进制小数值的指针, 该指针指向所编的符号所对应的概率区间。
表6-1 信源概率模型和算术编码过程 

图 6-3 算术编码过程示意图
若将符号序列S3S3S2S4进行算术编码, 序列的第一个符号为S3, 我们用指向图6-3中第3个子区间的指针来代表这个符号, 由此得到码字0.011。 后续的编码将在前面编码指向的子区间内进行。 将[0.011, 0.111)区间再按符号的概率值划分成4份, 对第二个符号S3, 指针指向0.1001,码 字串变为0.1001。 然后S3所对应的子区间又被划分为4份, 开始对第3个符号进行编码……。
算术编码的基本法则如下:
(1) 初始状态: 编码点(指针所指处)C0=0, 区间宽度A0=1。
(2) 新编码点: Ci= Ci-1 + Ai-1×Pi。
式中, Ci-1是原编码点; Ai-1是原区间宽度;
Pi所编符号对应的累积概率。
新区间宽度Ai= Ai-1×pi
式中, pi为所编符号对应的概率。
根据上述法则, 对序列S3S3S2S4进行算术编码的过程如下:
第一个符号S3:
C1=C0+A0×P1=0+1×0.011=0.011
A1=A0×p1=1×0.1=0.1
[0.011,0.111]
第二个符号S3: C2=C1+A1×P2
=0.011+0.1×0.011=0.1001
A2=A1×p2=0.1×0.1=0.01
[0.1001,0.1101]
第三个符号S2:
C3=C2+A2×P3=0.1001+0.01×0.001=0.10011
A3=A2×p3=0.01×0.01=0.0001
[0.10011,0.10101]
第四个符号S4: C4=C3+A3×P4=0.10011+0.0001×0.111=0.1010011
A4=A3×p4=0.0001×0.001=0.0000001
[0.1010011,0.10101)
3. 游程编码
游程编码(RLC, Run Length Coding)是一种十分简单的压缩方法, 它将数据流中连续出现的字符用单一的记号来表示。 例如, 字符串5310000000000110000000012000000000000可以压缩为5310-10110-08120-12, 其中, “-”后面两个数字是“-”前面数字的连续个数。 游程编码的压缩率不高, 但编码、 解码的速度快, 仍被得到广泛的应用, 特别是在变换编码后再进行游程编码, 有很好的效果。
6.1.5 预测编码和变换编码
1. DPCM原理
基于图像的统计特性进行数据压缩的基本方法就是预测编码。 它是利用图像信号的空间或时间相关性, 用已传输的像素对当前的像素进行预测, 然后对预测值与真实值的差——预测误差进行编码处理和传输。 目前用得较多的是线性预测方法, 全称为差值脉冲编码调制(DPCM, Differential Pulse Code Modulation), 简称为DPCM。
利用帧内相关性(像素间、 行间的相关)的DPCM称为帧内预测编码。 如果对亮度信号和两个色差信号分别进行DPCM编码, 对亮度信号采用较高的取样率和较多位数编码, 对色差信号用较低的取样率和较少位数编码, 构成时分复合信号后再进行DPCM编码, 这样做使总码率更低。
利用帧间相关性(邻近帧的时间相关性)的DPCM被称为帧间预测编码, 因帧间相关性大于帧内相关性, 其编码效率更高。 若把这两种DPCM组合起来, 再配上变字长编码技术, 能取得较好的压缩效果。 DPCM是图像编码技术中研究得最早, 且应用最广的一种方法, 它的一个重要的特点是算法简单, 易于硬件实现。 图6-4(a)是它的示意图, 编码单元主要包括线性预测器和量化器两部分。
编码器的输出不是图像像素的样值f(m, n), 而是该样值与预测值g(m, n)之间的差值, 即预测误差e(m, n)的量化值E(m, n)。 根据图像信号统计特性的分析, 给出一组恰当的预测系数, 使预测误差主要分布在“0”附近, 经非均匀量化, 采用较少的量化分层, 图像数据得到压缩。 而量化噪声又不易被人眼所觉察, 图像的主观质量并不明显下降。 图6-4(b)是DPCM解码器, 其原理和编码器刚好相反。 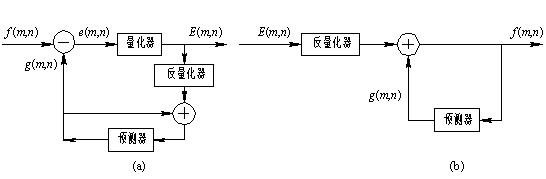
图 6-4 DPCM原理
(a) DPCM编码器; (b) DPCM解码器
DPCM编码性能主要取决于预测器的设计, 预测器设计要确定预测器的阶数N以及各预测系数。 图6-5是一个4阶预测器的示意图, 图6-5(a)表示预测器所用的输入像素和被预测像素之间的位置关系, 图6-5(b)表示预测器的结构。
更详细请查看:http://www.elecfans.com/soft/courseware/2010/2010093090940.html
- 相关推荐
- 视频压缩
-
H264视频压缩编码标准2012-08-20 0
-
基于SOC架构的高清视频压缩技术2020-02-20 0
-
怎么在FPGA设计中使用先进的视频压缩技术?2021-04-08 0
-
鸿蒙怎么实现视频压缩?2021-05-28 0
-
视频增强算法的基本原理是什么?2021-06-03 0
-
视频压缩算法的特点和处理流程是怎样的?2021-06-08 0
-
什么是视频压缩?2021-06-08 0
-
avi/rm/rmvb/wmv视频压缩工具下载2009-04-24 1172
-
视频压缩IPcore设计2009-11-30 584
-
视频压缩技术2010-09-30 1701
-
基于ADV212的高清视频压缩系统设计策略2010-04-23 2469
-
基于Android系统的H.264视频压缩技术实现2015-11-18 589
-
视频压缩简介(一)2019-03-02 651
-
视频压缩越发常见,但压缩真的是越小越好吗?2020-08-07 6225
-
视频压缩是什么?视频压缩有什么好处?2020-08-07 33448
全部0条评论

快来发表一下你的评论吧 !

