阻抗匹配的理想模型

什么是阻抗

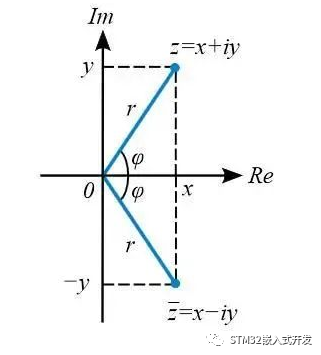
在电学中，常把对电路中电流所起的阻碍作用叫做阻抗。阻抗单位为欧姆，常用Z表示，是一个复数：

Z= R+i( ωL–1/(ωC))

具体说来阻抗可分为两个部分，电阻（实部）和电抗（虚部）。

其中电抗又包括容抗和感抗，由电容引起的电流阻碍称为容抗，由电感引起的电流阻碍称为感抗。

阻抗匹配的理想模型

射频工程师大都遇到过匹配阻抗的问题，通俗的讲，阻抗匹配的目的是确保能实现信号或能量从“信号源”到“负载”的有效传送。

其最最理想模型当然是希望Source端的输出阻抗为50欧姆，传输线的阻抗为50欧姆，Load端的输入阻抗也是50欧姆，一路50欧姆下去，这是最理想的。

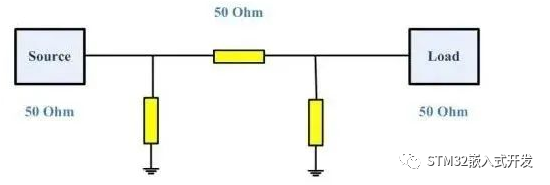
然而实际情况是：源端阻抗不会是50ohm，负载端阻抗也不会是50ohm，这个时候就需要若干个阻抗匹配电路。

而匹配电路就是由电感和电容所构成，这个时候我们就需要使用电容和电感来进行阻抗匹配电路调试，以达到RF性能最优。

阻抗匹配的方法

阻抗匹配的方法主要有两个，一是改变阻抗力，二是调整传输线。

改变阻抗力就是通过电容、电感与负载的串并联调整负载阻抗值，以达到源和负载阻抗匹配。

调整传输线是加长源和负载间的距离，配合电容和电感把阻抗力调整为零。相关文章：认识传输线的三个特性，特性阻抗、反射、阻抗匹配。

此时信号不会发生发射，能量都能被负载吸收。

高速PCB布线中，一般把数字信号的走线阻抗设计为50欧姆。一般规定同轴电缆基带50欧姆，频带75欧姆，对绞线（差分）为85-100欧姆。

阻抗匹配应用举例——振铃现象

曾经做一个项目，在电信号测量时，遇到过振铃这种问题，。

由于任何传输线都不可避免地存在着引线电阻、引线电感和杂散电容，因此，一个标准的脉冲信号在经过较长的传输线后，极易产生上冲和振铃现象。大量的实验表明，引线电阻可使脉冲的平均振幅减小；而杂散电容和引线电感的存在，则是产生上冲和振铃的根本原因。在脉冲前沿上升时间相同的条件下，引线电感越大，上冲及振铃现象就越严重；杂散电容越大，则是波形的上升时间越长；而引线电阻的增加，将使脉冲振幅减小。

如果信号传输过程中感受到阻抗的变化，就会发生信号的反射。这个信号可能是驱动端发出的信号，也可能是远端反射回来的反射信号。相关文章：信号反射问题与相关电路设计技巧。根据反射系数的公式，当信号感受到阻抗变小，就会发生负反射，反射的负电压会使信号产生下冲。信号在驱动端和远端负载之间多次反射，其结果就是信号振铃。大多数芯片的输出阻抗都很低，如果输出阻抗小于PCB走线的特性阻抗，那么在没有源端端接的情况下，必然产生信号振铃。

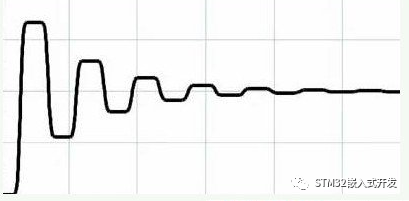
在实际电路中，采用下列几种方法来来减小和抑制上冲及振铃。

(1)串联电阻。利用具有较大电阻的传输线或是人为地串入适当的阻尼电阻，可以减小脉冲的振幅，从而达到减小上冲和振铃程度的目的。但当传入电阻的数值过大时，不仅脉冲幅度减小过多，而且使脉冲的前沿产生延迟。因此，串入的阻尼电阻值应适当，并且应选用无感电阻，电阻的连接位置应靠近接收端。

(2)减小引线电感。设法减小线路及传输线的引线电感是最基本的方法，总的原则是：

尽量缩短引线长度

加粗导线和印制铜箔的宽度

减小信号的传输距离

采用引线电感小的元器件，尤其是传输前沿很陡的脉冲信号时更应注意这些问题

(3)由于负载电路的等效电感和等效电容同样可以影响发送端，使之脉冲波形产生上冲和振铃，因此，应尽量减小负载电路的等效电感和电容。尤其是负载电路的接地线过长时，形成的地线电感和杂散电容相当可观，其影响不容忽视。

(4)逻辑数字电路中的信号线可增加上拉电阻和交流终端负载，如图6所示。上拉电阻(可取)的接入，可将信号的逻辑高电平上拉到5V。交流终端负载电路的接入不影响支流驱动能力，也不会增加信号线的负载，而高频振铃现象却可得到有效的抑制。

上述振铃除了与电路条件有关外，还与脉冲前沿的上升时间密切相关。即使电路条件相同，当脉冲前沿上升时间很短时，上冲的峰值将大大增加。一般对于前沿上升时间在1以下的脉冲，均考虑产生上冲及振铃的可能。因此，在脉冲信号频率的选择问题上，应考虑在满足系统速度要求的前提下，能选用较低频率的信号绝不选用高频信号；如无必要，也不应过分要求脉冲的前沿非常陡峭。这对从根本上消除上冲和振铃视听有利的。

Smith圆图在RF匹配电路调试中的应用

Smith圆图上可以反映出如下信息： 阻抗参数Z，导纳参数Y，品质因子Q，反射系数，驻波系数，噪声系数，增益，稳定因子，功率，效率，频率信息等抗等参数。

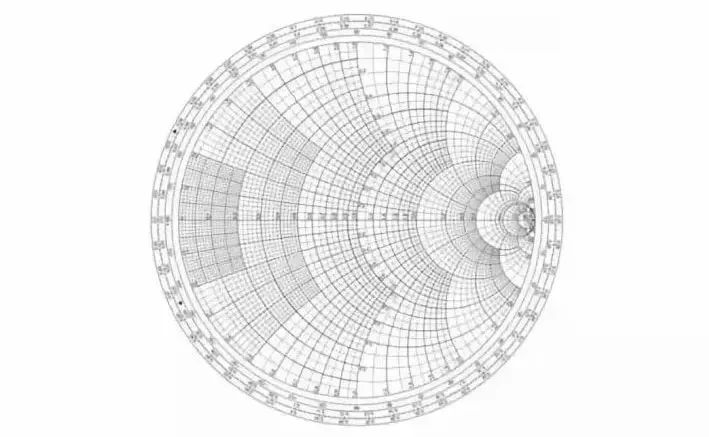
是不是一脸懵，我们还是来看阻抗圆图吧：

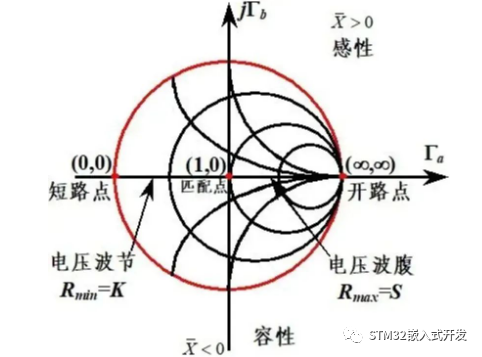
阻抗圆图的构图原理是利用输入阻抗与电压反射系数之间的一一对应关系，将归一化输入阻抗表示在反射系数极坐标系中，其特点归纳如下：

上半圆阻抗为感抗，下半圆阻抗为容抗

实轴为纯电阻，单位圆为纯电抗

实轴的右半轴皆为电压波腹点（除开路点），左半轴皆为电压波节点（除短路点）

匹配点（1，0），开路点（∞，∞）和短路点（0，0）

两个特殊圆:最大的为纯电抗圆，与虚轴相切的为匹配圆

两个旋转方向:逆时针转为向负载移动，顺时针转为向波源移动

导纳圆图与阻抗圆图互为中心对称，同一张圆图，即可以当作阻抗圆图来用，也可以当作导纳圆图来用，但是在进行每一次操作时，若作为阻抗圆图用则不能作为导纳圆图。

Smith圆图中，能表示出一些很有意思的特征：

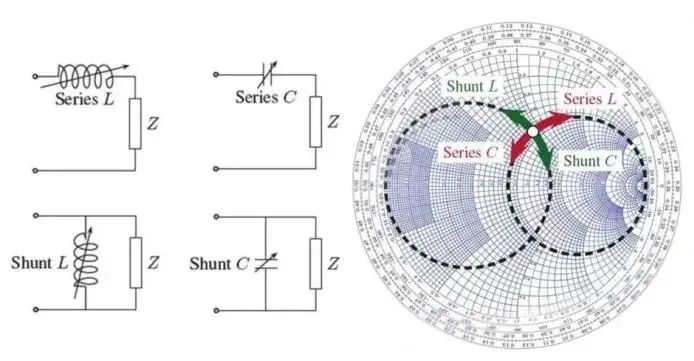
在负载之前串联或并联一个可变电感/电容，电路图如下图左侧4个图所示，将得到Smith圆图上右侧的几条曲线。

对应Smith阻抗圆及导纳圆，其运动轨迹如下：

使用Smith阻抗圆时，串联电感顺时针转，串联电容逆时针转

使用Smith导纳圆时，并联电感，逆时针转，并联电容顺时针转

审核编辑 ：李倩