

公式推导过程是理解SVPWM的关键
描述
转眼间已到了毕业第八个年头,一直在学习、一直在钻研、也一直在成长,只因这是自己喜欢的工作。以技术立身,累并快乐着。
最近一段时间因为工作需要开始研究SVPWM调制,有了一些心得给大家分享。SVPWM比较难以理解,个人认为公式的推导过程是理解SVPWM的关键,扇区分配一定要亲自去画矢量图,对理解很有帮助。
1、旋转矢量的合成
为什么要进行矢量合成?正常来说三相就应该控制三个量,三个量很难控制,但是三个量之间存在关系,所以我们可以把它们合成一个量控制。
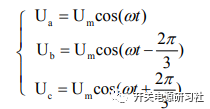
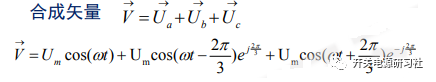
根据欧拉公式: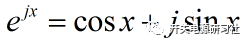 带入上式得
带入上式得
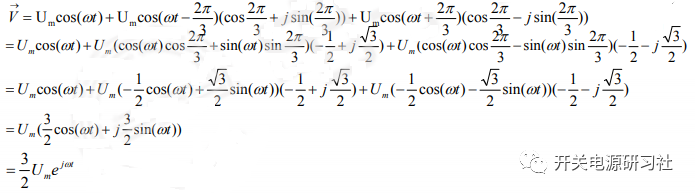
这个公式会在各种相关论文上重复出现。三相合成矢量角速度为wt,幅值为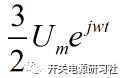 .
.
2、Clark变换与Park变换
逆变器三相输出电压为:
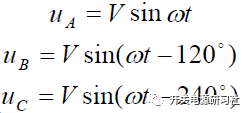
将上面式子展开可以得到:
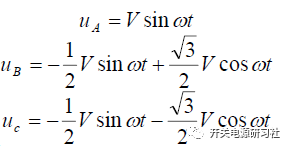
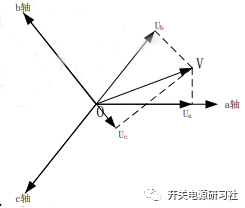
如果是在静止坐标系的情况下,那么在中间旋转的电压矢量V在静止坐标系αβ 里面的投影分别为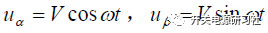 ,
,
进行矩阵变换:
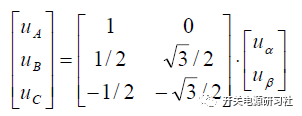
进行矩阵逆变换:
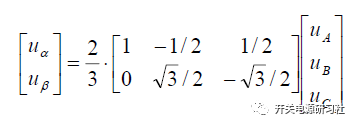
将dq 旋转坐标系转换到静止坐标系αβ 之中:
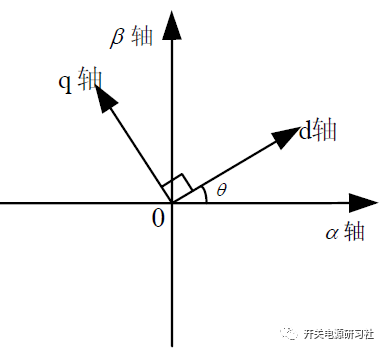
在两相旋转坐标系的情况下,中间旋转的电压矢量V在两相同步旋转坐标系dq 里面的投影分别为:
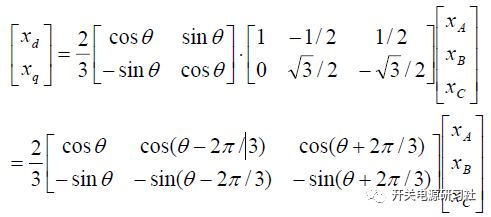
空间电压矢量V的顶点的轨迹是一个圆,圆相应的半径为相电压幅值的1.5 倍。那么空间电压矢量的轨迹越接近圆,也就意味着三相输出相电压越接近于三相对称正弦波,所以使逆变器输出的空间电压矢量顶点的运动轨迹越接近一个标准圆,输出相电压的波形也就越好。通过空间矢量变换,使三个标量的控制问题转化成了一个矢量的控制问题。
3、扇区划分
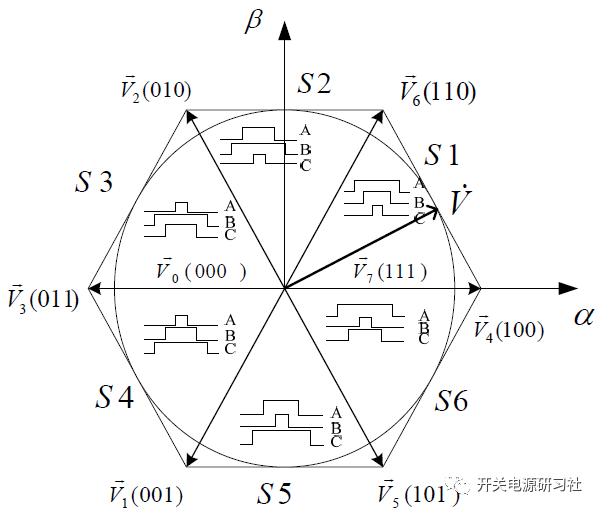
先来看第一扇区满足的条件,首先是在第一象限,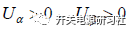 ,其次
,其次
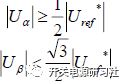
其中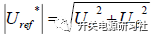 ,进一步简化关系,这个公式可以简化成,
,进一步简化关系,这个公式可以简化成,
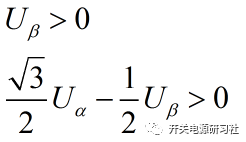
其它扇区依此类推,可以得到相应关系如下:
在第二扇区的时候:
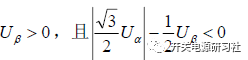
在第三扇区的时候:
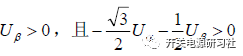
在第四扇区的时候:
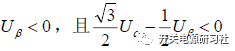
在第五扇区的时候:
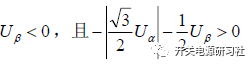
在第六扇区的时候:
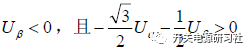
分析上面的结果,可以很明显的看出来,如果想知道在哪个扇区,我们完全可以根据上面三个式子与零的关系来推理得到。
如果他们大于零的话,用1来表示,小于零的话用0来表示。并且用A、B、C 来对应相应的逻辑值,即如下所示:
如果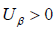 ,那么A =1,否则A = 0
,那么A =1,否则A = 0
如果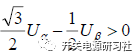 ,那么B = 1,否则B = 0
,那么B = 1,否则B = 0
如果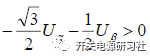 ,那么C = 1,否则C = 0
,那么C = 1,否则C = 0
令N = A + 2B + 4C,这个也好理解,对应着二进制001、010、100,
这样每一个N 就对应着一个扇区,计算出相应结果,对应的表格如下所示:

这种方法判断扇区比较简单,具体分配扇区的时候将计算出来的N 值与实际扇区号对应起来就可以了。
4、扇区矢量时间计算
以第一扇区为例:
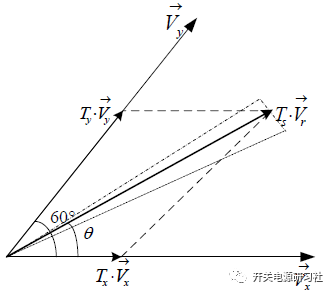
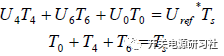
用αβ 坐标系来描述上面的公式,那么可以得到:
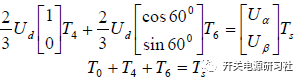
解出上面的关系式可以得到:
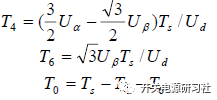
用同样的方法可以得到在其它扇区各个适量的作用时间:

我们定义:
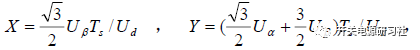
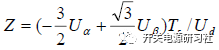
那么相关的赋值可以单独算出 X,Y,Z 既可,然后给他们分配给相应的扇区。时间分配就变为:

最终得到每个采样周期中各矢量切换点的数值,将他们与一定频率和幅度的三角载波进行相应的比较,这样就完成了SVPWM变换。
审核编辑:何安
-
AS2S1210环路公式的具体推导过程是怎样的?2023-12-04 423
-
SVPWM的原理及法则推导和控制算法介绍2023-10-07 859
-
基于载波SVPWM与空间矢量SVPWM实现策略的等效推导2023-07-10 3574
-
基于Mathcad的LLC公式推导与化简(2)2023-06-23 7961
-
电机控制---SVPWM扇区判断的实现以及推导过程2023-05-05 1129
-
LLC变换器公式的推导2023-04-03 698
-
svpwm是干什么的2022-01-13 1128
-
LLC增益曲线过程推导和参数如何计算2020-05-19 19749
-
反激公式推导及GU10原边反馈LED方案设计过程2019-12-09 1152
-
动能定理公式的理解与推导2018-03-16 42517
-
SVPWM的原理及法则推导和控制算法详解2016-04-13 895
-
SVPWM的原理推导和控制算法详解2016-01-28 14011
-
Aw,XAc计算公式的推导2009-02-19 3152
全部0条评论

快来发表一下你的评论吧 !

