如何将前中后序的递归框架改写成迭代形式

算法与数据结构 2022-03-18 1143

描述

之前经常讲涉及递归的算法题，我说过写递归算法的一个技巧就是不要试图跳进递归细节，而是从递归框架上思考，从函数定义去理解递归函数到底该怎么实现。

而且我们前文学习数据结构和算法的框架思维特别强调过，练习递归的框架思维最好方式就是从二叉树相关题目开始刷，前文也有好几篇手把手带你刷二叉树和二叉搜索树的文章：

之前的文章全部都是运用二叉树的递归框架，帮你透过现象看本质，明白二叉树的各种题目本质都是前中后序遍历衍生出来的。

前文 BFS 算法框架详解是利用队列迭代地遍历二叉树，不过使用的是层级遍历，没有递归遍历中的前中后序之分。

由于现在面试越来越卷，很多读者在后台问我如何将前中后序的递归框架改写成迭代形式。

首先我想说，递归改迭代从实用性的角度讲是没什么意义的，明明可以写递归解法，为什么非要改成迭代的方式？

对于二叉树来说，递归解法是最容易理解的，非要让你改成迭代，顶多是考察你对递归和栈的理解程度，架不住大家问，那就总结一下吧。

我以前见过一些迭代实现二叉树前中后序遍历的代码模板，比较短小，容易记，但通用性较差。

通用性较差的意思是说，模板只是针对「用迭代的方式返回二叉树前/中/后序的遍历结果」这个问题，函数签名类似这样，返回一个TreeNode列表：

List traverse(TreeNode root);

如果给一些稍微复杂的二叉树问题，比如最近公共祖先，二叉搜索子树的最大键值和，想把这些递归解法改成迭代，就无能为力了。

而我想要的是一个万能的模板，可以把一切二叉树递归算法都改成迭代。

换句话说，类似二叉树的递归框架：

void traverse(TreeNode root) {
    if (root == null) return;
    /* 前序遍历代码位置 */
    traverse(root.left);
    /* 中序遍历代码位置 */
    traverse(root.right);
    /* 后序遍历代码位置 */
}

迭代框架也应该有前中后序代码的位置：

void traverse(TreeNode root) {
    while (...) {
        if (...) {
          /* 前序遍历代码位置 */
        }
        if (...) {
          /* 中序遍历代码位置 */
        }
        if (...) {
          /* 后序遍历代码位置 */
        }
    }
}

我如果想把任何一道二叉树递归解法改成迭代，直接把递归解法中前中后序对应位置的代码复制粘贴到迭代框架里，就可以直接运行，得到正确的结果。

理论上，所有递归算法都可以利用栈改成迭代的形式，因为计算机本质上就是借助栈来迭代地执行递归函数的。

所以本文就来利用「栈」模拟函数递归的过程，总结一套二叉树通用迭代遍历框架。

递归框架改为迭代

参加过我的二叉树专项训练的读者应该知道，二叉树的递归框架中，前中后序遍历位置就是几个特殊的时间点：

前序遍历位置的代码，会在刚遍历到当前节点root，遍历root的左右子树之前执行；

中序遍历位置的代码，会在在遍历完当前节点root的左子树，即将开始遍历root的右子树的时候执行；

后序遍历位置的代码，会在遍历完以当前节点root为根的整棵子树之后执行。

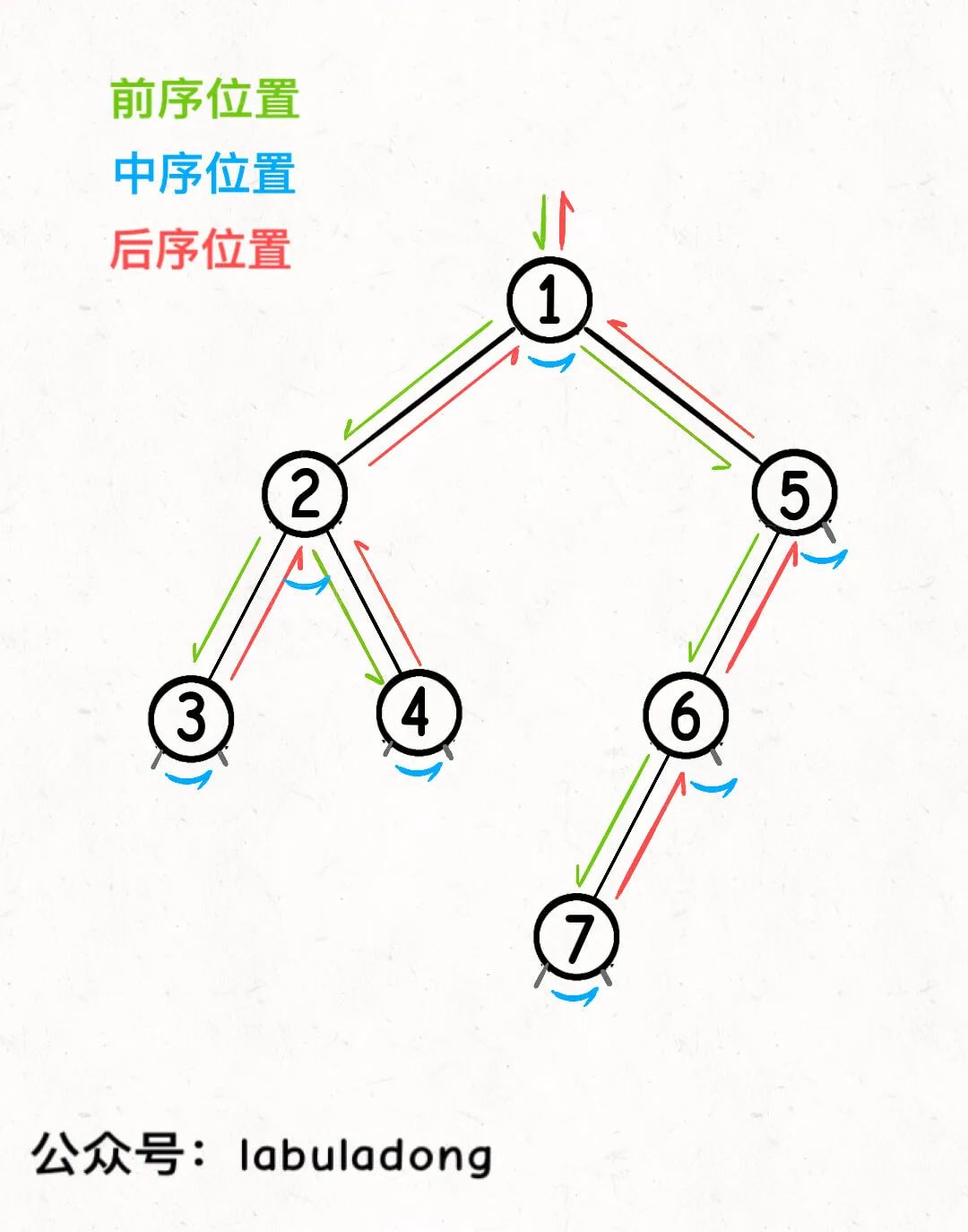
如果从递归代码上来看，上述结论是很容易理解的：

void traverse(TreeNode root) {
    if (root == null) return;
    /* 前序遍历代码位置 */
    traverse(root.left);
    /* 中序遍历代码位置 */
    traverse(root.right);
    /* 后序遍历代码位置 */
}

不过，如果我们想将递归算法改为迭代算法，就不能从框架上理解算法的逻辑，而要深入细节，思考计算机是如何进行递归的。

假设计算机运行函数A，就会把A放到调用栈里面，如果A又调用了函数B，则把B压在A上面，如果B又调用了C，那就再把C压到B上面……

当C执行结束后，C出栈，返回值传给B，B执行完后出栈，返回值传给A，最后等A执行完，返回结果并出栈，此时调用栈为空，整个函数调用链结束。

我们递归遍历二叉树的函数也是一样的，当函数被调用时，被压入调用栈，当函数结束时，从调用栈中弹出。

那么我们可以写出下面这段代码模拟递归调用的过程：

// 模拟系统的函数调用栈
Stack stk = new Stack<>();

void traverse(TreeNode root) {
    if (root == null) return;
    // 函数开始时压入调用栈
    stk.push(root);
    traverse(root.left);
    traverse(root.right);
    // 函数结束时离开调用栈
    stk.pop();
}

如果在前序遍历的位置入栈，后序遍历的位置出栈，stk中的节点变化情况就反映了traverse函数的递归过程（绿色节点就是被压入栈中的节点，灰色节点就是弹出栈的节点）：

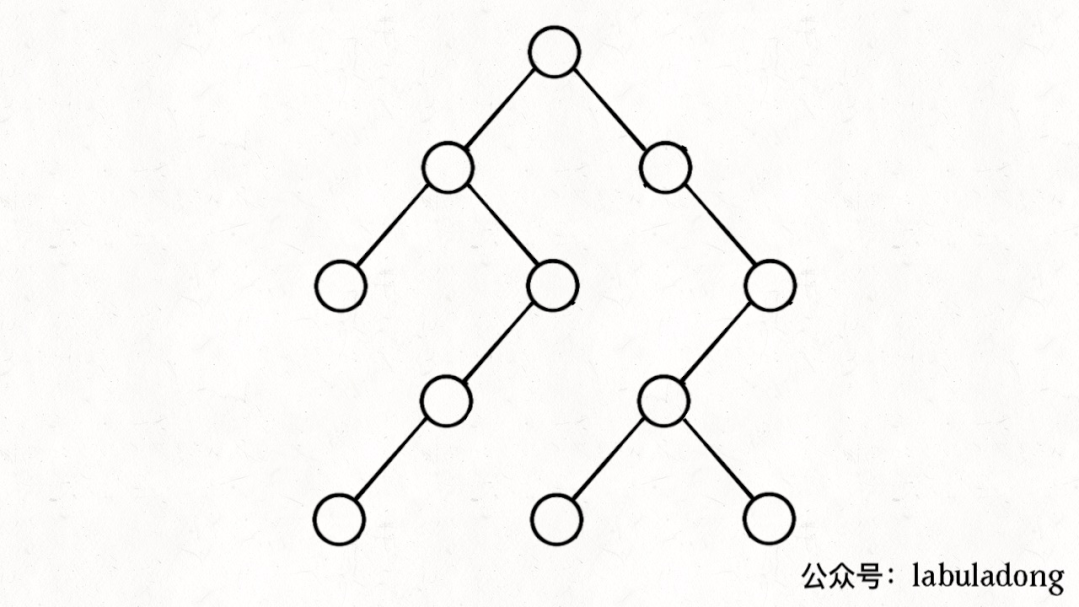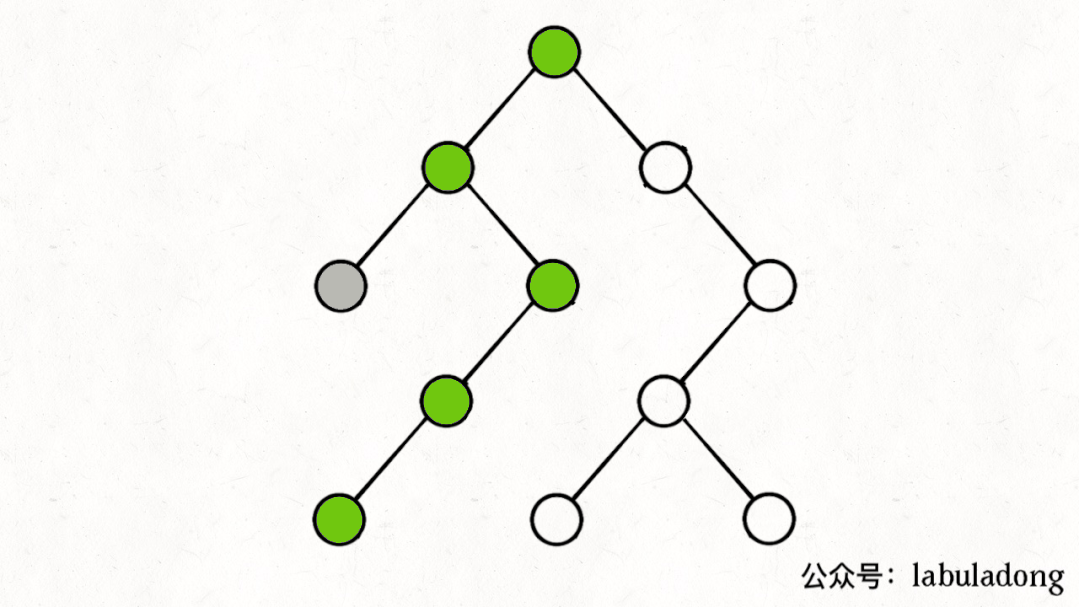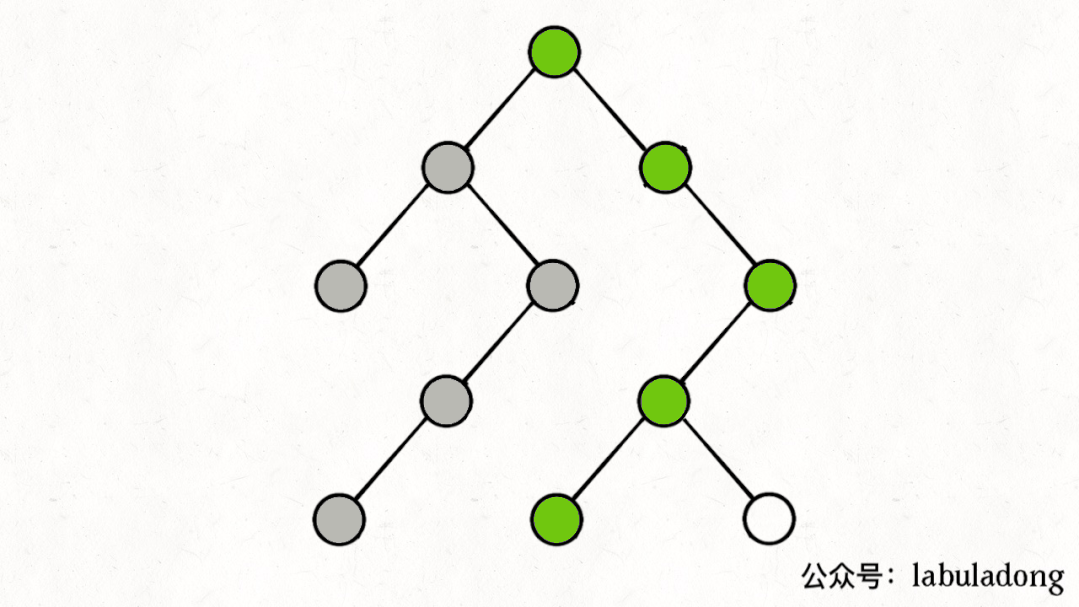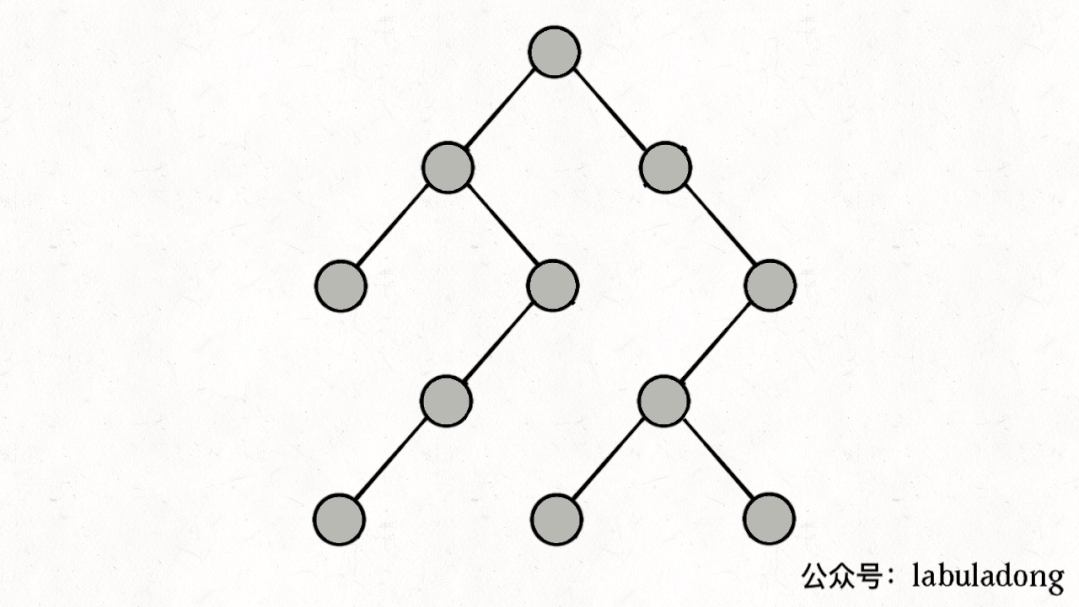
简单说就是这样一个流程：

1、拿到一个节点，就一路向左遍历（因为traverse(root.left)排在前面），把路上的节点都压到栈里。

2、往左走到头之后就开始退栈，看看栈顶节点的右指针，非空的话就重复第 1 步。

写成迭代代码就是这样：

private Stack stk = new Stack<>();

public List traverse(TreeNode root) {
    pushLeftBranch(root);

    while (!stk.isEmpty()) {
        TreeNode p = stk.pop();
        pushLeftBranch(p.right);
    }
}

// 左侧树枝一撸到底，都放入栈中
private void pushLeftBranch(TreeNode p) {
    while (p != null) {
        stk.push(p);
        p = p.left;
    }
}

上述代码虽然已经可以模拟出递归函数的运行过程，不过还没有找到递归代码中的前中后序代码位置，所以需要进一步修改。

迭代代码框架

想在迭代代码中体现前中后序遍历，关键点在哪里？

当我从栈中拿出一个节点p，我应该想办法搞清楚这个节点p左右子树的遍历情况。

如果p的左右子树都没有被遍历，那么现在对p进行操作就属于前序遍历代码。

如果p的左子树被遍历过了，而右子树没有被遍历过，那么现在对p进行操作就属于中序遍历代码。

如果p的左右子树都被遍历过了，那么现在对p进行操作就属于后序遍历代码。

上述逻辑写成伪码如下：

private Stack stk = new Stack<>();

public List traverse(TreeNode root) {
    pushLeftBranch(root);

    while (!stk.isEmpty()) {
        TreeNode p = stk.peek();

        if (p 的左子树被遍历完了) {
            /*******************/
            /** 中序遍历代码位置 **/
            /*******************/
            // 去遍历 p 的右子树
            pushLeftBranch(p.right);
        }

        if (p 的右子树被遍历完了) {
            /*******************/
            /** 后序遍历代码位置 **/
            /*******************/
            // 以 p 为根的树遍历完了，出栈
            stk.pop();
        }
    }
}

private void pushLeftBranch(TreeNode p) {
    while (p != null) {
        /*******************/
        /** 前序遍历代码位置 **/
        /*******************/
        stk.push(p);
        p = p.left;
    }
}

有刚才的铺垫，这段代码应该是不难理解的，关键是如何判断p的左右子树到底被遍历过没有呢？

其实很简单，我们只需要维护一个visited指针，指向「上一次遍历完成的根节点」，就可以判断p的左右子树遍历情况了

下面是迭代遍历二叉树的完整代码框架：

// 模拟函数调用栈
private Stack stk = new Stack<>();

// 左侧树枝一撸到底
private void pushLeftBranch(TreeNode p) {
    while (p != null) {
        /*******************/
        /** 前序遍历代码位置 **/
        /*******************/
        stk.push(p);
        p = p.left;
    }
}

public List traverse(TreeNode root) {
    // 指向上一次遍历完的子树根节点
    TreeNode visited = new TreeNode(-1);
    // 开始遍历整棵树
    pushLeftBranch(root);

    while (!stk.isEmpty()) {
        TreeNode p = stk.peek();

        // p 的左子树被遍历完了，且右子树没有被遍历过
        if ((p.left == null || p.left == visited) 
          && p.right != visited) {
            /*******************/
            /** 中序遍历代码位置 **/
            /*******************/
            // 去遍历 p 的右子树
            pushLeftBranch(p.right);
        }
        // p 的右子树被遍历完了
        if (p.right == null || p.right == visited) {
            /*******************/
            /** 后序遍历代码位置 **/
            /*******************/
            // 以 p 为根的子树被遍历完了，出栈
            // visited 指针指向 p
            visited = stk.pop();
        }
    }
}

代码中最有技巧性的是这个visited指针，它记录最近一次遍历完的子树根节点（最近一次 pop 出栈的节点），我们可以根据对比p的左右指针和visited是否相同来判断节点p的左右子树是否被遍历过，进而分离出前中后序的代码位置。

PS：visited指针初始化指向一个新 new 出来的二叉树节点，相当于一个特殊值，目的是避免和输入二叉树中的节点重复。

只需把递归算法中的前中后序位置的代码复制粘贴到上述框架的对应位置，就可以把任意递归的二叉树算法改写成迭代形式了。

比如，让你返回二叉树后序遍历的结果，你就可以这样写：

private Stack stk = new Stack<>();

public List postorderTraversal(TreeNode root) {
    // 记录后序遍历的结果
    List postorder = new ArrayList<>();
    TreeNode visited = new TreeNode(-1);

    pushLeftBranch(root);
    while (!stk.isEmpty()) {
        TreeNode p = stk.peek();

        if ((p.left == null || p.left == visited) 
          && p.right != visited) {
            pushLeftBranch(p.right);
        }

        if (p.right == null || p.right == visited) {
            // 后序遍历代码位置
            postorder.add(p.val);
            visited = stk.pop();
        }
    }

    return postorder;
}

private void pushLeftBranch(TreeNode p) {
    while (p != null) {
        stk.push(p);
        p = p.left;
    }
}

当然，任何一个二叉树的算法，如果你想把递归改成迭代，都可以套用这个框架，只要把递归的前中后序位置的代码对应过来就行了。

迭代解法到这里就搞定了，不过我还是想强调，除了 BFS 层级遍历之外，二叉树的题目还是用递归的方式来做，因为递归是最符合二叉树结构特点的。

说到底，这个迭代解法就是在用栈模拟递归调用，所以对照着递归解法，应该不难理解和记忆。

原文标题：二叉树八股文：递归改迭代通用模板

文章出处：【微信公众号：算法与数据结构】欢迎添加关注！文章转载请注明出处。

审核编辑：汤梓红

打开APP阅读更多精彩内容