如何使用 go 实现红黑树

本文介绍了使用 go 实现红黑树。

二叉搜索树（二叉查找树）

二叉查找树也叫二叉搜索树，也叫二叉排序树，它具有以下特点：1. 如果左子树不为空，则左子树上的结点的值都小于根节点；2. 如果右子树不为空，则右子树上的结点的值都大于根节点；3. 子树同样也要遵循以上两点。

二叉树的遍历方式

二叉树的遍历方式：前序遍历、中序遍历、后序遍历和层序遍历（MySql）。

只要一棵树是二叉查找树，那么它的中序遍历（左根右输出）一定是有序的。比如看下边的一棵二叉树：

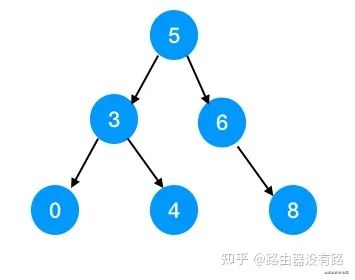
它的前序遍历（根左右）为：530468；
它的中序遍历（左根右）为：034568；
它的后序遍历（左右根）为：043865。

二叉搜索树有哪些应用？

既然是搜索树，那么它肯定就是用在查找上。我们来分析下它的查找时间复杂度：

先来看下面两颗二叉搜索树：

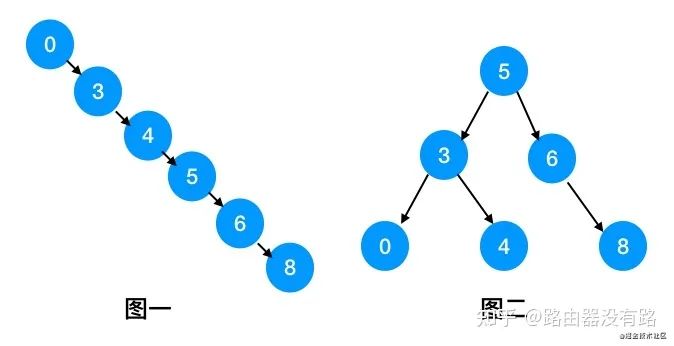
查找时间复杂度其实就是树的深度。

上图一的时间复杂度：O(n)时间复杂度，表示需要查找 n 次，即循环 n 遍，退化成链表的情况。

上图二的时间复杂度（类似二分查找）：logn，即 => x= => logn。

那么为什么会出现退化成链表的情况（图一）呢？我们该怎么处理才不会变成链表呢（怎么解决）？

当插入的节点数值从小到大时，则就会出现二叉树退化成链表的情况，那么有另一种树可以解决这种情况，就是平衡二叉树（AVL树）。

AVL树是一种追求极致平衡的二叉搜索树，即将树调整到最优的情况，由于这种树结构比较苛刻、旋转也比较多，这里就不重点展开讲。

红黑树

红黑树的由来

今天需要重点讲的是红黑树。红黑树的底层数据结构其实就是二叉查找树，也就是说红黑树是一颗特殊的二叉查找树，也叫自平衡二叉查找树。

红黑树出现的目的就是上所讲到的，为了解决二叉树退化成链表的情况。

红黑树的演进过程

链表(暴力查处) -> 二叉树 -> 二叉查找树 -> 特殊的二叉查找树(自平衡的二叉查找树)

红黑色讲解

通过上面的例子以及两个图，我们发现二叉树的结构就决定了其搜索的效率及性能，那么我们需要怎么样才让二叉树达到优化的效果呢？

因此就有了红黑树了，我们看下图（红黑树）：

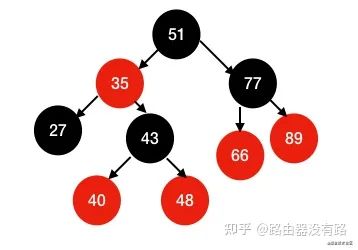
红黑树的性质：

每个节点不是红色就是黑色（这里不一定要红色和黑色，只要知道这里的红色和黑色是什么意思即可）

一定没有连在一起的红色节点

根节点（第一个节点）是黑色 root

每个红色节点的两个字节点都是黑色

叶子结点都是黑色（上图中其实还有为null的叶子结点没有画出来），如下图所示：

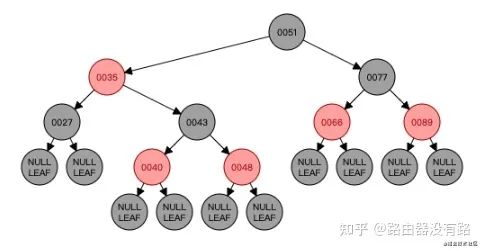
根据以上性质或者说满足了以上性质的树，就可以达到近似平衡了。

怎么判断一个节点是否为根结点？

没有父节点

入度为0的节点

红黑树变换规则

要满足这些性质，需要对树做什么操作呢？

为了红黑可以满足这些性质，因此出现了旋转，那么红黑树有几种变换规则呢？

有三种变换规则：

变色：红变黑 黑变红

左旋转

右旋转

左旋转示例：

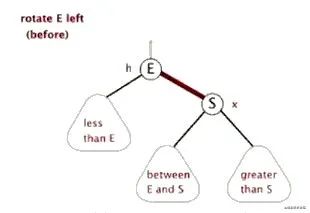
旋转和颜色变换规则：所有插入的点默认为红色； 1. 变颜色的情况：如果插入的节点的父节点和叔叔节点为红色，则：1）把父节点和叔叔节点设为黑色；2）把爷爷(祖父)节点设为红色；3）把指针定位到爷爷节点作为当前需要操作的节点，再根据变换规则来进行判断操作。2. 左旋：如果当前父节点是红色，叔叔节点是黑色，而且当前的节点是右子树时，则需要以父节点作为左旋转。3. 右旋：当前父节点是红色，叔叔节点是黑色，且当前的节点是左子树时，则：1）把父节点变为黑色；2）把爷爷节点变为红色；3）以父节点右旋转。

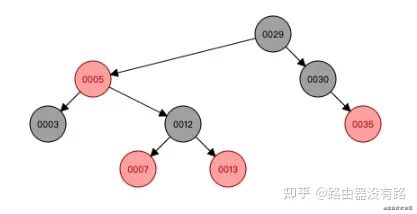
比如要往上图中插入数字6，则这颗红黑色的演变过程如下：

step1: 插入6节点后如下图，它的父节点和叔叔节点均是红色，则需要根据变换规则来操作，到step2了。

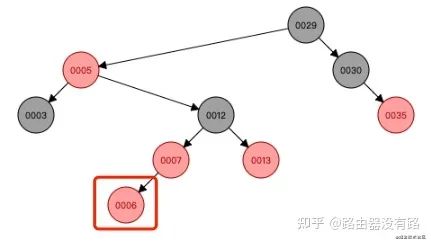
step2: 根据变换规则，需要将插入节点的父节点和叔叔节点均变为黑色，爷爷节点变为红色，然后将指针定位到爷爷节点(蓝色圈)。将指针定位到爷爷节点(12)后，此时做为当前需要操作的节点，再根据变换规则来判断，可以看到下图的当前节点(12)的叔叔节点是黑色的，则不能用变颜色规则的情况了，进行step3，此时需要进行左旋或右旋了。

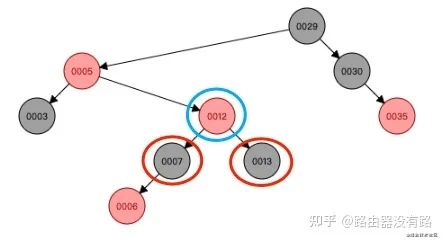
step3: 根据上图情况可以知道此时是符合左旋规则的：当前节点(12)的父节点(5)是红色，叔叔节点(3)是黑色，而且当前的节点是右子树。接下来需要进行左旋变换(三步走)：

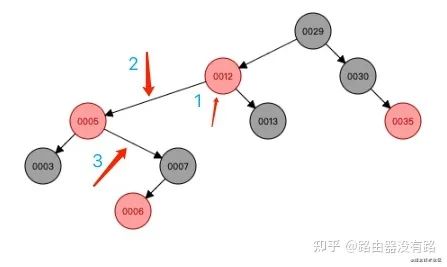
step4：左旋变换后，可以看到当前节点(5)的父节点(12)为红色，叔叔节点(30)为黑色，而且当前节点为左子树，符合右旋的规则。接下来就是进行右旋的变换操作了：1）把父节点(12)变为黑色；2）把爷爷节点(29)变为红色；3）以父节点(12)右旋转

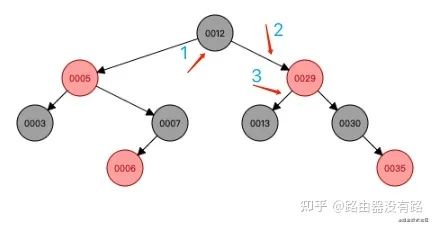
小结

到这里，可以看到经过多次旋转后，这棵树是符合红黑色的性质。

Golang代码实现红黑树

直接上代码，如下：

 

package main

import (
    "fmt"
    "math/rand"
    "time"
)

const (
    RED bool = true
    BLACK bool = false
)

type Node struct {
    key int
    value interface{}

    left *Node
    right *Node
    //parent *Node

    color bool
}

type RedBlackTree struct {
    size int
    root *Node
}

func NewNode(key, val int) *Node {
    // 默认添加红节点
    return &Node{
        key:    key,
        value:  val,
        left:   nil,
        right:  nil,
        //parent: nil,
        color:  RED,
    }
}

func NewRedBlackTree() *RedBlackTree {
    return &RedBlackTree{}
}

func (n *Node) IsRed() bool {
    if n == nil {
        return BLACK
    }
    return n.color
}

func (tree *RedBlackTree) GetTreeSize() int {
    return tree.size
}

//   node                     x
//  /        左旋转         /  
// T1   x   --------->   node   T3
//     /               /   
//    T2 T3            T1   T2
func (n *Node) leftRotate() *Node {
    // 左旋转
    retNode := n.right
    n.right = retNode.left

    retNode.left = n
    retNode.color = n.color
    n.color = RED

    return retNode
}

//     node                    x
//    /        右旋转       /  
//   x    T2   ------->   y   node
//  /                        /  
// y  T1                     T1  T2
func (n *Node) rightRotate() *Node {
    //右旋转
    retNode := n.left
    n.left = retNode.right

    retNode.right = n
    retNode.color = n.color
    n.color = RED

    return retNode
}

// 颜色变换
func (n *Node) flipColors() {
    n.color = RED
    n.left.color = BLACK
    n.right.color = BLACK
}

// 维护红黑树
func (n *Node) updateRedBlackTree(isAdd int) *Node {
    // isAdd=0 说明没有新节点，无需维护
    if isAdd == 0 {
        return n
    }

    // 需要维护
    if n.right.IsRed() == RED && n.left.IsRed() != RED {
        n = n.leftRotate()
    }

    // 判断是否为情形3，是需要右旋转
    if n.left.IsRed() == RED && n.left.left.IsRed() == RED {
        n = n.rightRotate()
    }

    // 判断是否为情形4，是需要颜色翻转
    if n.left.IsRed() == RED && n.right.IsRed() == RED {
        n.flipColors()
    }

    return n
}

// 递归写法:向树的root节点中插入key,val
// 返回1, 代表加了节点
// 返回0, 代表没有添加新节点, 只更新key对应的value值
func (n *Node) add(key, val int) (int, *Node) {
    if n == nil {   // 默认插入红色节点
        return 1, NewNode(key, val)
    }

    isAdd := 0
    if key < n.key {
        isAdd, n.left = n.left.add(key, val)
    } else if key > n.key {
        isAdd, n.right = n.right.add(key, val)
    } else {
        // 对value值更新,节点数量不增加,isAdd = 0
        n.value = val
    }

    // 维护红黑树
    n = n.updateRedBlackTree(isAdd)

    return isAdd, n
}

func (tree *RedBlackTree) Add(key, val int)  {
    isAdd, nd := tree.root.add(key, val)
    tree.size += isAdd
    tree.root = nd
    tree.root.color = BLACK //根节点为黑色节点
}

// 前序遍历打印出key,val,color
func (tree *RedBlackTree) PrintPreOrder() {
    resp := make([][]interface{}, 0)
    tree.root.printPreOrder(&resp)
    fmt.Println(resp)
}

func (n *Node) printPreOrder(resp *[][]interface{}) {
    if n == nil {
        return
    }
    *resp = append(*resp, []interface{}{n.key, n.value, n.color})
    n.left.printPreOrder(resp)
    n.right.printPreOrder(resp)
}


// 测试红黑树代码
func main() {
    count := 10
    redBlackTree := NewRedBlackTree()
    nums := make([]int, 0)
    for i := 0; i < count; i++ {
        nums = append(nums, rand.Intn(count))
    }

    fmt.Println("source data: ", nums)
    now := time.Now()
    for _, v := range nums {
        redBlackTree.Add(v, v)
    }

    fmt.Println("redBlackTree:", now.Sub(time.Now()))
    redBlackTree.PrintPreOrder()
    fmt.Println("节点数量:", redBlackTree.GetTreeSize())
}

 

测试输出结果如下：

 

data source: [1 7 7 9 1 8 5 0 6 0]
redBlackTree: -2.136µs
[[7 7 false] [1 1 true] [0 0 false] [6 6 false] [5 5 true] [9 9 false] [8 8 true]]
节点数量: 7

 

总结

红黑树是保持近似平衡的二叉树，从另一种角度上来说红黑树不是平衡二叉树，它的最大高度为2*logn。

二分搜索树，AVL树，红黑树对比：1. 对于完全随机的数据源，普通二分搜索树很好用，缺陷是在极端情况下容易退化成链表 2. 对于查询较多的使用情况，AVL树很好用，因为他的高度一直保持h=logn 3. 红黑树牺牲了平衡性，即h=2*logn，但在添加和删除操作中，红黑树比AVL树有优势 4. 综合增删改查所有操作，红黑树的统计性能更优

原文标题：二叉树、红黑树以及Golang实现红黑树

文章出处：【微信公众号：Linux爱好者】欢迎添加关注！文章转载请注明出处。

　　审核编辑：彭菁