

数据挖掘实战:金融贷款分类模型和时间序列分析
描述
今天给大家带来一个企业级数据挖掘实战项目,金融贷款分类模型和时间序列分析,文章较长,建议收藏!
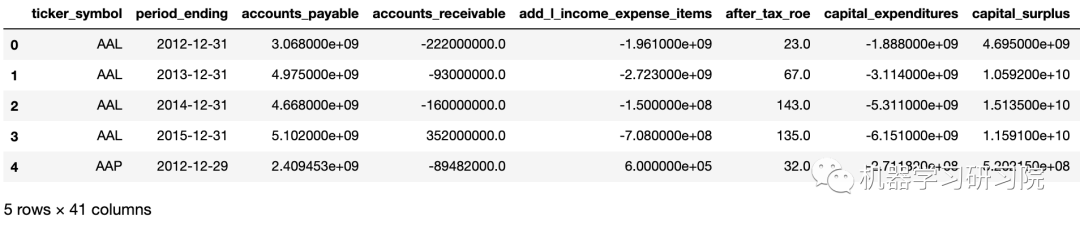
 只保留所有公司去年的数据。我们将只考虑最新的数据,并在原始数据集中添加破产的预测值。
只保留所有公司去年的数据。我们将只考虑最新的数据,并在原始数据集中添加破产的预测值。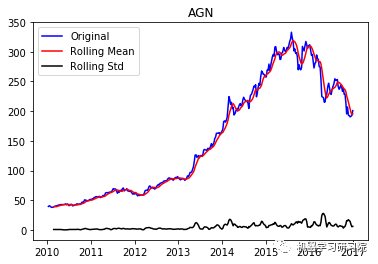
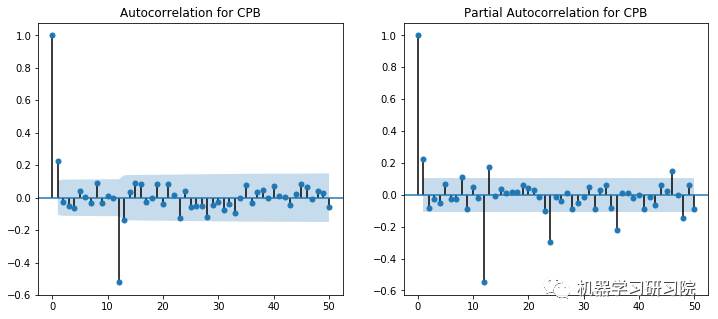
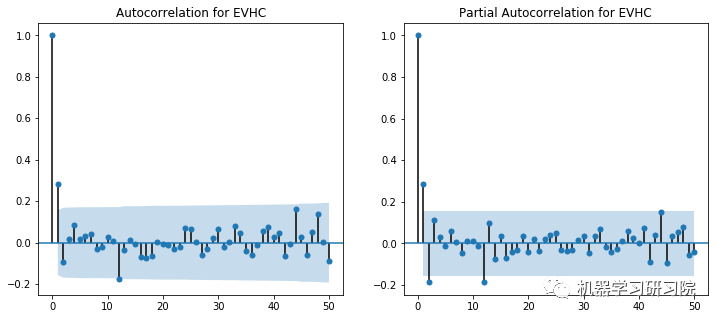
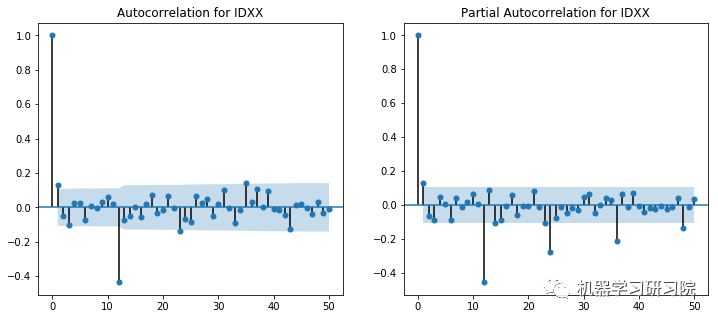 ACF和PACF图显示在滞后1时出现峰值。然而,这些图本身并不是决定性的,因为没有一个可以说是指数下降的,当然,也显示了一些异常值。使用不同p和q值的试验在(2,1)处显示出显著更好的结果。
对所有公司进行ACF-PACF分析是不可能的,因此对于SVD不收敛于(2,1)的实例,使用了(1,0)的回退值。
ACF和PACF图显示在滞后1时出现峰值。然而,这些图本身并不是决定性的,因为没有一个可以说是指数下降的,当然,也显示了一些异常值。使用不同p和q值的试验在(2,1)处显示出显著更好的结果。
对所有公司进行ACF-PACF分析是不可能的,因此对于SVD不收敛于(2,1)的实例,使用了(1,0)的回退值。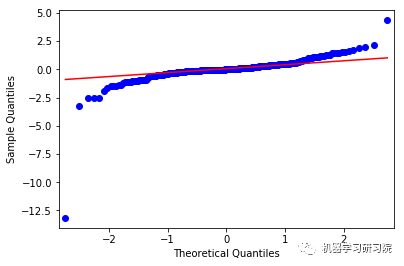
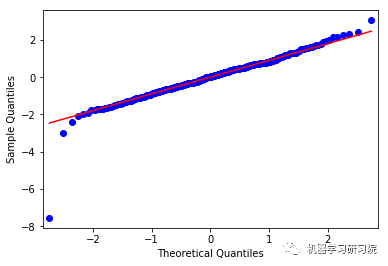
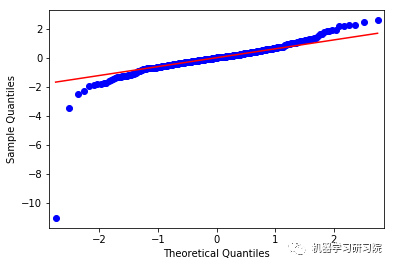
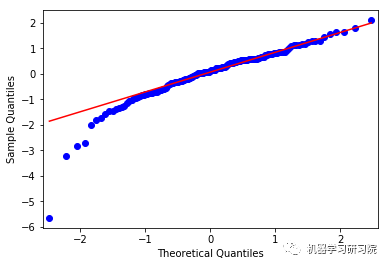
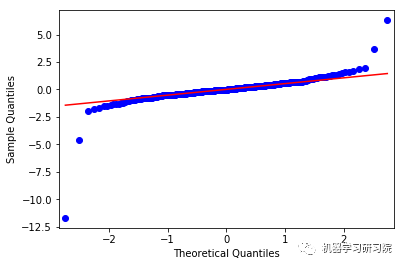 上面这些图显示了合理的平等分布,因此我们可以得出结论,残差分析是适当的。
时间序列模型分析。
上面这些图显示了合理的平等分布,因此我们可以得出结论,残差分析是适当的。
时间序列模型分析。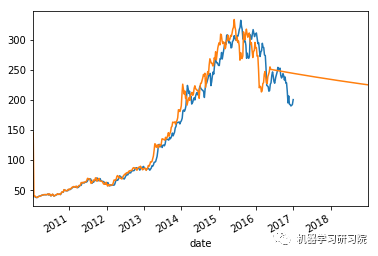
 生成一个混淆矩阵并计算Matthews相关系数作为训练的随机森林分类器的评估指标。
生成一个混淆矩阵并计算Matthews相关系数作为训练的随机森林分类器的评估指标。
项目背景
银行和其他金融贷款机构经常需要查看贷款申请人的信用历史、经济状况和其他因素,以确定贷款资格,但这些因素之间的关系通常不是明确定义的,但在本质上可以得到启发的。通常情况下,公司近况,如其近期的兴衰,也被作为决定其财务稳定性的考虑因素。因为这些因素考虑不当,或者被忽略了。这很可能会导致对公司拖欠贷款可能性的判断错误。 因此,我们可以使用有效的分类和时间序列分析,生成一个好的模型,不仅会更精确,而且会大大降低在解决这个问题上的成本效益。有了这个目标,我们将分析数据,并用来自其他集合的数据来补充它,并通过创建分类策略和分析模型所采取的步骤,试图理解与公司财务状况相关度最高的静态因素。目标变量和预测变量
我们总共使用了42个特征来确定最终分类器中的目标,目标本身是由SVM分类器输出和ARIMA时间序列分析得到的复合变量。 使用的最重要的预测变量是:Accounts Payable, Capital Expenditures, Additional Income Expense Items, Accounts Receivable and After Tax Return on Equity(应付帐款、资本支出、额外收入费用项目、应收帐款和税后权益回报)。
目标变量是公司股票价格在两年内的变化百分比和公司在未来4年内破产的可能性的总和。问题陈述
识别各种静态特征,这些特征负责确定公司的增长趋势,从而确定其获得贷款的资格。模型的类型
这些数据集包括申请破产的公司的数据、纽约证券交易所组织的6年股票趋势和这些公司的财务数据。我们在破产公司数据集上尝试了多种模型,包括决策树、线性模型和Logistic回归,并得出基于AUC值的支持向量机最适合于该数据集的结论。 采用ARIMA时间序列方法对股票走势进行了分析。使用这些值将一个复合标签添加到金融数据集中,最后在这个数据集上使用随机森林分类器来解决上述问题。因为不同公司的数据存在大量的特征和大的方差,随机森林模型对数据的拟合最好,提供了最好的整体精度。评价方法
评估数据的任务分4个步骤完成
数据清理
由于我们操作的数据来自不同来源的多个数据集,因此数据清理是确保这些数据集的数据表示一致所必需的一项主要操作。破产预测
申请破产的公司的数据集不包含非破产公司的财务特征数据,因此我们没有一个可以用来直接训练模型的数据集。为了解决这个问题,我们使用了来自纽约证券交易所上市公司的更大金融数据集的前几年的数据,并将其添加到这个数据集中,以确保该数据集符合通用规则。然后我们在这个数据集上训练了一个SVM,并验证其AUC得分约为0.75。时间序列分析
公司股票价格数据包含纽交所上市的约500家公司的每日收盘价。该数据被按比例缩小,以包含每周平均股价。由于时间序列对不同的公司会有不同的表现,因此有必要分别为每个公司建模。 不出所料,在某些情况下数据显示了强烈的趋势和季节性,必须通过数据集的差分来删除趋势和季节性,然后执行ARIMA模型。根据ACF和PACF绘图分析和手工试验,选择的p值和q值分别为2和1。在建模时,平均绝对误差为~0.05,这表明时间序列分析是相当准确的。用预测数据增强初始数据集
包含纽约证券交易所上市公司财务信息的数据集用预测破产价值和两年内各自股票价格变化百分比的复合标签进行了增强。这个标签是连续的,我们将它四舍五入到小数点后一位,然后乘以10得到一个整数。这个标签用于训练随机森林分类器,以确定模型认为对预测公司的增长趋势最重要的特征。对特征进行分析并找出特征与标签之间的相关关系。 随机森林分类器本身的分析是通过观察产生的混淆矩阵来评估的。由于标签是多类的,而不是二分类的,因此不能绘制ROC曲线来评价模型结果。然而马修斯相关系数却可以很好地衡量置信度。假设 / 限制
1、破产预测是机器学习研究的一个重要课题。关于这个话题有几篇研究论文,其中几篇使用了神经网络和先进的机器学习技术来更加精确可靠地预测破产的可能性。我们发现一些属性在这些模型中被普遍使用,因此并假设这些属性与公司破产的概率高度相关。 当然,如此决策另一个重要原因是,因为本次项目无法获得包含更多破产公司财务数据的公共数据集。因此,我们只使用这些相关度最高的特征来训练预测器,这是一个极其简单的破产预测模型。 2、发现 ACF 和 PACF 图非常模糊,并且不足以帮助确定 AR 和 MA 参数值。因此,我们尝试了一些值,并假设 (2,1) 组合最能预测数据。 3、增强步骤包括合并二进制预测破产值和连续平均时间序列预测。我们假设这是一个很好的指标,可以判断公司是上升还是下降,因此,向公司提供贷款是否安全。类范围问题
使用多种分类策略并对时间序列进行建模后,可以通过增加特征和数据点的数量来进一步进行这种分析,以实现更好的破产预测,以及调整时间序列模型的 AR 和 MA 参数。 鉴于当前的分析,我们发现了与目标变量相关的多个特征,这种分析有助于补充组织的传统启发式知识。银行和其他金融贷款机构的信息存储可以使用这种分析来更多地关注这些特征,这是通过代表性或推论分析可能无法实现的。 原始提案的变化及其原因:我们最初的提议包含一个策略,即只使用破产预测器来为金融数据集提供标签。然而,经过仔细分析,我们发现它不能作为公司整体地位的一个足够全面的指标。因此,我们决定通过对公司股票趋势的时间序列分析来增强它,这将是组织增长/下降的更好指标。代码
导入相关模块
import numpy as np
import pandas as pd
import re
import warnings
from matplotlib import pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn import preprocessing as pp
from sklearn import svm
from sklearn.ensemble import RandomForestClassifier
from sklearn import metrics
from statsmodels.stats.stattools import durbin_watson
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from statsmodels.tsa import arima_model
from statsmodels.graphics.api import qqplot
warnings.filterwarnings('ignore')
数据预处理
定义了几个函数,这里包括数据清洗、时间解析、稳定性检测。
def cleanColumnName(column):
#删除列名中的符号
column = re.sub('W+',' ', column.strip())
#删除列名末尾的所有空格
column = column.strip()
# 用'_'替换单词之间的空格
return column.lower().replace(" ","_")
def dateParse(dates):
return pd.datetime.strptime(dates, '%Y-%m-%d')
def test_stationarity(ticker, timeseries):
# 确定滑动窗口统计
rolmean = timeseries.rolling(window=7, center=False).mean()
rolstd = timeseries.rolling(window=7, center=False).std()
#绘制滑动窗口统计图:
orig = plt.plot(timeseries, color='blue',label='Original')
mean = plt.plot(rolmean, color='red', label='Rolling Mean')
std = plt.plot(rolstd, color='black', label = 'Rolling Std')
plt.legend(loc='best')
plt.title(ticker)
plt.show(block=False)
# 自相关的durbin_watson统计
dftest = durbin_watson(timeseries)
print(ticker)
print("Durbin-Watson statistic for "+ticker+": ",dftest)
数据清洗
从数据集中删除不必要的列。这完全是启发式的,因为我们完全根据自己对这些列的意义的理解来删除它们。
# 读取数据
bankrupt_companies = pd.read_csv("public_company_bankruptcy_cases.csv")
companies_stock_prices = pd.read_csv("prices-split-adjusted.csv",
parse_dates=True,
usecols=["date","symbol","close"],
date_parser=dateParse)
nyse_data = pd.read_csv("fundamentals.csv", index_col='Unnamed: 0')
bankrupt_companies.drop(["DISTRICT", "STATE", "COMPANY NAME"],
axis=1, inplace=True)
nyse_data.drop(["Deferred Asset Charges","Deferred Liability Charges",
"Depreciation","Earnings Before Tax","Effect of Exchange Rate",
"Equity Earnings/Loss Unconsolidated Subsidiary","Goodwill",
"Income Tax","Intangible Assets","Interest Expense","Liabilities",
"Minority Interest","Misc. Stocks","Net Cash Flow-Operating",
"Net Cash Flows-Financing","Net Cash Flows-Investing",
"Net Income Adjustments","Net Income Applicable to Common Shareholders",
"Net Income-Cont. Operations","Operating Income","Operating Margin",
"Other Assets","Other Current Assets","Other Current Liabilities",
"Other Financing Activities","Other Investing Activities",
"Other Liabilities","Other Operating Activities","Other Operating Items",
"Pre-Tax Margin","Pre-Tax ROE","Research and Development",
"Total Current Assets","Total Current Liabilities",
"Total Liabilities & Equity","Treasury Stock", "For Year"],
axis=1, inplace=True)
# 数据清理,使列名格式一致
bankrupt_companies.columns = map(cleanColumnName, bankrupt_companies.columns)
bankrupt_companies.columns = ["total_assets", "total_liabilities"]
companies_stock_prices.columns = map(cleanColumnName, companies_stock_prices.columns)
nyse_data.columns = map(cleanColumnName, nyse_data.columns)
nyse_data.head()

缺失值处理
从各自的数据集中删除NaN值。
bankrupt_companies.dropna(axis=0, subset=['total_assets', 'total_liabilities'],
inplace=True)
nyse_data.dropna(axis=1, how='any', inplace=True)
nyse_data.dropna(axis=0, how='any', inplace=True)
companies_stock_prices.dropna(axis=0, how='any', inplace=True)
训练SVM作为破产预测器
创建包含2013年未破产公司数据的新dataframe。
nyse_2013 = nyse_data.loc[nyse_data['period_ending'].str.contains("2013"),
["total_assets", "total_liabilities"]]
nyse_2013 = nyse_2013.sample(
n=bankrupt_companies.shape[0],
replace=False)
随机抽样该数据集,以获得一个数据帧,其中包含与其他数据集中破产公司数量相同的非破产公司的数据。
nyse_2013.set_index([[x for x in range(bankrupt_companies.index[-1]+1,
bankrupt_companies.index[-1]+nyse_2013.shape[0]+1)]],
inplace=True)
手动将列“bankrupt”添加到要用作标签的数据集。
bankrupt_companies["stability"] = 0
nyse_2013["stability"] = 1
合并破产数据和非破产数据,生成一个可用于训练分类器的数据。
merged_bankruptcy_dataset = pd.concat(
[bankrupt_companies, nyse_2013])
# 缩放数据以确保资产和负债在相同的范围内
scaler = pp.MinMaxScaler()
scaler.fit(merged_bankruptcy_dataset[["total_assets", "total_liabilities"]])
merged_bankruptcy_dataset[["total_assets", "total_liabilities"]] = scaler.transform(merged_bankruptcy_dataset[["total_assets", "total_liabilities"]])
将合并的数据集随机分割为训练数据集和测试数据集,用于训练决策树。
train_bankruptcy_data, test_bankruptcy_data,
train_bankruptcy_target, test_bankruptcy_target = train_test_split(
merged_bankruptcy_dataset.iloc[:,0:-1],
merged_bankruptcy_dataset.iloc[:,-1],
test_size=0.25 )
在训练数据上训练支持向量机。
Svm_model = svm.LinearSVC()
Svm_model.fit(train_bankruptcy_data, train_bankruptcy_target)
print(train_bankruptcy_data.shape,
Svm_model.score(train_bankruptcy_data, train_bankruptcy_target))
print(test_bankruptcy_data.shape,
Svm_model.score(test_bankruptcy_data, test_bankruptcy_target))
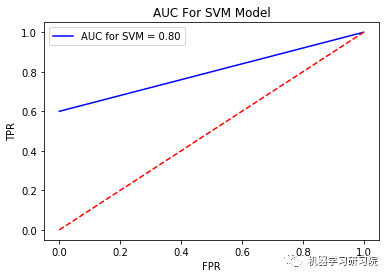
((190, 2), 0.83157894736842108) ((64, 2), 0.8125) 计算和绘制ROC和面积下曲线,以了解分类器的准确性
FPR, TPR, _ = metrics.roc_curve(test_bankruptcy_target, Svm_model.predict(test_bankruptcy_data))
auc = metrics.auc(FPR, TPR)
plt.plot(FPR, TPR, 'b', label = 'AUC for SVM = %0.2f' %auc)
plt.title("AUC For SVM Model")
plt.legend(loc='best')
plt.plot([0,1], [0,1], 'r--')
plt.xlabel('FPR')
plt.ylabel('TPR')
plt.show()
 只保留所有公司去年的数据。我们将只考虑最新的数据,并在原始数据集中添加破产的预测值。
只保留所有公司去年的数据。我们将只考虑最新的数据,并在原始数据集中添加破产的预测值。
nyse_data.drop_duplicates(subset='ticker_symbol', keep='last', inplace=True)
nyse_data["stability"] = Svm_model.predict(scaler.transform(nyse_data[["total_assets",
"total_liabilities"]]))
print("Companies predicted to go bankrupt over a 4 year period: ",
len(nyse_data.loc[nyse_data["stability"] != 1, "ticker_symbol"]))
Companies predicted to go bankrupt over a 4 year period: 114
时间序列分析
companies_stock_prices["date"] = pd.to_datetime(companies_stock_prices["date"],
format="%Y-%m-%d")
companies_stock_prices.dropna(axis=0,
how='any',
inplace=True)
# 按股票代码排序
companies_stock_prices.sort_values(by=["symbol", "date"], inplace=True)
假设每个公司的股票趋势是不同的,我们需要为每个公司建模不同的时间序列,方法是将每个公司的数据以单独的键存储在字典中。字典存储每个公司的每周股票价格,将每个公司的数据添加到字典中的单独键中,这样就可以对每个公司分别进行时间序列分析。
weekly_stock_prices = {}
for i in np.unique(companies_stock_prices["symbol"].values):
weekly_stock_prices[i] = companies_stock_prices.loc[
companies_stock_prices["symbol"] == i, :].copy()
weekly_stock_prices[i] = weekly_stock_prices[i].reset_index(drop=True)
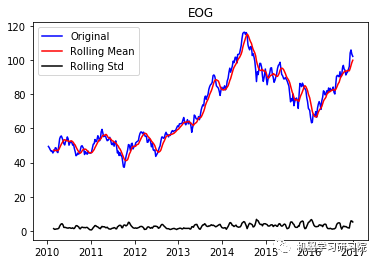
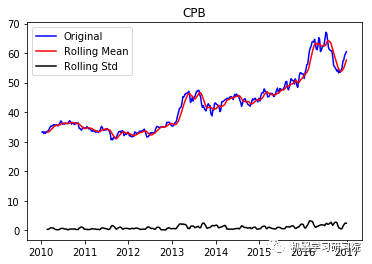
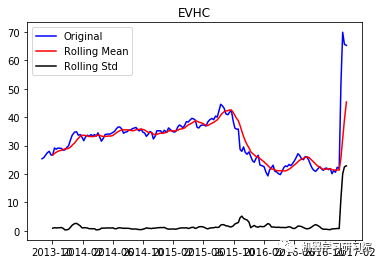
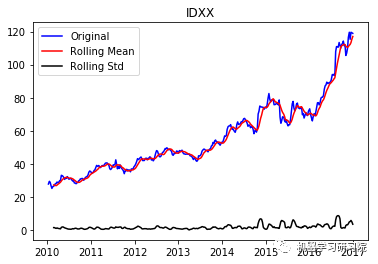
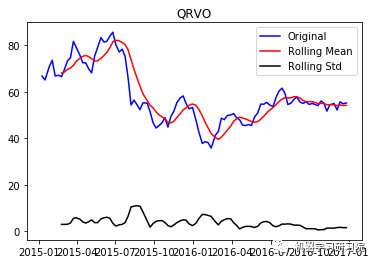
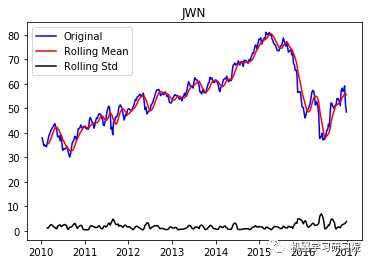
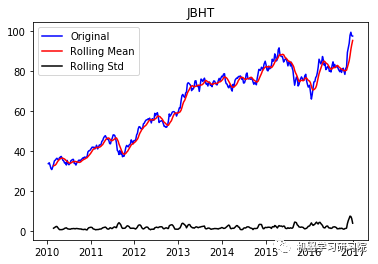
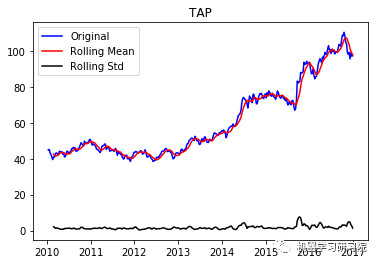
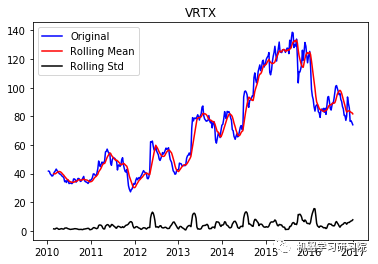
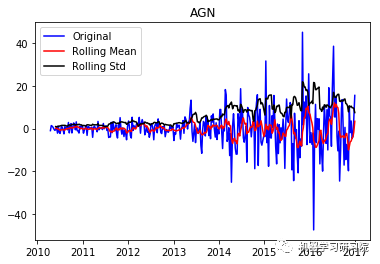
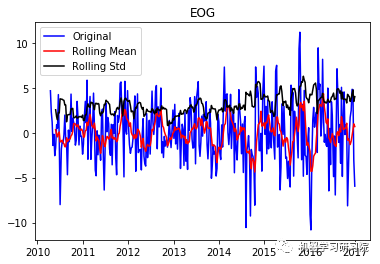
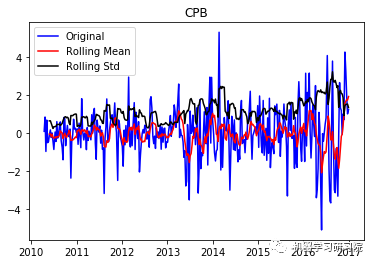
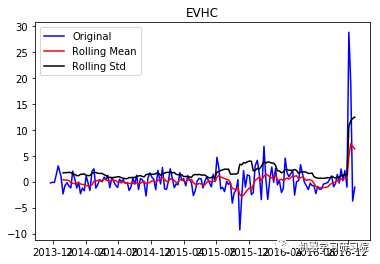
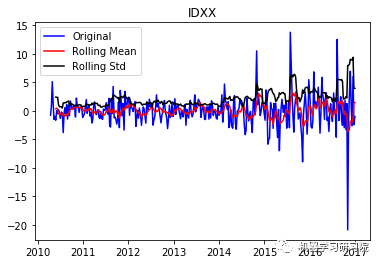
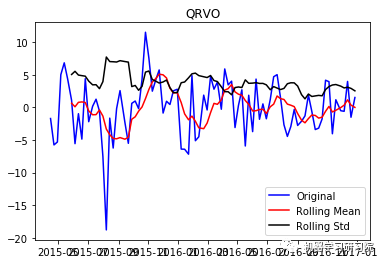
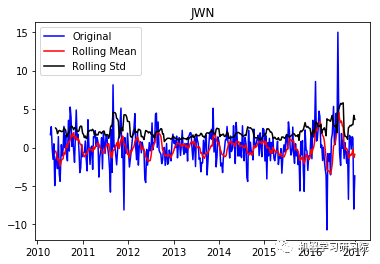
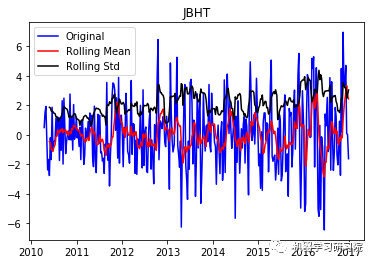
通过每周只保留一天的数据,将每日库存数据转换为每周。因为大约有450家公司,所以只显示前10个地块,而且绘制所有地块需要大量时间。趋势和季节性可以假定存在于所有这些。
count = 0
for i in weekly_stock_prices:
weekly_mean = weekly_stock_prices[i]["close"].rolling(window=5, center=False).mean()[4:]
# 通过每周只保留一天的数据,将每日库存数据转换为每周
weekly_stock_prices[i] = weekly_stock_prices[i].loc[weekly_stock_prices[i].index % 5 == 0, :]
weekly_stock_prices[i]["close"] = weekly_mean
weekly_stock_prices[i].index = weekly_stock_prices[i]["date"]
weekly_stock_prices[i].drop(["symbol", "date"], axis=1, inplace=True)
weekly_stock_prices[i].dropna(axis=0, how='any', inplace=True)
count += 1
if count <= 10:
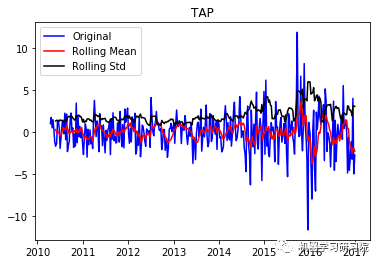
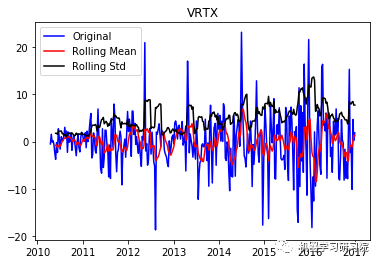
test_stationarity(i, weekly_stock_prices[i])

AGN ('Durbin-Watson statistic for AGN: ', array([ 0.00106633]))

EOG ('Durbin-Watson statistic for EOG: ', array([ 0.00104565]))

CPB ('Durbin-Watson statistic for CPB: ', array([ 0.00042048]))

EVHC ('Durbin-Watson statistic for EVHC: ', array([ 0.00806171]))

IDXX ('Durbin-Watson statistic for IDXX: ', array([ 0.00094586]))

QRVO ('Durbin-Watson statistic for QRVO: ', array([ 0.00290384]))

JWN ('Durbin-Watson statistic for JWN: ', array([ 0.00088175]))

JBHT ('Durbin-Watson statistic for JBHT: ', array([ 0.00059562]))

TAP ('Durbin-Watson statistic for TAP: ', array([ 0.00062282]))

VRTX ('Durbin-Watson statistic for VRTX: ', array([ 0.00270465])) 正如可以预期的那样,股票价格数据显示了一个很容易看到的趋势,而且在许多情况下,更仔细的检查也会显示出季节性的存在。低的Durbin-Watson统计值是高正自相关的证据,这也是可以理解的,因为股票价格依赖于以前的值。因此,要对该数据进行ARIMA分析,首先需要对其进行操作,以得到一个平稳的数据。
# 对数据进行平稳处理
count = 0
weekly_stock_prices_log = {}
for i in weekly_stock_prices:
# 对数据进行差分来去除数据中的趋势和季节性
weekly_stock_prices_log[i] = weekly_stock_prices[i].copy()
weekly_stock_prices_log[i]["first_difference"] = weekly_stock_prices_log[i]["close"] - weekly_stock_prices_log[i]["close"].shift(1)
weekly_stock_prices_log[i]["seasonal_first_difference"] = weekly_stock_prices_log[i]["first_difference"] - weekly_stock_prices_log[i]["first_difference"].shift(12)
count += 1
if count <=10:
test_stationarity(i, weekly_stock_prices_log[i]["seasonal_first_difference"].dropna(inplace=False))

AGN ('Durbin-Watson statistic for AGN: ', 1.8408166958817405)

EOG ('Durbin-Watson statistic for EOG: ', 1.6299518594407623)

CPB ('Durbin-Watson statistic for CPB: ', 1.5454599084578173)

EVHC ('Durbin-Watson statistic for EVHC: ', 1.4213426917002945)

IDXX ('Durbin-Watson statistic for IDXX: ', 1.7448077126902013)

QRVO ('Durbin-Watson statistic for QRVO: ', 1.3805906045088099)

JWN ('Durbin-Watson statistic for JWN: ', 1.6385737145457053)

JBHT ('Durbin-Watson statistic for JBHT: ', 1.6966894515415203)

TAP ('Durbin-Watson statistic for TAP: ', 1.8412354264794373)

VRTX ('Durbin-Watson statistic for VRTX: ', 1.6067817382582221) 现在从结果可以看出,这已经失去了先前所具有的趋势和季节性。Durbin-Watson统计量也显示了一个值~2,因此我们可以得出残差是平稳的,可以继续对其进行分析操作。
# 通过绘制ACF和PACF图来确定自回归和移动平均参数。
count = 0
for i in weekly_stock_prices_log:
fig = plt.figure(figsize=(12,5))
ax1 = fig.add_subplot(121)
plot_acf(weekly_stock_prices_log[i]["seasonal_first_difference"].iloc[13:],
lags=50, title="Autocorrelation for "+i, ax=ax1)
ax2 = fig.add_subplot(122)
plot_pacf(weekly_stock_prices_log[i]["seasonal_first_difference"].iloc[13:],
lags=50, title="Partial Autocorrelation for "+i, ax=ax2)
count += 1
if count == 5:
break
plt.show()




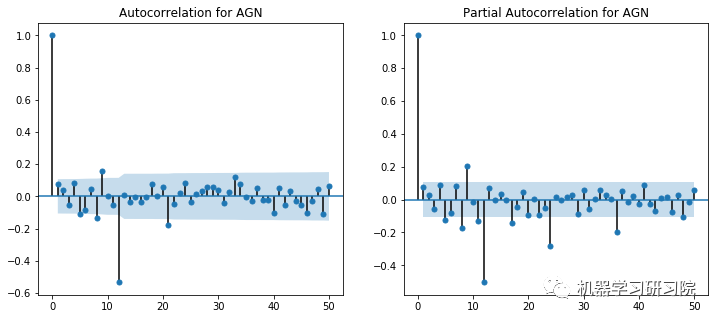
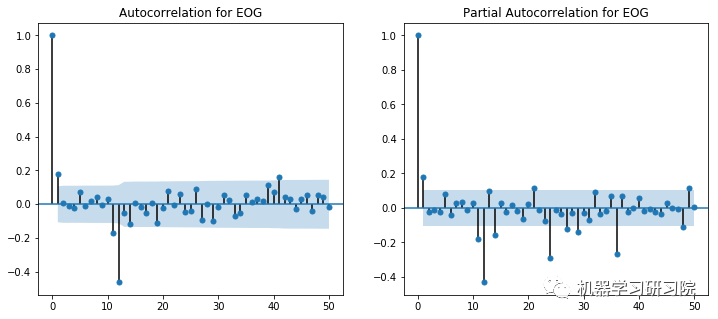
 ACF和PACF图显示在滞后1时出现峰值。然而,这些图本身并不是决定性的,因为没有一个可以说是指数下降的,当然,也显示了一些异常值。使用不同p和q值的试验在(2,1)处显示出显著更好的结果。
对所有公司进行ACF-PACF分析是不可能的,因此对于SVD不收敛于(2,1)的实例,使用了(1,0)的回退值。
ACF和PACF图显示在滞后1时出现峰值。然而,这些图本身并不是决定性的,因为没有一个可以说是指数下降的,当然,也显示了一些异常值。使用不同p和q值的试验在(2,1)处显示出显著更好的结果。
对所有公司进行ACF-PACF分析是不可能的,因此对于SVD不收敛于(2,1)的实例,使用了(1,0)的回退值。
count = 0
stock_predictions = {}
for i in weekly_stock_prices_log:
# 将可用数据分割为训练,使用剩余的数据点进行准确性检查
split_point = len(weekly_stock_prices_log[i]) - 20
# 从数据集的最后日期到2018-12-31的周数加117
num_of_predictions = len(weekly_stock_prices_log[i]) + 117
training = weekly_stock_prices_log[i][0:split_point]
model = {}
# 首先尝试使用p=2, q=1建模,如果失败,使用p=1, q=0
try:
model = arima_model.ARMA(training["close"], order=(2,1)).fit()
except:
model = arima_model.ARMA(training["close"], order=(1,0)).fit()
# 在dataframe中添加预测值,以便于进一步的操作。
daterange = pd.date_range(training.index[0], periods=num_of_predictions, freq = 'W-MON').tolist()
stock_predictions[i] = pd.DataFrame(columns=["date", "prediction"])
stock_predictions[i]["date"] = daterange
stock_predictions[i]["prediction"] = model.predict(start=0, end=num_of_predictions)
stock_predictions[i].set_index("date", inplace=True)
# 绘制QQPlot来检查残差是否均匀分布
if count < 5:
resid = model.resid
print("For "+i+": ",stats.normaltest(resid))
qqplot(resid, line='q', fit=True)
plt.show()
count += 1
('For AGN: ', NormaltestResult(statistic=472.93123930305205, pvalue=2.0150518495630914e-103))

('For EOG: ', NormaltestResult(statistic=120.49648362661878, pvalue=6.8315780758386102e-27))

('For CPB: ', NormaltestResult(statistic=339.86796767404019, pvalue=1.579823361925116e-74))

('For EVHC: ', NormaltestResult(statistic=69.17501926644907, pvalue=9.5243516902465695e-16))

('For IDXX: ', NormaltestResult(statistic=360.2101109972532, pvalue=6.0446092870173276e-79))
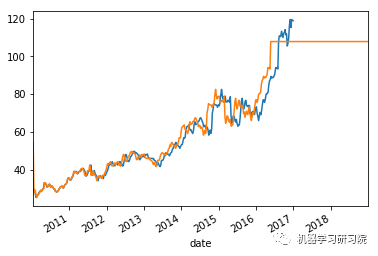
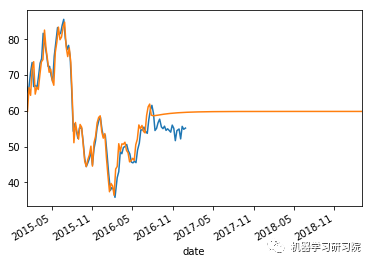
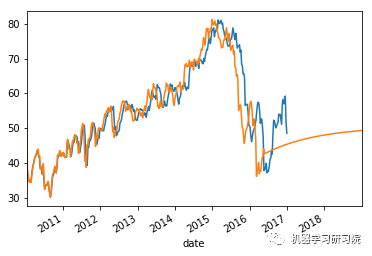
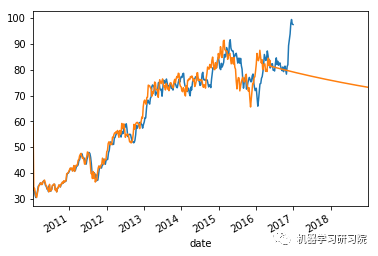
 上面这些图显示了合理的平等分布,因此我们可以得出结论,残差分析是适当的。
时间序列模型分析。
上面这些图显示了合理的平等分布,因此我们可以得出结论,残差分析是适当的。
时间序列模型分析。
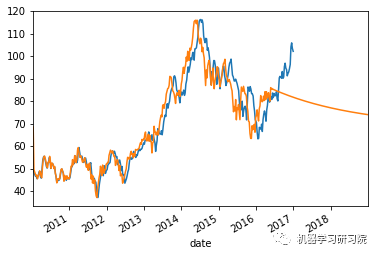
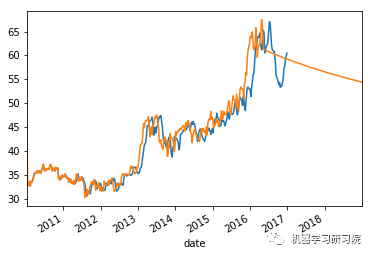
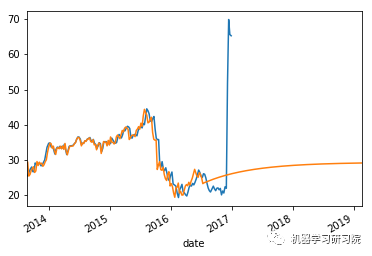
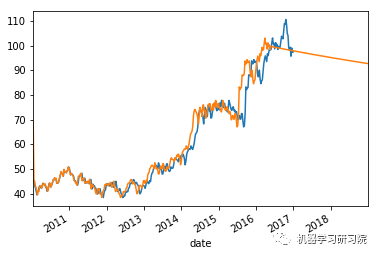
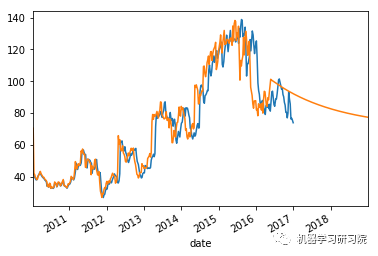
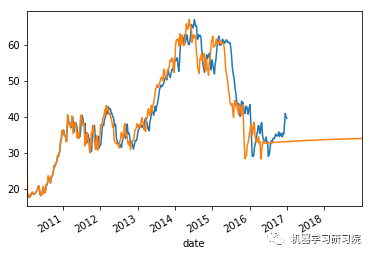
count = 0
for i in weekly_stock_prices_log:
# 将实际值与预测值进行对比
weekly_stock_prices_log[i]["close"].plot()
stock_predictions[i]["prediction"].plot()
plt.show()
# 计算验证数据点的平均绝对误差和平均预测误差
split_point = len(weekly_stock_prices_log[i]) - 20
forecastedValues = stock_predictions[i]["prediction"].iloc[split_point : len(weekly_stock_prices_log[i])]
actualValues = weekly_stock_prices_log[i]["close"].iloc[split_point:]
mfe = actualValues.subtract(forecastedValues).mean()
mae = (abs(mfe)/forecastedValues).mean()
display("Mean Absolute Error for "+i+": "+str(mae))
display("Mean Forecast Error for "+i+": "+str(mfe))
print "-----"*50
count += 1
if count > 10:
break

'Mean Absolute Error for AGN: 0.00193187347291' 'Mean Forecast Error for AGN: 0.481341889454' -------------------------------------------------

'Mean Absolute Error for EOG: 0.0798100720231' 'Mean Forecast Error for EOG: 6.73902186871' -------------------------------------------------

'Mean Absolute Error for CPB: 0.00893546704868' 'Mean Forecast Error for CPB: 0.54092487694' -------------------------------------------------

'Mean Absolute Error for EVHC: 0.143090575838' 'Mean Forecast Error for EVHC: -3.51053172619' -------------------------------------------------

'Mean Absolute Error for IDXX: 0.0264690184111' 'Mean Forecast Error for IDXX: 2.85600695121' -------------------------------------------------

'Mean Absolute Error for QRVO: 0.100785079934' 'Mean Forecast Error for QRVO: -5.95620693487' -------------------------------------------------

'Mean Absolute Error for JWN: 0.158397127455' 'Mean Forecast Error for JWN: 6.89272442754' -------------------------------------------------

'Mean Absolute Error for JBHT: 0.0206382415512''Mean Forecast Error for JBHT: 1.66385893237'-------------------------------------------------

'Mean Absolute Error for TAP: 0.0115749676383' 'Mean Forecast Error for TAP: 1.14684278635' -------------------------------------------------

'Mean Absolute Error for VRTX: 0.0246045992625' 'Mean Forecast Error for VRTX: 2.4170609498' -------------------------------------------------

'Mean Absolute Error for BWA: 0.0334229670671' 'Mean Forecast Error for BWA: 1.09813003018' ------------------------------------------------- 平均绝对误差值约等于0表明时间序列模型具有良好的预测精度。
使用预测数据增强初始数据集
创建新的列来存储预测的股票价格,计算一个百分比度量来估计公司股票的上涨或下跌,进而估计组织的增长,以便在所有组织中保持一个公平的范围。
nyse_data["stock_pred"] = np.nan
for i in stock_predictions:
perc=(stock_predictions[i]["prediction"].tail(105).mean() - stock_predictions[i]["prediction"].tail(105)[0])/stock_predictions[i]["prediction"].tail(105)[0]
nyse_data.loc[nyse_data["ticker_symbol"] == i, "stock_pred"] = perc
将预计的破产价值加到预计的股价中,生成一个能有效代表公司成长或衰退的复合标签。从数据集中删除不必要的和非数字列,以方便建模。
nyse_data["stock_pred"] += nyse_data["stability"]
nyse_data.drop(["period_ending", "stability", "ticker_symbol"], axis=1, inplace=True)
nyse_data.dropna(axis=0, subset=["stock_pred"], inplace=True)
缩放数据集的特性。
nyse_data_scaled = nyse_data.iloc[:,0:-1]
scaler = pp.StandardScaler()
nyse_data_scaled[nyse_data_scaled.columns] = scaler.fit_transform(nyse_data_scaled[nyse_data_scaled.columns])
将目标变量缩放到值-1和1之间,四舍五入到最近的第十位,并乘以10,以生成一个非连续的多值标签。
scaler = pp.MinMaxScaler(feature_range=(-1,1))
nyse_data_target_scaled = scaler.fit_transform(nyse_data.iloc[:,-1].reshape(-1,1)).round(decimals=1) * 10
将增强数据集分割为训练集和测试集,用于训练分类器。
train_data, test_data, train_target, test_target = train_test_split(nyse_data_scaled, nyse_data_target_scaled, test_size=0.25)
训练随机森林分类器。
RF = RandomForestClassifier()
RF.fit(train_data, train_target)
model_predictions = RF.predict(test_data)
print("Training:-->",train_data.shape, RF.score(train_data, train_target))
print("Testing:-->",test_data.shape, RF.score(test_data, test_target))
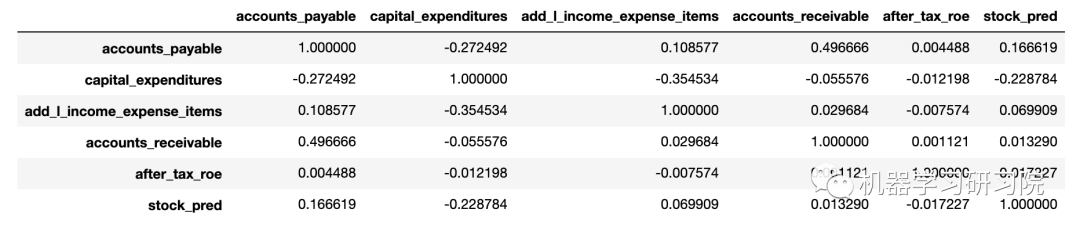
('Training:-->', (334, 34), 0.98502994011976053) ('Testing:-->', (112, 34), 0.7410714285714286) 分析随机森林模型发现的特征,使其与增强标签高度相关。观察数值相关性。
top_features = np.argsort(RF.feature_importances_[-5:])
top_features = np.append(top_features, -1)
display(nyse_data.iloc[:, top_features].corr())
 生成一个混淆矩阵并计算Matthews相关系数作为训练的随机森林分类器的评估指标。
生成一个混淆矩阵并计算Matthews相关系数作为训练的随机森林分类器的评估指标。
display("CONFUSION MATRIX: ",metrics.confusion_matrix(test_target, model_predictions))
display("MATTHEWS CORRELATION CO-EFFICIENT", metrics.matthews_corrcoef(test_target, model_predictions))
'CONFUSION MATRIX: ' array([[ 1, 4, 0, 0, 0, 0, 0, 0, 0], [ 2, 17, 0, 0, 0, 0, 0, 0, 0], [ 1, 1, 0, 0, 0, 0, 0, 0, 0], [ 0, 1, 0, 0, 0, 0, 0, 0, 0], [ 0, 0, 0, 0, 0, 4, 0, 0, 0], [ 0, 0, 0, 0, 0, 64, 3, 0, 0], [ 0, 1, 0, 0, 0, 7, 1, 0, 0], [ 0, 0, 0, 0, 0, 3, 1, 0, 0], [ 0, 0, 0, 0, 0, 0, 1, 0, 0]]) 'MATTHEWS CORRELATION CO-EFFICIENT' 0.53348354519442676
审核编辑 :李倩
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
【「时间序列与机器学习」阅读体验】全书概览与时间序列概述2024-08-07 2704
-
深度学习中的时间序列分类方法2024-07-09 2749
-
名单公布!【书籍评测活动NO.35】如何用「时间序列与机器学习」解锁未来?2024-06-25 2352
-
基于温度数据集的时间序列预测实战2022-10-24 2272
-
介绍有关时间序列预测和时间序列分类2021-07-12 1516
-
时间序列的特征表示和相似性度量研究分析2021-04-02 1056
-
《数据分析与挖掘实战》总结及代码---chap3数据探索2020-05-25 1422
-
基于密度感知模式的生物序列分类算法2018-03-29 966
-
基于关联矩阵的高效DNA序列挖掘算法2017-12-11 780
-
基于SAX的时间序列分类2017-11-30 1227
-
流式时间序列的实时相似度研究2017-11-20 718
-
基于时间序列数据挖掘的故障检测方法_李海林2017-01-08 746
-
DNA序列的分类模型2009-09-16 1029
-
基于符号化表示的时间序列频繁子序列挖掘2009-04-22 719
全部0条评论

快来发表一下你的评论吧 !

