

AEB精度指标中概率分布的取值计算方法
描述
导语:
SASETECH,Safety and Security Technology,是国内首个由汽车功能安全、信息安全专家发起组建的技术社区,致力于为汽车安全的从业者提供交流、学习、合作的中立性平台。安全是汽车的基石,安全从业者是人们生命及财产的守护者。我们希望SASETECH 打破高大上的壁垒,让更多工程师参与讨论、共同成长;让安全成为一个话题,是一个让大家讨论和思考的技术方向;让安全成为一种文化,是一个让企业和监管机构愈发重视的领域;建立安全的生态,让企业/从业者都能够有所收获、有所思考。
SOTIF中的定量分析(一)
前言
在上一篇中,我们以误制动为例做了SOTIF的定量分析,根据误制动的风险场景以及AEB算法,计算得到了对感知系统相对距离和相对速度的精度指标要求的函数,并取了一组数据:距离精度要求29.2%,速度精度要求20%。
但是这个精度指标是不完整的,因为感知一定会有误差,谁都不能保证传感器能百分之百达到这个要求。所以在定义精度时,会有一个与之相对应的概率值,通常假设误差满足正态分布,概率值一般取 2 sigma或3 sigma。其含义是感知输出误差分布在精度指标范围内的概率为95.4%(2 sigma)或99.7%(3 sigma)。
本篇文章将继续以AEB误制动为例,探讨这个概率的取值方法。
总体思路
首先,AEB有一个指标叫误报率,即在单位时间内误制动发生的概率,单位是h^-1。在ISO21448附录B中有关于AEB误报率指标计算的示例,其总体思想是要保证AEB系统误制动导致追尾的概率要小于人开车发生追尾的概率,即机器至少要比人开的好,这不是这篇文章讨论的重点,只要明白误报率的指标是可以知道的。
那么在多大的概率内满足精度指标才能满足整车AEB误报率的要求呢?有两个思路。
思路一是将误报率指标分解到各个参数(自上而下)。思路二是先给定一个概率(比如2 sigma),计算这个概率会导致的误报率(自下而上),看是否满足误报率目标。这里我们用第二种思路。
如果一个参数可以保证2 sigma满足精度指标,就意味着每一帧信号都会有95.4%的概率在精度阈值内,4.6%的概率超过阈值。我们可把超过阈值的信号认为是“失效”,那么4.6%就理解为信号的失效率。但是直觉告诉我们,一帧信号的“失效”不一定会导致危害发生。我们需要知道信号怎样的“失效”会导致整车层级的危害,才能探究信号的失效率和AEB误报率的关系。
注:
笔者这里参考了ISO26262硬件部分的概念。失效率:指单位时间内元器件失效的概率。PMHF(Probabilistic Metric for random Hardware Failure):单位时间内发生单点故障或多点故障中多点都发生故障的概率。一个元器件失效不一定会导致危害,只有发生单点故障,或者多点故障中的“多点”都发生故障,才会导致危害。PMHF就是用来度量导致危害的硬件失效概率密度的指标。信号“失效率”与AEB误报率的关系,就可以类比成硬件元器件的失效率和PMHF的关系。
问题一
问:哪几种信号失效的组合会导致危害。
这涉及到在该场景下,误制动发生与几种信号相关。我们称与误制动风险相关的信号为安全相关信号。若误制动和一个以上参数相关,在一个信号周期内,多个安全相关信号同时失效的概率(P)为这几个信号的失效概率相乘。
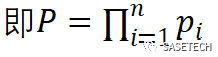
(1)
n为安全相关信号的个数;
为每个安全相关信号单帧的失效率。
问题二
问:上述失效信号的组合发几帧会导致危害。
此时需要定义危害,ISO21448附录B中对非预期制动的定义是非预期制动持续时间超过340ms。我认为这里的340ms是和制动系统的性能相关的,制动系统建压需要一定时间,而340ms就是制动建压达到某个减速度阈值的时间,这个减速度阈值就是危害发生的边界,或者S>0的边界。340ms是个参考值,制动系统建压速率越快,这个时间越小。
然后往前推导,制动系统建压340ms,需要AEB连续发送制动请求信号340ms。那么感知系统连续发几帧失效信号,才会导致AEB系统持续发340ms制动信号?
这里就需要知道AEB算法里的判断逻辑,比如判定制动的debounce次数,判定停止制动的debounce次数,接收感知信号的周期,算法运行周期等。结果为感知系统连续发N帧失效信号,会导致AEB发送超过340ms的制动请求信号,进而导致危害发生。
问题三
通过前两个问题,已经知道发生危害的条件是所有安全相关信号同时发生“失效”连续若干帧。那么第三个问题是:
车辆运行多长时间才会发生一次“连续N个信号周期发生n个安全相关信号都失效”的事件?
这个问题可以简化成一道概率题:已知某事件X发生的概率为P,那么使事件X连续发生N次所需尝试次数是多少?通过解答问题一和问题二,P和N都是已知的。
假设E(n)为事件X连续发生N次所需尝试次数的期望,那么E(N)和E(N-1)有如下关系:
E(N)=E(N-1)+1+P*0+(1-P)*E(N);
经过转换可得到公式:
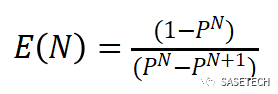
(2)
将P和N代入,即可求解尝试次数的期望。次数乘以信号周期就可以简单转换成时间、时间取倒数就是误报率。
可得误报率公式:
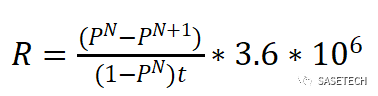
(3)
R为误报率,单位h^-1;t为信号周期,单位ms。
注:公式(2)解释和推导:连续发生N次的前提是先连续发生N-1次,然后再发生一次。但是发生N-1次之后的这次尝试有两种可能,一是事件X发生了,则不需再次尝试(对应公式中P*0),二是事件X未发生,则需要从头开始再尝试E(N)次(对应公式中(1-P)*E(N))。
可整理得到:E(N)=(E(N-1)+1)/P;
已知E(1)=1/P;E(2)=(1+P)/P^2;
E(N)=(1+P+P^2+…+P^N-1)/P^N
分子为等比数列求和,可化简得:
E(N)=(1-P^N)/(P^N-P^N+1)
计算结果
以车辆在直道中的发生误制动这个场景为例。已知风险场景与相对距离和相对速度两个参数相关,相对距离和相对速度精度指标的概率都取2 sigma。那么,P=4.6%*4.6%=0.21%。
假设导致危害需要的连续帧数N=5,信号发送周期t=10ms。
得:E=2.45*10^13;R=(1.47*10^-8)h^-1。
即每发送2.45*10^13帧信号,会出现一次连续5帧距离速度两个信号都失效的事件。转换成时间就是6.82*10^7小时发生一次;误报率1.47*10^-8。拿这个值与误报率指标比较大小,若不能满足则提高精度要求(精度值或概率值)。
下面给出几组计算结果供参考。
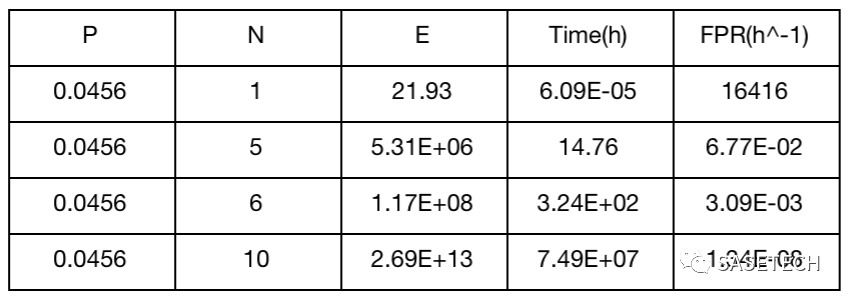
表1:一个安全相关信号(2 sigma)
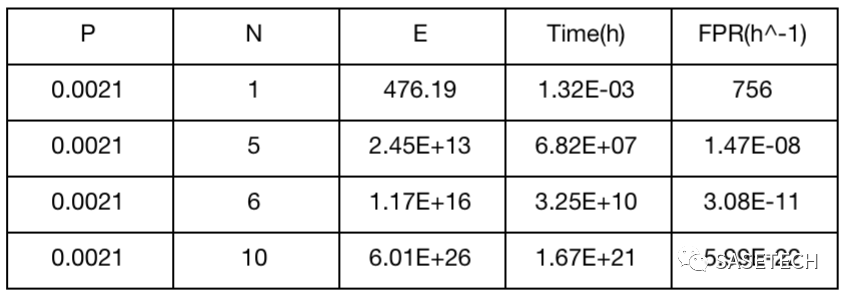
表2:两个安全相关信号(2 sigma)
由上表可见,与危害相关的信号越多,误报率越低。导致危害所需的信号连续失效次数越多,误报率越低。而且都是呈指数降低。这也对AEB的算法优化提供了参考。
总结
本文以误制动为例,探讨了精度指标中概率分布的取值计算方法。首先确定了总体思路是分析信号的失效率如何满足整车级误报率指标;然后将问题抽象成一个概率问题并推出误报率的计算公式;最后列出了几组计算结果。不足之处请指正。
作者简介
田野
曾任功能安全工程师,参与高低速智驾系统功能安全开发,底盘零件功能安全开发,以及预期功能安全预研项目,熟悉功能安全和预期功能安全分析方法,现从事嵌入式软件开发工作。
原文标题:SOTIF的定量分析(二)
文章出处:【微信公众号:SAE International】欢迎添加关注!文章转载请注明出处。
审核编辑:汤梓红
-
EMC计算方法和EMC仿真(1) ——计算方法简介2023-12-05 2822
-
二进制数据及取值范围的计算方法2023-11-08 4702
-
压力传感器精度的计算方法2023-06-18 4150
-
求π型阻抗匹配计算方法2019-03-14 10427
-
风力发电并网系统概率潮流计算2018-03-19 945
-
概率静态电压稳定计算方法2018-01-18 1027
-
电力系统连锁故障解析模型及概率计算方法2018-01-14 1274
-
电阻取值及计算方法2013-07-03 5469
-
仪器精度rdg,dgt,fs的解释和误差计算方法2012-10-01 20681
-
LED驱动电路工程中的计算方法2012-02-21 3450
-
高频开关电源系统可靠性指标MTBF的计算方法2010-11-08 1041
-
电气设计中负荷计算方法选择与探讨2010-01-27 490
-
分布式紧耦合虚拟专用网可靠性计算方法2009-11-13 599
-
多传感器航迹融合的评价指标及计算方法2009-06-22 512
全部0条评论

快来发表一下你的评论吧 !

