详解功率分析仪的基础知识

功率分析仪知识科普：功率的定义（Power）

对于功率测量重要的是先看看能量。在一个简单的系统中包含电源和负载。可以从电源把电能传送到负载，该电能可以被吸收或者转换为其他种类的能量（光、热、动能、……）。这就是所谓的有功能量，除此之外可以存储和返回到电源的能量称为无功能量。

功率定义为单位时间内传送的电能。所以在定义时间内可以传送功率给负载。部分功率可能会返回到电源（无功功率），其他的不会（有功功率）。

电功率可以分成四部分：

瞬时功率：    这是在某个时间点的功率。它等于这个时间点上电压和电流的乘积。

一连串的瞬时功率值得到功率的波形。此功率的符号是“p(t)”。所以

公式是：

p(t)=u(t)*i(t)

公式9：瞬时功率的定义

视在功率：    视在功率是电压和电流真有效值的乘积。不考虑信号的相移和畸变。

公式是：

S=Utrms*Itrms

公式10：视在功率的定义

有功功率：有功功率是在单位时间内传送到负载且不返还的能量。所以有功功率是

 功率波形的平均值。公式是：

P=1Tt=0Tut*itdt

公式11：有功功率的定义

 P的正负号取决于功率的流向。有功功率仅由频率相同的电压和电流成

分产生。

无功功率：    无功功率是单位时间内传送到负载且返还的能量。计算公式：

Q=S2-P2

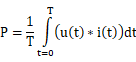
公式12：无功功率的定义

无功功率产生有两个原因：

1. 由相同频率的电压和电流成分之间的相位差引起“相移无功功率”（也称“位移无功功率”），符号Qshift，计算公式如下：

Qshift=i=1nUi*Ii*sinφ

公式13：相移无功功率的定义

相移无功功率仅由频率相同的电压和电流成分产生。

1. 不同频率的电压和电流成分之间产生的功率称为“畸变无功功率”，用D或者Qdist表示。

这两种无功功率的几何相加就是总的无功功率：

Q=Qshift2+Qdist2=Qshift2+D2

公式14：总无功功率的定义

可以使用上面的公式进行计算。

为了更好地理解，可见下图：

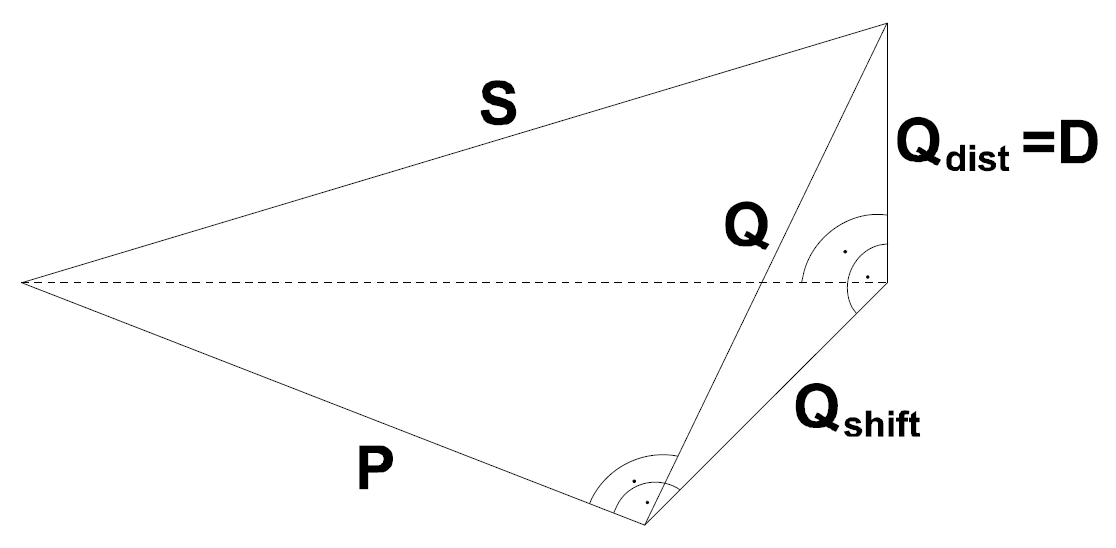
图1：不同功率之间的图形关系

系统的畸变无功功率可以用如下的公式计算：

D=S2-P2-Qshift2

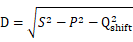
公式15：畸变无功功率的定义

两个简单的规则：

 规则一、相同频率的电压和电流仅能产生有功功率和相移无功功率。

可以用如下公式描述功率波形：

pt=i*sinωt+φi*u*sinωt+φu=i*u*(12cosφi-φu-12cos2ωt+φi+φu)

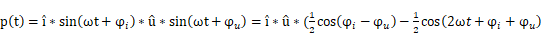
公式16：相同频率信号的功率波形

如前面所说（见公式11），有功功率是功率波形的平均值。当仔细观察上述公式你会发现只有

i*u*12cosφi-φu

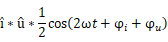
部分的平均值可能不为零！这取决于电压和电流信号的相角。剩下的部分

i*u*12cos2ωt+φi+φu

不会产生有功功率，因为它的一个信号周期内的平均值永远是0！

第一部分的公式可以修改成常见的公式：

 pt=i*u*12cosφi-φu

      =i2*u2*cosφi-φu

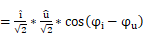
= I*U*cos(φ)

公式17：相同频率信号的有功功率

请注意该公式仅在电压和电流成分的频率相同时是正确的。

规则二、不同频率的成分将产生畸变无功功率

功率波形可以用如下公式描述：

        pt=i*sinω1t+φi*u*sinω2t+φu

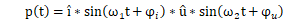
=i*u*(12cos(ω1-ω2)*t+φi-φu-12cos(ω1+ω2)*t+φi+φu)

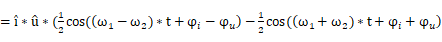
公式18：不同频率信号的功率波形

因此可以看到，第一部分和第二部分在一个整周期的平均值是零。所以都不会产生任何有功功率。此信号的最大周期时间可以按如下公式计算：

T=1gcd⁡(f1,f2)1

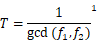
公式19：不同频率信号的功率波形周期时间

1: gcd是最大公约数。此函数仅对整数有效。如果不是，则分数必需乘以一个公因数。

如f1=50Hz, f2=50.2Hz, 则T=10/gcd(500,502)=5s

在上面的所有定义中，我们都说到了“定义的时间”。对于周期性信号这个时间是完整周期的整数倍（因为在一个完整的周期之后，信号是周期性的，不同测量的数值是相同的；如果测量的不是一个完整的周期，那么下一次测量的结果就完全不同了）。如果使用多个周期进行测量，那么将得到此测量时间内的平均值。因此，您可以在LMG仪器设置一个基本的“周期时间”。此周期时间确定了某些周期内的平均值。

非周期性信号如启动特性并不那么容易测量，因为很难确定“定义的时间”。例如，如果启动电梯，就会把能量传递到电机上，电机就是负载；然后电梯运行几分钟，然后停止；在电机停止的同时，一些能量回收到电源。这些能量是无功能量。如果以 1 秒的周期进行测量，在启动时测量传输到电机的以及在停止时从电机返回的有功能量，因为您的"定义时间"不够长，无法将关闭计入计算中。因此，在测量非周期性信号时，可能存在误差。

当然，你可以测量许多短序列的真有效值和有功功率值。这些值在“定义的时间”也即测量时间中是正确的。仅用户能确定是否有一些功率返回。功率测试仪LMG671。

审核编辑：汤梓红