关于贪心算法详解

 

顾名思义，贪心算法总是作出在当前看来最好的选择。也就是说贪心算法并不从整体最优考虑，它所作出的选择只是在某种意义上的局部最优选择。

 

当然，希望贪心算法得到的最终结果也是整体最优的。虽然贪心算法不能对所有问题都得到整体最优解，但对许多问题它能产生整体最优解。

 

如单源最短路经问题，最小生成树问题等。在一些情况下，即使贪心算法不能得到整体最优解，其最终结果却是最优解的很好近似。

 

基本思路：

 

1. 建立数学模型来描述问题。

⒉.把求解的问题分成若干个子问题。

⒊.对每一子问题求解，得到子问题的局部最优解。

⒋.把子问题的解局部最优解合成原来解问题的一个解。

 

实现该算法的过程：

 

⒈.从问题的某一初始解出发;

2. while 能朝给定总目标前进一步 do

3.求出可行解的一个解元素;

4.由所有解元素组合成问题的一个可行解。从问题的某一初始解出发

 

 

背包问题

 

有一个背包，最多能承载150斤的重量，现在有7个物品，重量分别为[35, 30, 60, 50, 40, 10, 25]，它们的价值分别为[10, 40, 30, 50, 35, 40, 30]，应该如何选择才能使得我们的背包背走最多价值的物品？

 

把物品一个个的往包里装，要求装入包中的物品总价值最大，要让总价值最大，就可以想到怎么放一个个的物品才能让总的价值最大，因此可以想到如下三种选择物品的方法，即可能的局部最优解：

 

1：每次都选择价值最高的往包里放。

2：每次都选择重量最小的往包里放。

3：每次都选择单位重量价值最高的往包里放。

4：选择价值最高的，按照制订的规则（价值）进行计算，顺序是：4 2 6 5 。

 

最终的总重量是：130；最终的总价值是：165。

 

2：选择重量最小的，按照制订的规则（重量）进行计算，顺序是：6 7 2 1 5 。

 

最终的总重量是：140；最终的总价值是：155。可以看到，重量优先是没有价值优先的策略更好。

 

3:选择单位密度价值最大的，按照制订的规则（单位密度）进行计算，顺序是：6 2 7 4 1。

 

最终的总重量是：150；最终的总价值是：170。

 

可以看到，单位密度这个策略比之前的价值策略和重量策略都要好。

 

 

单源最大路径问题

 

给定带权有向图G =(V,E)，其中每条边的权是非负实数。另外，还给定V中的一个顶点，称为源。现在要计算从源到所有其它各顶点的最短路长度。这里路的长度是指路上各边权之和。这个问题通常称为单源最短路径问题。

 

Dijkstra算法是解单源最短路径问题的贪心算法。

 

其基本思想是，设置顶点集合S并不断地作贪心选择来扩充这个集合。一个顶点属于集合S当且仅当从源到该顶点的最短路径长度已知。

 

初始时，S中仅含有源。设u是G的某一个顶点，把从源到u且中间只经过S中顶点的路称为从源到u的特殊路径，并用数组dist记录当前每个顶点所对应的最短特殊路径长度。

 

Dijkstra算法每次从V-S中取出具有最短特殊路长度的顶点u，将u添加到S中，同时对数组dist作必要的修改。一旦S包含了所有V中顶点，dist就记录了从源到所有其它顶点之间的最短路径长度。

 

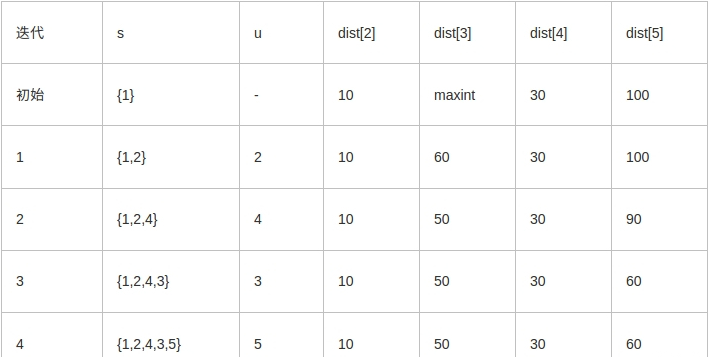
例如，对下图中的有向图，应用Dijkstra算法计算从源顶点1到其它顶点间最短路径的过程列在下表中。

 

 

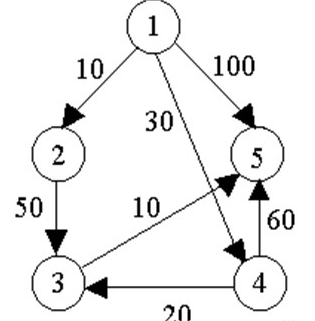
Dijkstra算法的迭代过程：

 

 

 

算法的正确性和计算复杂性

 

(1)贪心选择性质

 

(2)最优子结构性质

 

(3)计算复杂性

 

对于具有n个顶点和e条边的带权有向图，如果用带权邻接矩阵表示这个图，那么Dijkstra算法的主循环体需要O(n)时间。这个循环需要执行n-1次，所以完成循环需要O(n)时间。算法的其余部分所需要时间不超过O(n^2)。

 

代码实现(来自于第四个参考链接)：

 

•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  

#include #include #include using namespace std ;
class BBShortestDijkstra{public:    BBShortestDijkstra (const vector<vector<int> >& vnGraph)         :m_cnMaxInt (numeric_limits<int>::max())     {        m_vnGraph = vnGraph ;        m_stCount = vnGraph.size () ;        m_vnDist.resize (m_stCount) ;        for (size_t i = 0; i < m_stCount; ++ i) {            m_vnDist[i].resize (m_stCount) ;        }    }        void doDijkatra (){        int nMinIndex = 0 ;        int nMinValue = m_cnMaxInt ;        vector<bool> vbFlag (m_stCount, false) ;        for (size_t i = 0; i < m_stCount; ++ i) {            m_vnDist[0][i] = m_vnGraph[0][i] ;            if (nMinValue > m_vnGraph[0][i]) {                nMinValue = m_vnGraph[0][i] ;                nMinIndex = i ;            }        }
        vbFlag[0] = true ;        size_t k = 1 ;        while (k < m_stCount) {            vbFlag[nMinIndex] = true ;            for (size_t j = 0; j < m_stCount ; ++ j) {                // 没有被选择                if (!vbFlag[j] && m_vnGraph[nMinIndex][j] != m_cnMaxInt ) {                    if (m_vnGraph[nMinIndex][j] + nMinValue                        < m_vnDist[k-1][j]) {                        m_vnDist[k][j] = m_vnGraph[nMinIndex][j] + nMinValue ;                    }                    else {                        m_vnDist[k][j] = m_vnDist[k-1][j] ;                    }                }                else {                    m_vnDist[k][j] = m_vnDist[k-1][j] ;                }            }            nMinValue = m_cnMaxInt ;            for (size_t j = 0; j < m_stCount; ++ j) {                if (!vbFlag[j] && (nMinValue > m_vnDist[k][j])) {                    nMinValue = m_vnDist[k][j] ;                    nMinIndex = j ;                }            }            ++ k ;        }
        for (int i = 0; i < m_stCount; ++ i) {            for (int j = 0; j < m_stCount; ++ j) {                if (m_vnDist[i][j] == m_cnMaxInt) {                    cout << "maxint " ;                }                else {                    cout << m_vnDist[i][j] << " " ;                }            }            cout << endl ;        }    }private:      vector<vector<int> >    m_vnGraph ;    vector<vector<int> >    m_vnDist ;    size_t m_stCount ;    const int m_cnMaxInt ;} ;
int main(){    const int cnCount = 5 ;    vector<vector<int> > vnGraph (cnCount) ;    for (int i = 0; i < cnCount; ++ i) {        vnGraph[i].resize (cnCount, numeric_limits<int>::max()) ;    }    vnGraph[0][1] = 10 ;    vnGraph[0][3] = 30 ;    vnGraph[0][4] = 100 ;    vnGraph[1][2] = 50 ;    vnGraph[2][4] = 10 ;    vnGraph[3][2] = 20 ;    vnGraph[3][4] = 60 ;
    BBShortestDijkstra bbs (vnGraph) ;    bbs.doDijkatra () ;}

 

 

贪心算法三个核心问题

 

第一个问题：为什么不直接求全局最优解?

 

1.原问题复杂度过高；

2.求全局最优解的数学模型难以建立；

3.求全局最优解的计算量过大；

4.没有太大必要一定要求出全局最优解，“比较优”就可以。

 

第二个问题：如何把原问题分解成子问题？

 

1、按串行任务分

时间串行的任务，按子任务来分解，即每一步都是在前一步的基础上再选择当前的最优解。

 

2、按规模递减分

规模较大的复杂问题，可以借助递归思想（见第2课），分解成一个规模小一点点的问题，循环解决，当最后一步的求解完成后就得到了所谓的“全局最优解”。

 

3、按并行任务分

这种问题的任务不分先后，可能是并行的，可以分别求解后，再按一定的规则（比如某种配比公式）将其组合后得到最终解。

 

第三个问题：如何知道贪心算法结果逼近了全局最优值？

 

这个问题是不能量化判断的，正是因为全局最优值不能够知道，所以才求的局部最优值。追求过程需要考虑以下几个问题:

1.成本

耗费多少资源，花掉多少编程时间。

 

2.速度

计算量是否过大，计算速度能否满足要求。

 

3.价值

得到了最优解与次优解是否真的有那么大的差别，还是说差别可以忽略。

 

 

审核编辑 ：李倩