

排序算法merge-sort的基础知识
描述
数据科学家每天都在处理算法。然而,数据科学学科作为一个整体已经发展成为一个不涉及复杂算法实现的角色。尽管如此,从业者仍然可以从对算法的理解和掌握中获益。
本文介绍、解释、评估和实现了排序算法merge-sort 。本文的目的是为您提供有关合并排序算法的可靠背景信息,该算法是更复杂算法的基础知识。
尽管合并排序不被认为是复杂的,但是理解该算法将有助于您认识到选择最有效的算法来执行与数据相关的任务时需要考虑的因素。创建于 1945 年的 约翰·冯·诺依曼 使用分治方法开发了合并排序算法。
分而治之
要理解合并排序算法,您必须熟悉分治范式,以及递归的编程概念。计算机科学领域中的递归是指定义用于解决问题的方法在其实现体中调用自身。
换句话说,函数会反复调用自身。
图 1 。递归的视觉图解——作者的图像 .
分治算法(合并排序是一种)在其方法中使用递归来解决特定问题。分治算法将复杂问题分解为更小的子部分,其中定义的解决方案递归地应用于每个子部分。然后分别求解每个子部分,并重新组合解决方案以解决原始问题。
分而治之的算法设计方法结合了三个主要元素:
将较大的问题分解为较小的子问题。(分开)
递归使用函数来解决每个较小的子问题。(征服)
最终的解决方案是对较大问题的较小子问题的解决方案的组合。(合并)
其他算法使用分治范式,如快速排序、二进制搜索和 Strassen 算法。
合并排序
在按升序对列表中的元素进行排序的上下文中, merge-sort 方法将列表分成两半,然后迭代新的两半,不断地将它们进一步分成更小的部分。
随后,对较小的一半进行比较,并将结果组合在一起,形成最终的排序列表。
步骤和实施
合并排序算法的实现分为三步。分而治之,然后结合。
分而治之方法的分而治之部分是第一步。这个初始步骤将整个列表分成两个较小的部分。然后,列表被进一步分解,直到它们不能再被分割,在每个减半的列表中只留下一个元素项。
合并排序的第二阶段中的递归循环与按特定顺序排序的列表元素有关。在这种情况下,初始数组按升序排序。
在下图中,您可以看到合并排序算法中涉及的分割、比较和组合步骤。
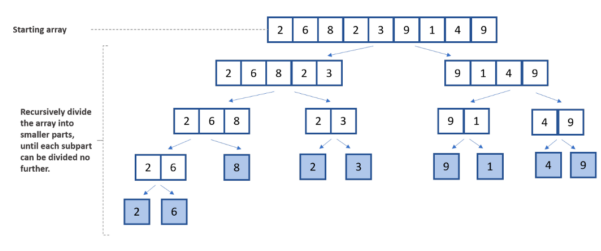
图 2 。按作者划分合并排序算法图像的组件插图。
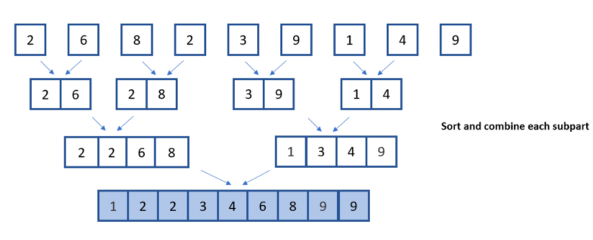
图 3 。征服和结合的组成部分形象的作者。
要自己实现这一点:
创建一个名为 merge _ sort 的函数,该函数接受整数列表作为参数。以下所有说明均在此功能范围内。
首先把清单分成两半。记录列表的初始长度。
检查记录的长度是否等于 1 。如果条件的计算结果为 true ,则返回列表,因为这意味着列表中只有一个元素。因此,不需要划分清单。
获取元素数大于 1 的列表的中点。使用 Python 语言时,//执行除法,不带余数。它将除法结果四舍五入到最接近的整数。这也被称为楼层划分。
使用中点作为参考点,将列表拆分为两半。这是分而治之算法范例的分而治之的一面。
Recursion is leveraged at this step to facilitate the division of lists into halved components. The variables ‘left_half’ and ‘right_half’ are assigned to the invocation of the ‘ merge_sort’ function, accepting the two halves of the initial list as parameters.
“ merge_sort ”函数返回对一个函数的调用,该函数将两个列表合并,以返回一个组合的排序列表。
- 序列表。
def merge_sort(list: [int]): list_length = len(list) if list_length == 1: return list mid_point = list_length // 2 left_half = merge_sort(list[:mid_point]) right_half = merge_sort(list[mid_point:]) return merge(left_half, right_half)
- 创建一个 ‘merge’ 函数,该函数接受两个整数列表作为其参数。此函数包含分治算法范例的征服和合并方面。以下所有步骤均在此函数体中执行。
- 为保存已排序整数的变量“ output ”分配一个空列表。
- 指针 ‘i’ 和 ‘j’ 分别用于为左列表和右列表编制索引。
- 在 while 循环中,对左列表和右列表的元素进行比较。每次比较后,输出列表将填充在两个比较的元素中。追加元素列表的指针递增。
- 要添加到排序列表的其余元素是从当前指针值到相应列表末尾的元素。
def merge(left, right): output = [] i = j = 0 while (i < len(left) and j < len(right)): if left[i] < right[j]: output.append(left[i]) i +=1 else: output.append(right[j]) j +=1 output.extend(left[i:]) output.extend(right[j:]) return output unsorted_list = [2, 4, 1, 5, 7, 2, 6, 1, 1, 6, 4, 10, 33, 5, 7, 23]
sorted_list = merge_sort(unsorted_list)
print(unsorted_list)
print(sorted_list)
性能和复杂性
大 O 表示法是一种标准,用于定义和组织算法在空间需求和执行时间方面的性能。
合并排序算法在最佳、最差和平均情况下的时间复杂度相同。对于大小为 n 的列表,合并排序算法要完成的预期步骤数、最小步骤数和最大步骤数都是相同的。
正如本文前面提到的,合并排序算法分为三个步骤:划分、征服和合并。“分割”步骤涉及到列表中点的计算,无论列表大小如何,它都只需要一个操作步骤。因此,该操作的符号表示为 O(1) 。
“征服”步骤包括划分和递归求解子数组—— logn 表示这一点。“合并”步骤包括将结果合并到最终列表中;此操作执行时间取决于列表大小,并表示为 O(n) 。
平均、最佳和最差时间复杂度的合并排序表示法是 log n * n * O ( 1 ) 。在大 O 表示法中,低阶项和常数可以忽略不计,这意味着合并排序算法的最终表示法是 O ( n 日志 n ) 。有关合并排序算法的详细分析,请参阅 article 。
评价
合并排序在对大型列表进行排序时表现良好,但在较小列表上使用时,其操作时间比其他排序解决方案慢。合并排序的另一个缺点是,即使初始列表已经排序,它也会执行操作步骤。在链表排序的用例中,合并排序是最快的排序算法之一。合并排序可用于外部存储系统(如硬盘)中的文件排序。
关键外卖
本文描述了合并排序技术,将其分解为组成操作和逐步过程。
合并排序算法是常用的,与其他排序算法相比,该算法背后的直觉和实现相当简单。本文包括 Python 中合并排序算法的实现步骤。
您还应该知道,在不同情况下,合并排序方法的执行时间的时间复杂度在最佳、最差和平均情况下保持不变。建议在以下情况下使用合并排序算法:
处理较大的数据集时,请使用合并排序算法。与其他排序算法相比,合并排序在小数组上的性能较差。
链表中的元素引用了列表中的下一个元素。这意味着在合并排序算法操作中,指针是可修改的,使得元素的比较和插入具有恒定的时间和空间复杂性。
确定数组是未排序的。即使在排序的数组上, Merge-sort 也会执行其操作,这是对计算资源的浪费。
当考虑到数据的稳定性时,使用合并排序。稳定排序涉及保持数组中相同值的顺序。与未排序的数据输入相比,稳定排序中整个数组中相同值的顺序在排序后的输出中保持在相同的位置。
关于作者
Richmond Alake 是一名机器学习和计算机视觉工程师,他与多家初创公司和公司合作,整合深度学习模型,以解决商业应用中的计算机视觉任务。
审核编辑:郭婷
- 相关推荐
- 热点推荐
- NVIDIA
-
Linux的sort命令介绍2024-04-08 505
-
VHDL中的排序算法怎么实现?2019-03-29 2641
-
C语言中的排序算法了解2018-11-12 3100
-
Linux系统中sort排序命令的使用教程2019-04-02 687
-
C++基础语法十大排序算法后五个分享2021-10-08 1649
-
嵌入式开发者都该了解的10大算法2022-06-16 1264
-
关于JAVA的相关基础知识2022-09-23 483
-
利用强化学习来探索更优排序算法的AI系统2023-06-19 1364
-
使用C++ sort函数对vector进行自定义排序2023-07-22 2656
-
list.sort()排序比stream().sorted()排序性能更好吗?2023-08-09 1501
-
排序算法有哪些2023-10-11 1338
-
sort函数python用法2023-11-21 2859
-
十大排序算法总结2023-12-20 2067
-
C语言实现经典排序算法概览2024-02-25 961
-
详解Linux sort命令之掌握排序技巧与实用案例2025-01-09 1645
全部0条评论

快来发表一下你的评论吧 !

