梯度下降和反向传播算法助于ANN从数据集中学习

人工神经网络 （ ANN ）是 人工智能（ AI ） 技术的基本构件。人工神经网络是 machine-learning 模型的基础；它们模拟的学习过程与人脑相同。简言之，人工神经网络赋予机器完成特定任务的类似于人的性能（以及更高性能）的能力。本文旨在为数据科学家提供基本的高级知识，以了解在训练 ANN 时调用的函数和方法所涉及的低级操作。

作为数据科学家，我们的目标是通过暴露数据中的模式来解决业务问题。通常，这是通过使用机器学习算法来识别模式和以模型表示的预测来完成的。为特定用例选择正确的模型，并适当地调整参数，需要彻底了解问题和底层算法。对问题域和算法的理解是需要考虑的，以确保我们正确使用模型，并正确解释结果。

本文介绍并解释了梯度下降和反向传播算法。这些算法有助于 ANN 从数据集中学习，特别是在涉及数据点和神经网络预测的操作导致网络参数值发生修改的情况下。

建立直觉

在我们进入这篇文章的技术细节之前，让我们先看看人类是如何学习的。

人类大脑的学习过程是复杂的，研究几乎没有触及人类学习的表面。然而，我们所知道的很少的东西对构建模型是有价值和有帮助的。与机器不同，人类不需要大量数据来理解如何解决问题或做出逻辑预测；相反，我们从经验和错误中学习。

人类通过突触可塑性的过程学习。突触可塑性是一个术语，用来描述获得新信息后新的神经连接是如何形成和加强的。就像我们在经历新事件时大脑中的连接得到加强和形成一样，我们通过计算神经网络预测的误差来训练人工神经网络，并根据这些误差加强或削弱神经元之间的内部连接。

梯度下降

梯度下降是一种标准的优化算法。它通常是第一个用于训练机器学习的优化算法。让我们剖析“梯度下降”这个术语，以便更好地理解它与机器学习算法的关系。

坡度是对直线或曲线的陡度进行量化的测量。从数学上讲，它详细说明了直线上升或下降的方向。下降是向下的动作。因此，梯度下降算法根据这些短语的两个简单定义量化向下运动。

为了训练机器学习算法，您需要努力识别网络中的权重和偏差，以帮助您解决所考虑的问题。例如，您可能有分类问题。查看图像时，需要确定图像是猫还是狗。为了建立模型，您需要使用正确标记的猫和狗图像数据样本来训练算法。

虽然上面描述的示例是分类，但问题可能是定位或检测。尽管如此， well 神经网络在问题上的表现被建模为一个函数，更具体地说，是一个成本函数；成本或有时被称为损失函数的东西衡量模型的错误程度。成本函数的偏导数影响最终模型的权重和选择的偏差。

梯度下降是一种算法，有助于搜索参数值，使代价函数最小化，以达到局部最小或最优精度。

神经网络中的代价函数、梯度下降和反向传播

神经网络令人印象深刻。同样令人印象深刻的是，计算程序能够区分图像和图像中的对象，而无需明确告知要检测的特征。

将神经网络视为接受输入（数据）以产生输出预测的函数是有帮助的。这个函数的变量是神经元的参数或权重。

因此，解决交给神经网络的任务的关键任务是以近似或最好地代表数据集的方式调整权重和偏差的值。

下图描绘了一个接收输入（ X ）的简单神经网络1十、2十、3十、N） ，这些输入被转发到包含权重（ W ）的层内的神经元1W2W3WN） 。输入和权重经过乘法运算，结果通过加法器（）相加，激活函数调节层的最终输出。

 

 

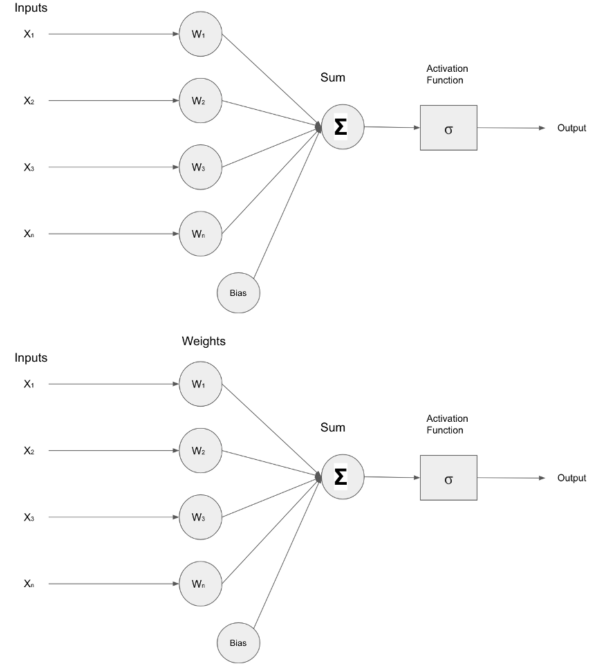
图 1 ：作者创建的浅层神经网络的图像。

为了评估神经网络的性能，需要一种机制来量化神经网络预测和实际数据样本值之间的差异或差距，从而计算出影响神经网络内权重和偏差修改的因素。

cost function 简化了神经网络预测值和数据样本实际值之间的误差差距。

 

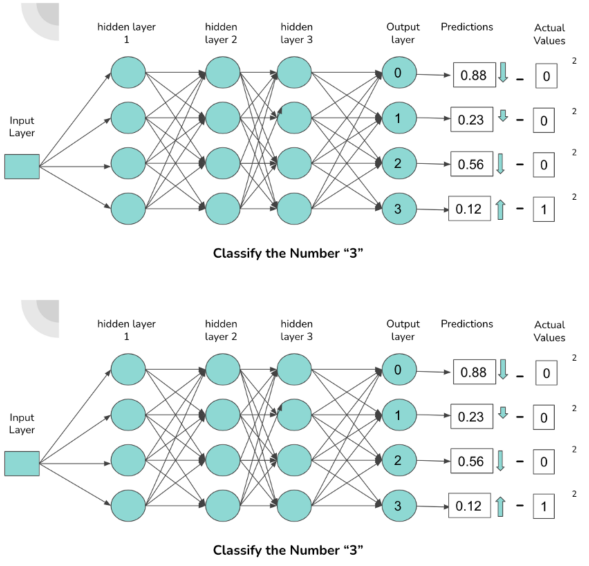
图 2 ：描述的神经网络内部连接和预测。

上图展示了一个由密集连接的神经元组成的简单神经网络结构，它对包含数字 0-3 的图像进行分类。输出层中的每个神经元对应一个数字。与神经元连接的激活程度越高，神经元输出的概率就越高。概率对应于通过网络前馈的数字与激活的神经元相关联的可能性。

当一个“ 3 ”通过网络前馈时，我们期望负责分类“ 3 ”的连接（由图中的箭头表示）具有更高的激活度，这导致与数字“ 3 ”相关的输出神经元的概率更高。

神经元的激活有几个因素，即偏差、权重和前一层的激活。为了使神经网络在特定数据集上获得最佳性能，必须对这些指定的组件进行迭代修改。

通过利用“均方误差”等成本函数，我们获得了与网络误差有关的信息，用于通过网络的权重和偏差向后传播更新。

为完整起见，以下是机器学习中使用的成本函数示例：

均方误差

范畴交叉熵

二元交叉熵

对数损失

我们已经介绍了如何通过测量网络预测的技术来提高神经网络的性能。本文的其余内容主要关注梯度下降、反向传播和成本函数之间的关系。

图 3 中的图像显示了绘制在 x 轴和 y 轴上的成本函数，该函数的参数空间中包含值。让我们来看看神经网络是如何学习的，它将代价函数可视化为一个不均匀的曲面，绘制在一个图上，在可能的权重/参数值的参数空间内。

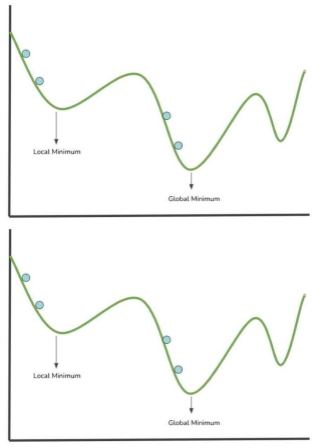
图 3 ：可视化的梯度下降。

上图中的蓝色点表示搜索局部最小值的步骤（将参数值计算到成本函数中）。建模成本函数的最低点对应于导致成本函数最低值的权重值的位置。代价函数越小，神经网络的性能越好。因此，可以根据收集的信息修改网络的权重。

梯度下降法是一种算法，用于引导在每一步中选择的成对值朝着最小值移动。

局部最小值：成本函数指定范围或扇区内的最小参数值。

全局最小值：这是整个成本函数域内的最小参数值。

梯度下降算法通过计算可微函数的梯度并沿梯度的相反方向移动，指导搜索以局部/全局最小值最小化函数的值。

反向传播是一种机制，通过这种机制，可以反复调整影响神经元输出的组件（偏差、权重、激活），以降低成本函数。在神经网络的结构中，神经元的输入，包括与前一层神经元的所有先前连接，决定了它的输出。

反向传播涉及的关键数学过程是导数的计算。反向传播操作计算成本函数相对于权重、偏差和前一层激活的偏导数，以确定哪些值会影响成本函数的梯度。

通过计算梯度使代价函数最小化，得到局部极小值。在每个迭代或训练步骤中，网络中的权重通过计算的梯度以及 learning rate 进行更新，该梯度控制对权重值的修改因子。在神经网络的训练阶段，每个步骤都要重复这个过程。理想情况下，目标是在每一步之后更接近局部最小值。

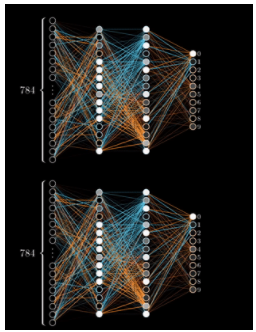
图 4 ：错误的反向传播（反向传播）。

“反向传播”这个名字来源于进程的字面意思，即“错误的反向传播”。梯度的偏导数量化了误差。通过在网络中向后传播误差，最后一层（距离输出层最近的层）梯度的偏导数用于计算第二层到最后一层的梯度。

误差在各层中传播，并利用当前层中前一层的梯度偏导数，直到到达网络中的第一层（距离输入层最近的层）。

总结

这只是梯度下降主题的入门。有一个数学和微积分的世界与梯度下降相关。

TensorFlow 、 SciKit-Learn 、 PyTorch 等软件包通常会抽象出实现训练和优化算法的复杂性。然而，这并不能免除数据科学家和 ML 从业者理解这些智能“黑匣子”背后发生的事情的要求。

关于作者

Richmond Alake 是一名机器学习和计算机视觉工程师，他与多家初创公司和公司合作，整合深度学习模型，以解决商业应用中的计算机视觉任务。

审核编辑：郭婷