如何对一维数组做maxpooling

　　大家好，我是梁唐。

　　最近在剑指offer里看到一道算法题很有意思，分享给大家。

　　题面很简单，只有一句话，叫做对一维数组做maxpooling。

　　可能很多同学不知道pooling是什么意思，pooling是深度学习中的一个术语，翻译过来叫做池化。池化的目的是压缩张量的规模，张量可以理解成是矩阵。

　　池化的时候会将一个小窗口在矩阵上移动，每次会对小窗口内的元素进行计算，得到一个值。不同的池化方法体现在这里的计算的方式不同，比如常见的maxpooling，指的是每次从窗口中找出最大值的操作，再比如常见的sumpooling，则是进行求和计算。

　　我们可以看下下图，就是一个典型的maxpooling的操作。

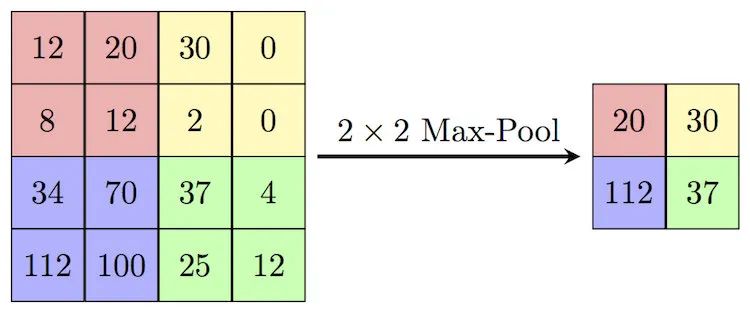
　　池化的时候，窗口的大小是2x2，移动的步长是2，每次都取出这2x2个数中的最大值，因此叫做最大值池化，英文就是maxpooling。

　　很明显经过池化之后，矩阵的大小大大压缩了，如果使用2x2的规模进行池化，得到的结果是原本的1/4。一般在卷积神经网络当中，由于原始的输入规模比较大(图片或者是视频)，所以会反复进行池化，将原始的张量反复压缩，提取出最核心的特征点。

　　那如果是一维的池化怎么操作呢，其实是一样的，只不过窗口也换成了一维的而已。

　　比如说我们有这样一个数组：[12, 20, 30, 0]，窗口大小是2，步长是1，那么池化得到的结果是[20, 30, 30]。

　　介绍完了pooling的概念之后，我们再回到题目本身：给定一个长度为n的数组，再给定一个整数k，要求以k为窗口长度步长为1进行maxplooing之后的结果。

　　由于步长为1，所以我们一共要求n-k+1个最大整数，每次求最大整数如果采用遍历的话，需要遍历k个元素。那么整体就是，极端情况下，比如k=n/2时，问题的复杂度为。

　　这个只是暴力求解的方法，显然在面试的时候这样的答案是无法让面试官满意的，我们必须要想出更快的方法来。

　　我们简单分析一下问题会发现，如果我们把窗口滑动看成是一次求解区间最大值的操作，那么这样的操作数是固定的，也就是n-k+1，这个数字是固定的，是我们无法改变的。所以如果想要优化复杂度的话，只能从另外一个维度，也就是每次求解时的计算复杂度入手。

　　在暴力的方法下，我们每次遍历k个元素，找到最大值。稍微分析一下就会发现，这里面有大量的重复。因为窗口的步长为1，假设某一次窗口内的元素是，移动之后的元素就是，当中有k-1个元素是重复的。

　　不难看出，对于每个元素来说，它最多会在k个窗口当中出现。对于每一个窗口我们都遍历了一次，其实是没有必要的，这当中存在大量的冗余。所以我们要做的就是想办法优化它，尽量让每个元素只会遍历一次，或者是遍历常数次。

　　你看，虽然我们现在还是没有想出解法，但是我们通过分析问题，已经找到了方向，正在一步步逼近答案。

　　顺着这个思路我们可以想到，我们可以维护上一个区间的最大值，我们假设这个最大值是m，然后和当前区间新加入的元素进行对比，大的那个就是当前区间的答案。

　　思路上看起来貌似可以，但细节上有一些问题。首先，上一个区间的最大值是可能会过期的。比如上一个区间刚好第一个元素最大，而当前区间第一个元素是，并不在当前区间里，所以是不能作为答案的。

　　我们是可以很容易判断上一个区间的最大值有没有过期的，但问题在于如果这个答案过期了，我们就抓瞎了，不知道哪个值是答案了。

　　那要怎么解决呢?

　　其实也很简单，我们维护一个最大值会存在过期的问题，那干脆我们维护多个最大值嘛，我们维护多个答案，即使刚好因为区间移动有一个最大值过期了，还有第二个能够顶上，这样不就OK了吗?

　　的确，这样就搞定了，整个思路基本上就贯穿了。剩下的问题就是多个最大值如何维护的问题了，由于要维护多个值，我们自然需要一个数据结构来存储，只用几个变量是不行的了。

　　对于这个数据来说，我们读到了新的数据时要很方便插入，对于之前过期的答案我们也要很方便移除，同时还要保证运行效率。在这几个要求的结合之下，只剩下双端队列这一个选项了。

　　能想到双端队列，基本上这题就做出一大半了。

　　剩下的问题就是怎么使用它，由于我们的目的是找到最大值，并且是尽量快地找到合适的最大值，比较容易想到我们可以将双端队列设计成有序的。我们每次从最大值开始判断，如果它还在窗口内，就是答案，如果已经超出了，就将它抛弃判断第二大，循环往复直到找到答案。

　　最后还剩下两个小问题，第一个小问题是我们怎么判断最大值是否过期?

　　很简单，我们在存储的时候可以不用存元素的值，而存元素的下标。通过下标就可以很轻易判断它是否在窗口内，如果不在，那么自然说明已经过期了。

　　第二个问题是，每次移动窗口之后读入新的值如何更新?这也很简单，我们可以从末尾开始替换掉双端队列中比它小的元素。这样既更新了队列，又保证了队列的有序性。

　　闲言少叙，我们直接来看代码：

void get_max_pooling(int n, int k, vector<int> &nums, vector<int>& ans) {
    deque<int> dque;
    // 读入前k个元素
    for (int i = 0; i < k-1; i++) {
        int u = nums[i];
        // 从队列右侧插入，替换掉比它小的元素，保证有序性
        while (!dque.empty() && u > nums[dque.back()]) {
            dque.pop_back();
        }
        // 插入元素的下标而非具体的值
        dque.push_back(i);
    }
    for (int i = k-1; i < n; i++) {
        int u = nums[i];
        // 更新队列，操作同上
        while (!dque.empty() && i - dque.front() >= k) {
            dque.pop_front();
        }
        // 从队首拿到第一个在窗口内的元素
        while (!dque.empty() && (u > nums[dque.back()] || i - dque.back() >= k)) {
            dque.pop_back();
        }
        dque.push_back(i);
        ans.push_back(nums[dque.front()]);
    }
}

　　从代码来看，这题的代码量并不大，实现起来也并不复杂，但胜在思路巧妙。也算是剑指offer当中一道非常经典出镜率很高的题。

　　如果大家看不明白，可以结合一下代码再回过头去看下算法推导的过程。算法胜在思路而非答案。

　　好了，关于这道题就先聊到这里，祝大家日拱一卒。

　　原文标题：剑指算法题，一维数组求maxpooling

　　文章出处：【微信公众号：算法与数据结构】欢迎添加关注!文章转载请注明出处。

　　审核编辑：汤梓红