

一种比线段树还高效的区间算法
描述
01 故事起源
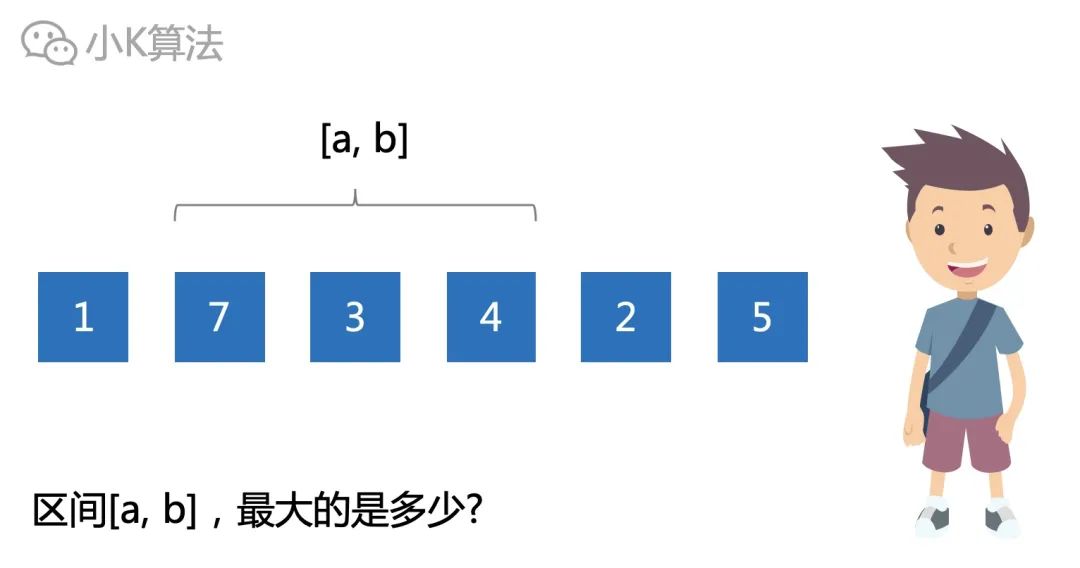
有N个数排列成一排,给定一个区间,如何快速找出区间内最大的数是多少呢?
02 分析
首先想到的自然是从区间头开始,依次遍历完区间内的元素,这样就可以找出结果了。但这个复杂度是O(n),肯定不是我们想要的。
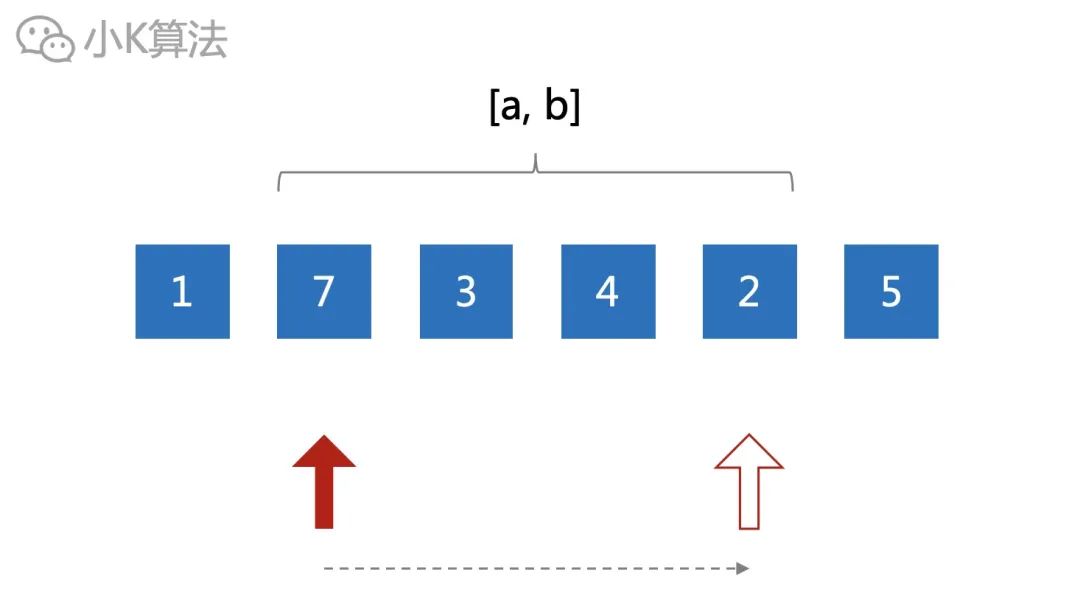
再来分析一下有什么特点呢?
这些数不会更改,所以每个区间的结果是不会变的,是否可以把所有的区间结果先计算出来?
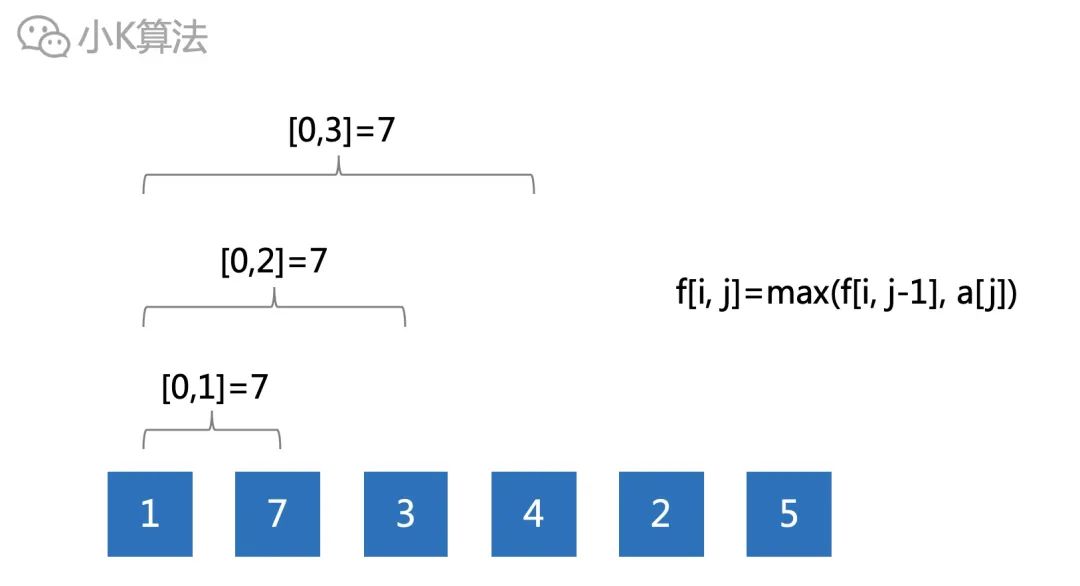
如果数据规模很小确实可以,一旦数据过大肯定就不行了,因为时间和空间都是O(n^2)。
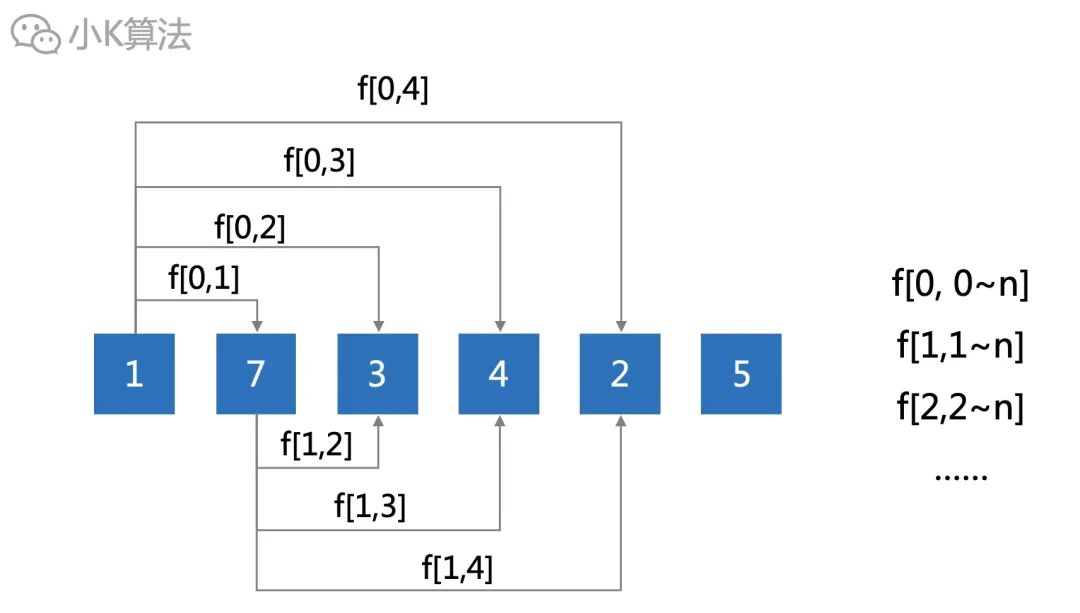
再考虑一下,区间的最值是有很强的传递关系,这就引导我们可以把大问题化为小问题。
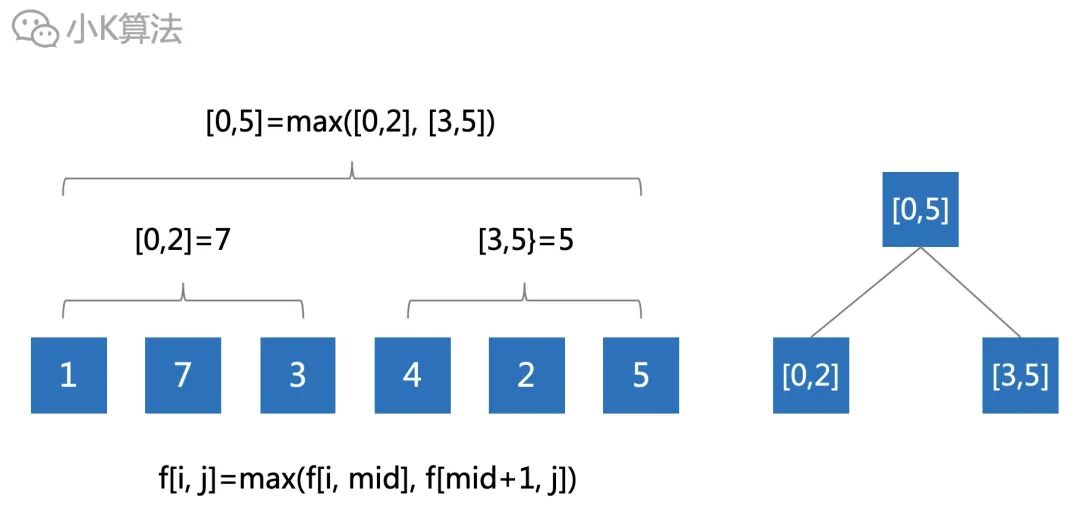
很显然,这就是一个标准的线段树模型,不过今天我们再换一个更加高效的算法,稀疏表。 03 稀疏表稀疏表的思想就是提前预处理数据,所以主要针对数据不变的情况,而线段树更加灵活,可以动态维护数据的变化。
首先还是将区间划分成很多的小区间。那如何划分更合理?
第2章节中,我们枚举了所有的区间情况,可以看出其实有很多重复的情况,比如下面[0,3]其实可以通过[0,1]和[2,3]组合出来。
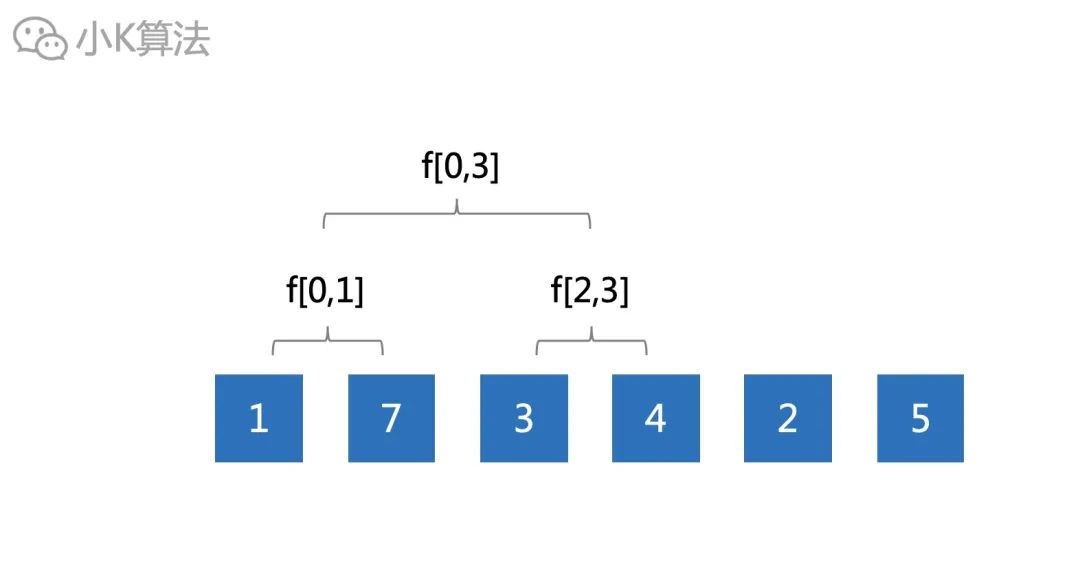
可以根据长度划分区间。
设数组为a[i],f[i][j]表示区间[i,j]的最大值。
则长度为1的区间总共有n个,f[i][i]=a[i]。
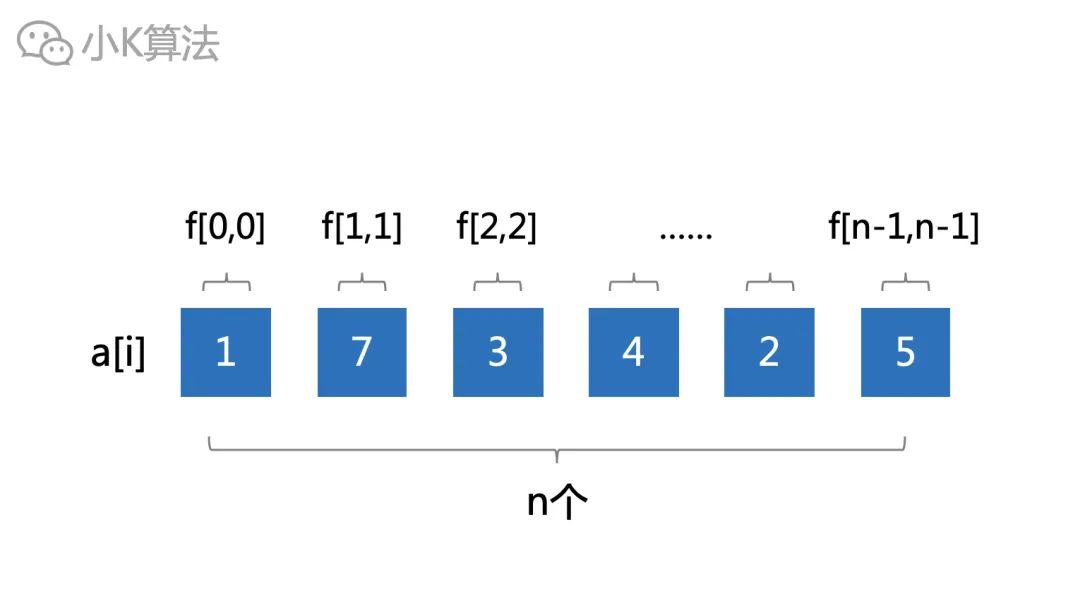
长度为2的区间总共有n-1个。
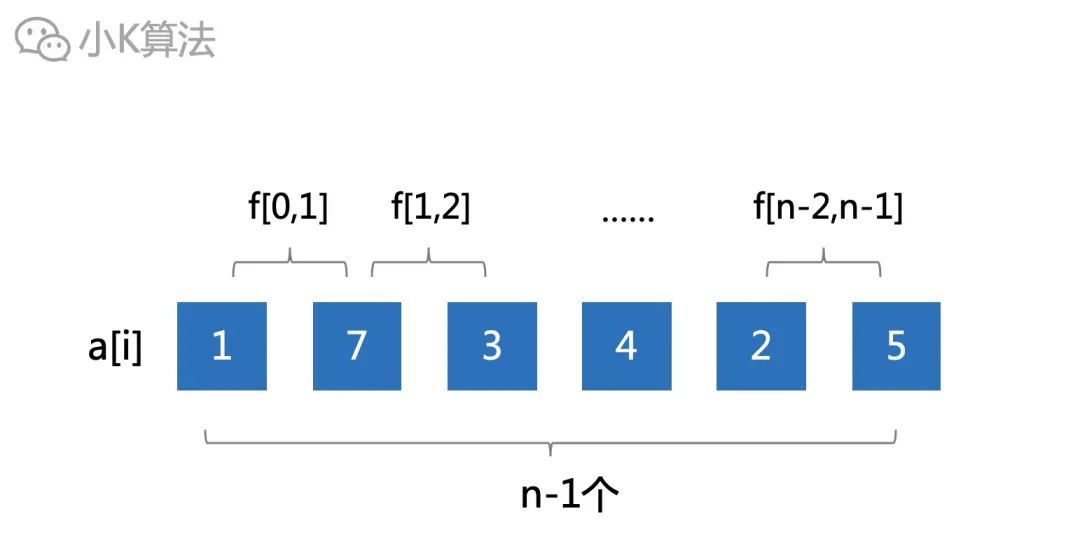
因为之前已经求出了长度为1的区间的最大值,所以区间长度为2的最大值可以通过区间长度为1的结果直接推出来。

接下来就考虑长度为3的区间了吗?
其实并不是,因为前面已经有了长度为1和2的,所以可以组合出长度为3和4的。
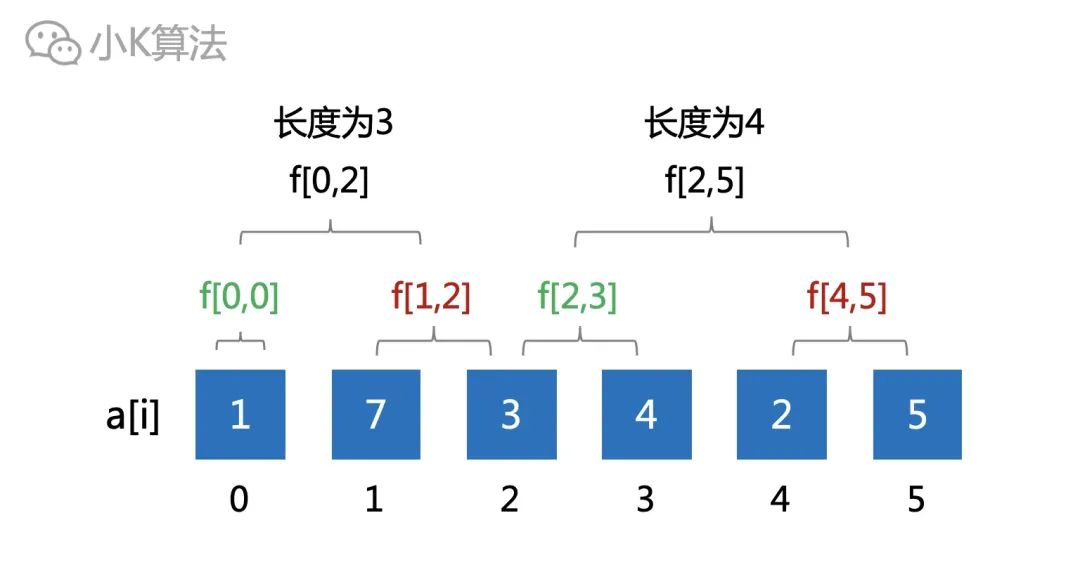
那就直接考虑长度为5的吗?
如果考虑为5的,那你怎么计算呢,前面的也推不出长度为5的结果啊,至少得有3个区间才能推出来
。
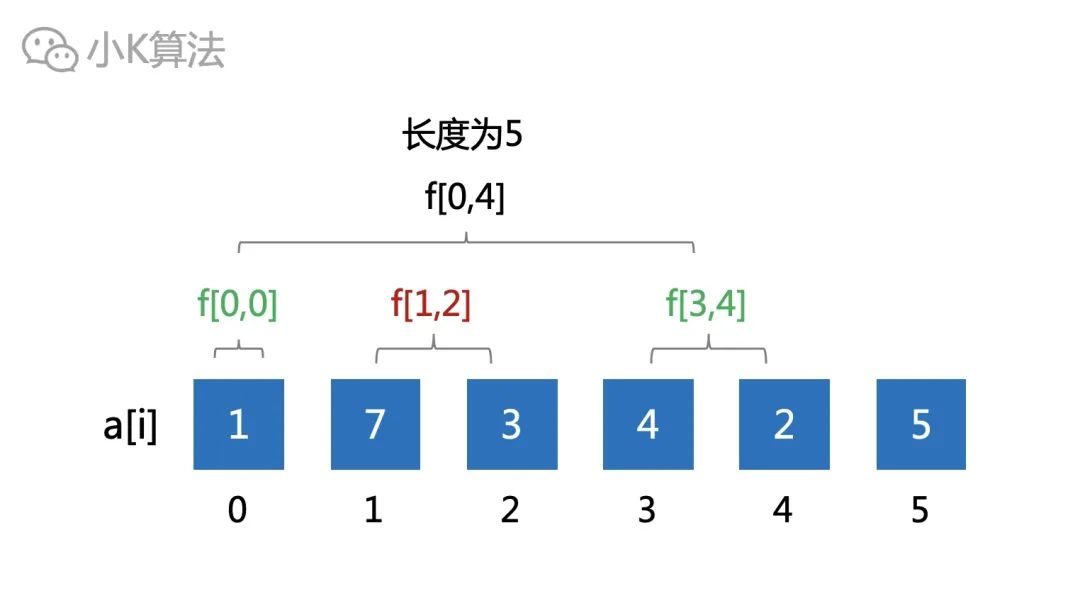
所以接下来考虑长度为4的区间才是正解,总共有n-3个。
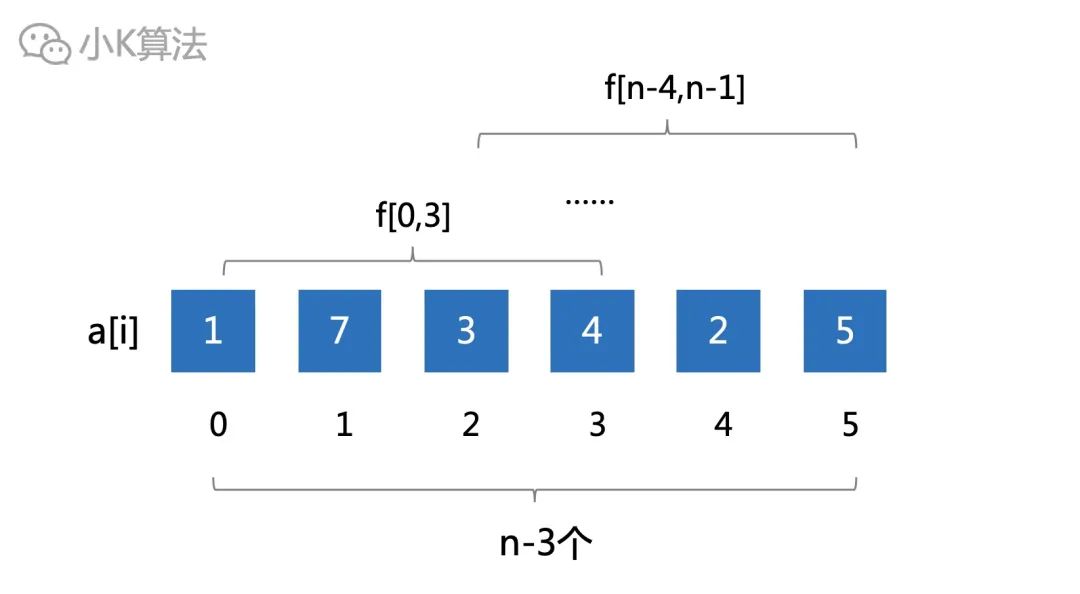
再接下来自然就是考虑长度为8的区间了,总共有n-7个。
但这里有个很明显的问题,就是我们的数组f[i,j]定义的不合理,因为里面很多的小区间没有用上,比如长度为3,5,6,7等,所以需要重新定义。 04 状态压缩可以将第二维用于表示区间长度,第一维表示区间起点,对第二维就可以进行状态压缩。
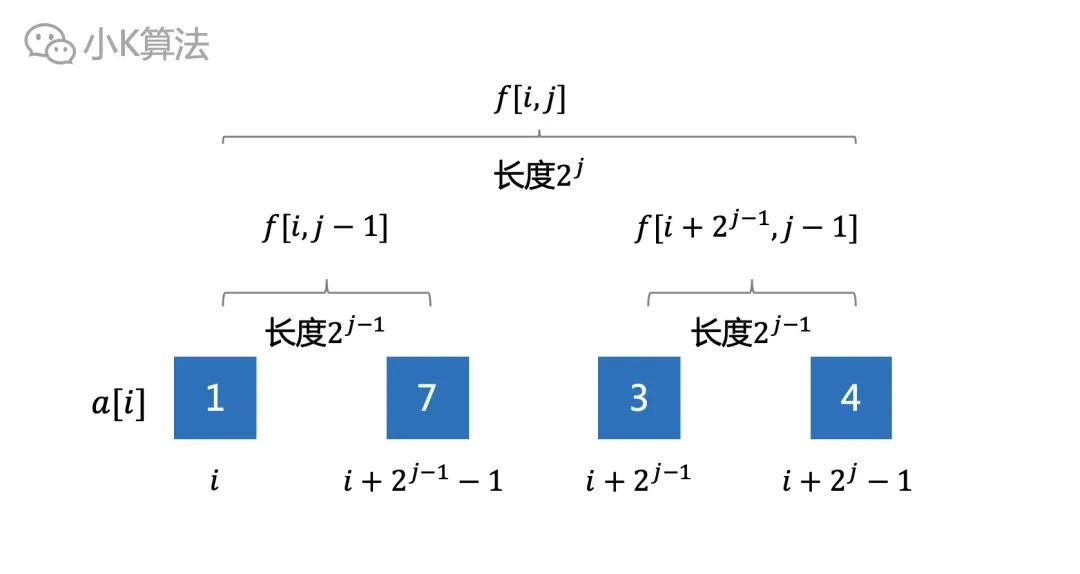
设f[i,j]表示从i开始,长度为2^j的区间的最大值,即区间[i,i+2^j-1]。
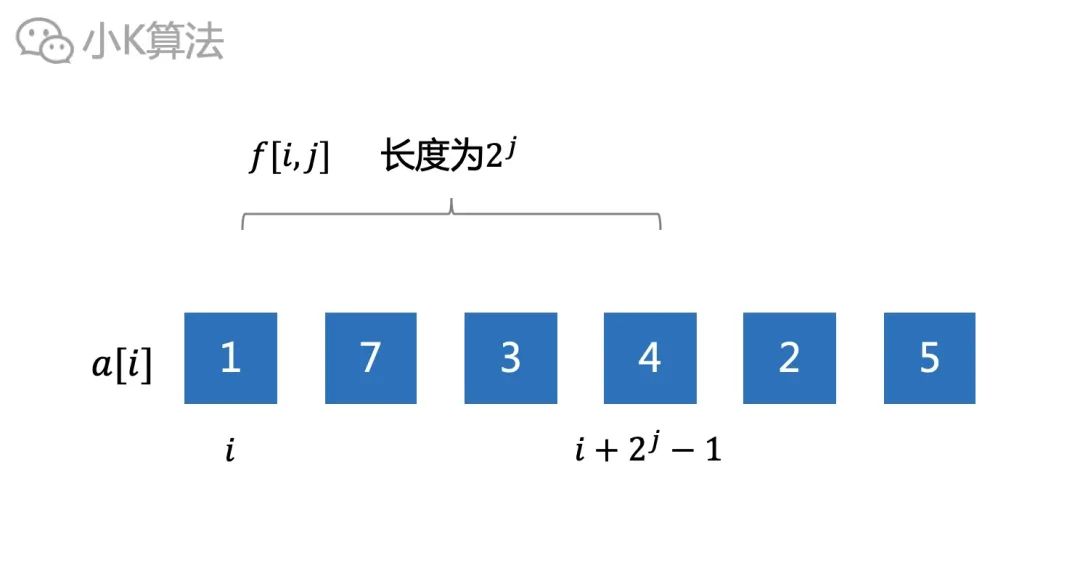
则长度为2^j的区间就可以通过左右2个长度为2^(j-1)的区间推出结果。时间和空间的复杂度都为O(nlogn)。
05 区间分解
那查询结果的时候要怎么处理呢,我们只计算了长度为2^j的区间,并没有计算长度为3、5、7等区间的结果。
所以这个处理和线段树的思想也类似,需要进行区间分解。不过线段树可能分解成很多个区间,而稀疏表只需要分解成2个区间就可以了。
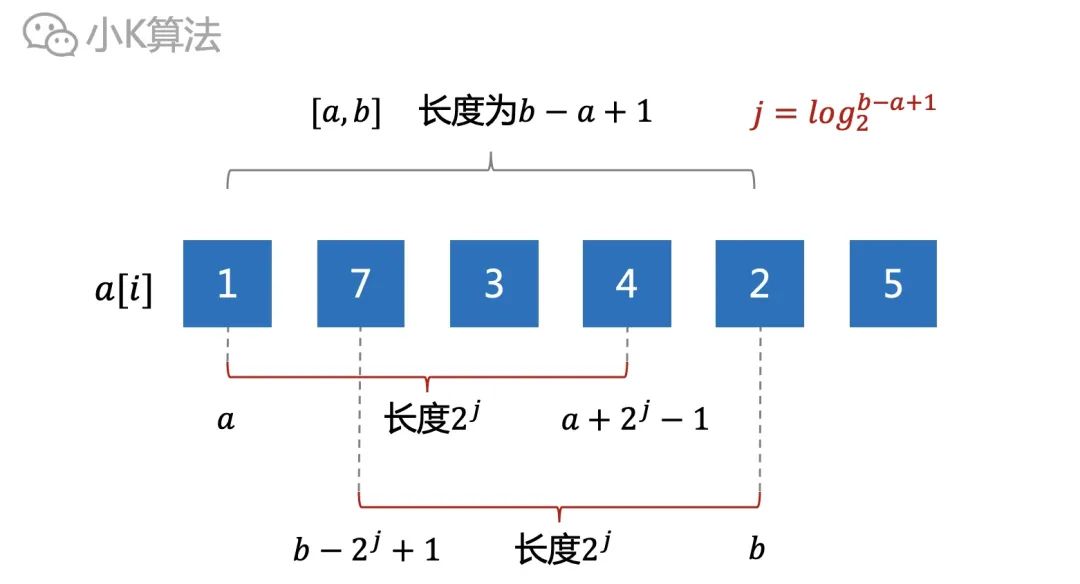
对于任意区间[a,b],长度为b-a+1,总可以找到2个长度为2^j的区间,这2个区间组合起来可以完全覆盖[a,b],其中j的值为log(b-a+1)。
左边的区间左端点从a开始,长度为2^j,即区间[a,a+2^j-1]。右边的区间右端点从b开始,长度为2^j,即区间[b-2^j+1,b]。
则区间[a,b]的最大值就是这两个区间中更大的那个,即max(f[a,j],f[b-2^j+1,j])。
06 代码实现
代码实现了最大值和最小值的获取。
6.1变量定义
int high[50000][17], low[50000][17], n, q;
6.1预处理
void solve() {
// 枚举区间长度,2^j《=n
for (int j = 1; (1 《《 j) 《= n; ++j) {
// 枚举左端点i,右端点i+2^j-1《=n-1
for (int i = 0; i + (1 《《 j) 《= n; ++i) {
high[i][j] = max(high[i][j - 1], high[i + (1 《《 (j - 1))][j - 1]);
low[i][j] = min(low[i][j - 1], low[i + (1 《《 (j - 1))][j - 1]);
}
} }
6.1main函数
int main() {
cin 》》 n 》》 q;
for (int i = 0; i 《 n; ++i) {
cin 》》 high[i][0];
low[i][0] = high[i][0];
}
solve();
for (int i = 0; i 《 q; ++i) {
int a, b;
cin 》》 a 》》 b;
a--;
b--;
int j = (int) (log(b - a + 1.0) / log(2.0));
int minHeight = min(low[a][j], low[b - (1 《《 j) + 1][j]);
int maxHeight = max(high[a][j], high[b - (1 《《 j) + 1][j]);
cout 《《 maxHeight - minHeight 《《 endl;
}
return 0; }
07 总结
对于数据不变的情况,可以用稀疏表预处理,这种属于离线算法。如果要动态维护变化,动态查询,那就得用在线算法,比如线段树。但稀疏表的效率确实高,有状态压缩和动态规划的思想,值得深入研究学习。
--- EOF ---
审核编辑 :李倩
-
深入理解线段树:线段树的区间修改与懒惰标记2023-10-13 1413
-
一种基于高效采样算法的时序图神经网络系统介绍2022-09-28 2815
-
一种基于伪ID码的树型防碰撞算法2021-05-13 771
-
一种动态区间的加权模糊聚类算法2021-04-13 1531
-
一种改进的线段分割检测算法2018-01-25 924
-
一种区间格的纵向合并算法2017-12-29 463
-
基于线段树的内存管理方法2017-12-27 979
-
哈夫曼算法的理解及原理分析,算法实现,构造哈夫曼树的算法2017-12-11 35132
-
基于逻辑区间热度的垃圾回收算法2017-12-05 755
-
一种新型的决策树剪枝优化算法2017-11-30 964
-
基于几何约束的视频帧间线段特征匹配算法2017-11-29 1028
-
一种新的多级能量异构WSNs簇优化算法2017-01-07 686
-
一种基于区间划分的风机故障预警方法2017-01-02 625
-
一种新的物理网络拓扑发现算法2010-02-09 737
全部0条评论

快来发表一下你的评论吧 !

