通过仿真校准压电传感器的方法

对声波进行检测和解释可以揭示物体中隐藏的有价值的信息。通过一些设备我们能够看到波的行为，例如压电 （PZT） 传感器。这些设备必须经过精心设计和校准，这个过程有时被称为测定。一个来自瑞士的研究团队使用多物理场仿真来测定用于材料和产品声学无损检测（NDT）的压电传感器。他们的项目向我们目展示了仿真如何帮助提高测定过程的效率，通过优化几何的网格划分，将模型的内存需求减少了一半，计算时间缩短了 5 倍！

声学无损检测：通过声音揭示隐藏的缺陷

无损检测描述了一种在不损坏物体的情况下揭示其重要属性的过程。这个过程是许多产品和系统的开发与质量控制的一个组成部分。无损检测方法通常通过施加能量脉冲来“检测”结构或材料。能量信号会因结构内部的裂缝或其他物理不规则性而改变，这些变化可以通过安装在结构上或附近的仪器来检测。例如，使用 主动热成像 对物体施加热量。内部不规则会导致热量分布发生意外变化，这些变化可以被测量并用于定位内部缺陷。

声发射 （AE） 分析是另一种重要的无损检测技术。当施加于固体物体时，超声波频率范围内的波会受到内部裂纹和其他不连续因素的影响。压电传感器可以检测到由此产生的声学信号变化，并产生电流作为机械压力的响应。怎样分析产生的信号并从中获取有用的信息是一项持续的挑战。

多物理场仿真是对声发射测试过程的自然补充。通过将实验数据纳入给定材料的模型，波传播模型以及压电传感器响应模型中，研究人员可以建立声学信号行为的模拟基线。基于断裂力学的材料缺陷模型，以及这些缺陷对模拟波行为的影响，可以帮助预测，在进一步测试中压电传感器如何响应这些实际存在的不连续性。随着最近科技的进步，这种模拟的计算需求已经大大减少。

压电传感器：记录球冲击试验的结果

无论是用于绘制地下断层线还是金属板内部的微观缺陷，声发射无损检测都需要对传感仪器进行精确测定。隶属于苏黎世联邦理工学院岩石物理与力学实验室的瑞士地震服务中心的研究人员在 COMSOL Multiphysics® 软件中构建了一个模型，测定用于板材球冲击测试的压电传感器，下图为在这些测试中使用的设备。

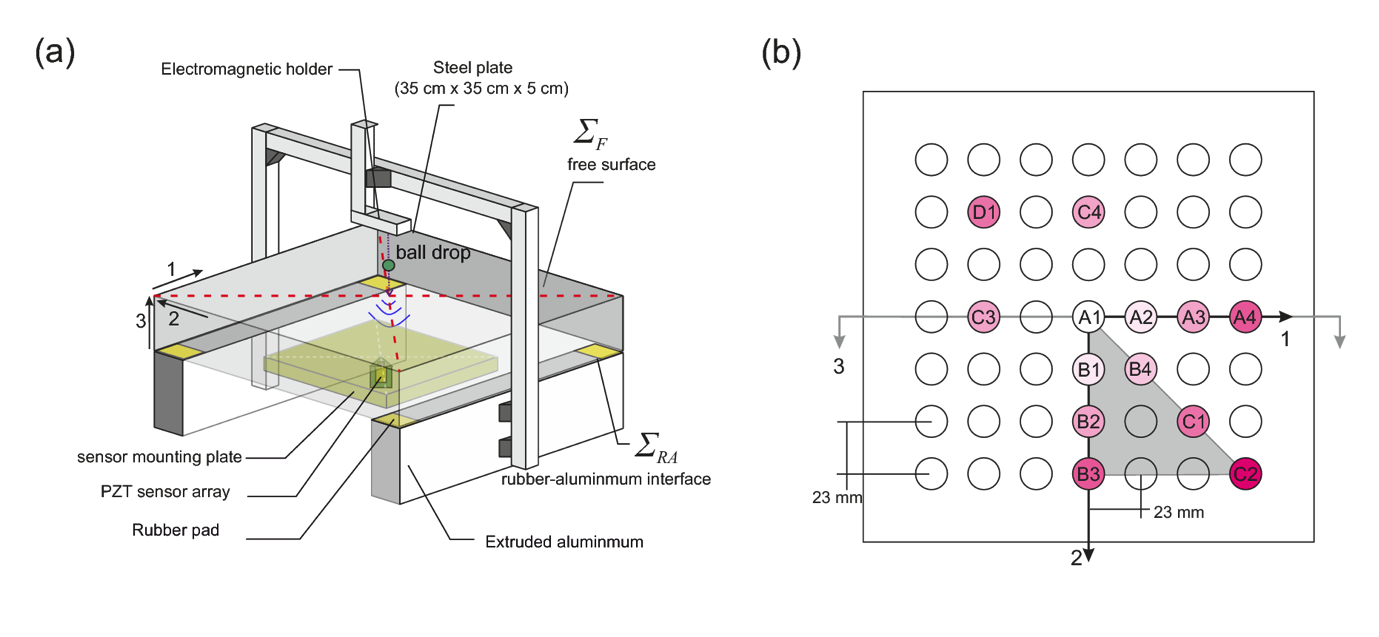
瑞士团队用于压电传感器实验测试的装置图（左）。传感器阵列相对于工件的布置（右）。图片由 R. Wu、PA Selvadurai、C. Chen 和 O. Moradian 提供。通过Springer 获得许可（CC BY 4.0）。

当用作测定过程的一部分时，不同大小的金属球将从测试仪器掉落到一个均匀的金属工件上。每个球的撞击都会产生超声频率范围内的声波。通过测量传感器在这些受控条件下的行为，研究人员可以获得用于数值测定过程的数据。

Wu 等人 （2021） 进行的落球测试示例。

间断伽辽金有限元建模：实现压电传感器的数值测定

为了从压电传感器跟踪的波行为中获得有用的信息，研究人员可以将测试结果与在半无限同质各向同性的弹性板内计算出的波传播进行比较。基于广义射线理论计算弹性应力波如何传播的过程被称为“兰姆问题”。对于给定材料的兰姆问题，其解称为“格林函数”，是由点力引起的应力波产生的弹性扰动值。

这些计算有助于建立测定压电传感器的基线，但这种方法的局限性很大。在发表于Journal of Nondestructive Evaluation 上的报告中，瑞士研究团队解释对此作了解释（参考文献 1）：

有两个主要问题限制了广义射线理论在计算格林函数方面的应用。首先，原位AE 事件振幅谱的角频率可能低至数百赫兹到数赫兹。［…］ 这需要大量的计算负荷才能获得大量可能的格林函数射线路径。其次，样品的有限性使得与兰姆问题相关的半无限条件对于实验室研究来说是不现实的。因此，来自有限弹性板的侧反射的射线路径不可忽略。

该团队通过 COMSOL Multiphysics 中的时域显式间断伽辽金有限元法 （dG-FEM） 建模解决了这些问题。基于仿真的方法，他们能够获得相当于一个有限的且真实世界里存在的测试案例中的有边界条件的格林函数的值。

优化网格：降低仿真的计算成本

压电测定模型是使用 COMSOL 软件中的 弹性波，时域显式 接口构建的，该接口可用于模拟弹性波在包含许多波长的大间隔传播。该模型在数值上计算了从 1kHz 到1MHz的真实格林函数，由 Heaviside 阶跃的力-时间函数激发。它使用相对精细的网格来寻找高频波的格林函数，并使用较粗的网格来寻找低频的格林函数。下面将进一步解释网格优化过程及其对计算效率的积极影响。

 

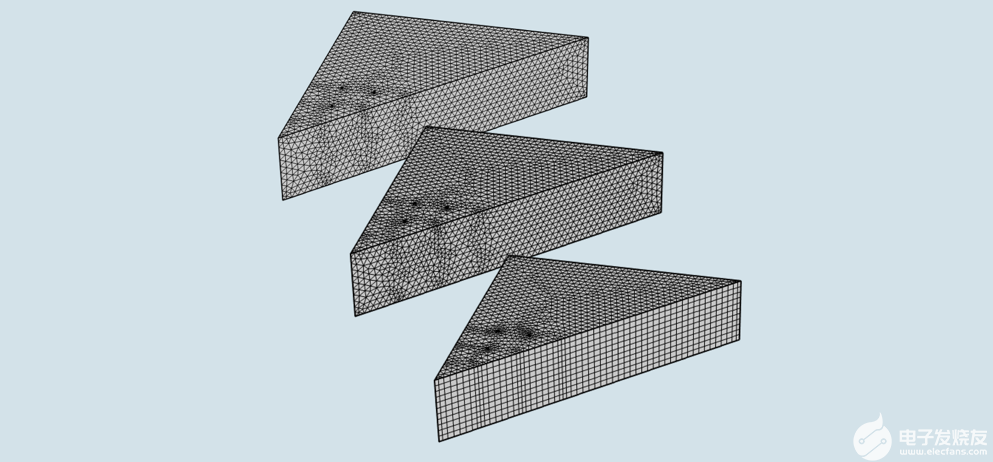
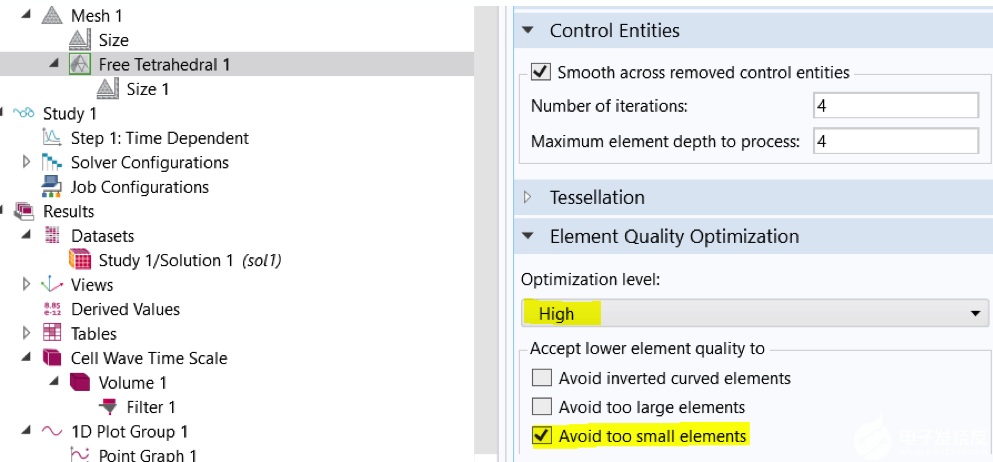
在模拟落球测试中，在一段工件上应用三个网格的图示。三个网格上较密的区域表示将安装 PZT 传感器的点。右图为”弹性波，时域显式”接口的截图，显示了避免过小单元的网格优化工具。

使用时域显式间断伽辽金有限元公式进行建模时，求解器采用的时间步长受相对于最大波速（通常是固体中的压力波速）的网格单元尺寸的最小值控制。这意味着，精细的网格划分对于获得最佳性能很重要。在左上图中，三个网格从上到下显示了优化过程中的渐进步骤。顶部的网格显示了对在实验室进行测试的压电传感器的一个自由四面体网格进行了细化。由于使用了避免过小的单元工具，中心网格显示出轻微的变化（计算时间减少了 2 倍）。在底部的网格中，我们看到了进一步的简化，因为三角形网格扫掠了 11 层水平面。结构化网格导致自由度降低，这有助于将模型的内存需求减少 2 倍，并将计算时间减少 5 倍。

当然，如果简化的网格会影响模型性能，那就没有用了。幸运的是，三个模型在两个测量点对模拟波的响应都显示出几乎相同的结果。通过使用较粗的网格来测量更长波长的模拟波，可以实现进一步的优化，如下图所示。

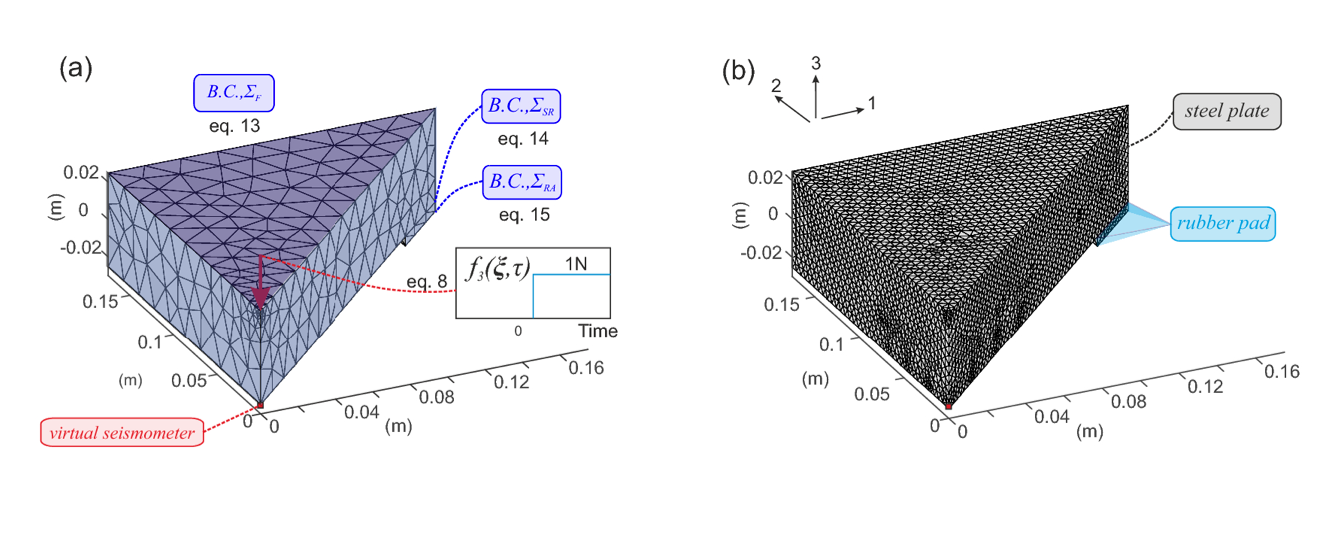
左侧是用于模拟低频波在模拟钢板上传播的粗网格。高频模拟波的行为是使用右侧显示的更精细的网格捕获的。图片由 R. Wu、PA Selvadurai、C. Chen 和 O. Moradian 提供。通过 Springer 获得许可（CC BY 4.0）。

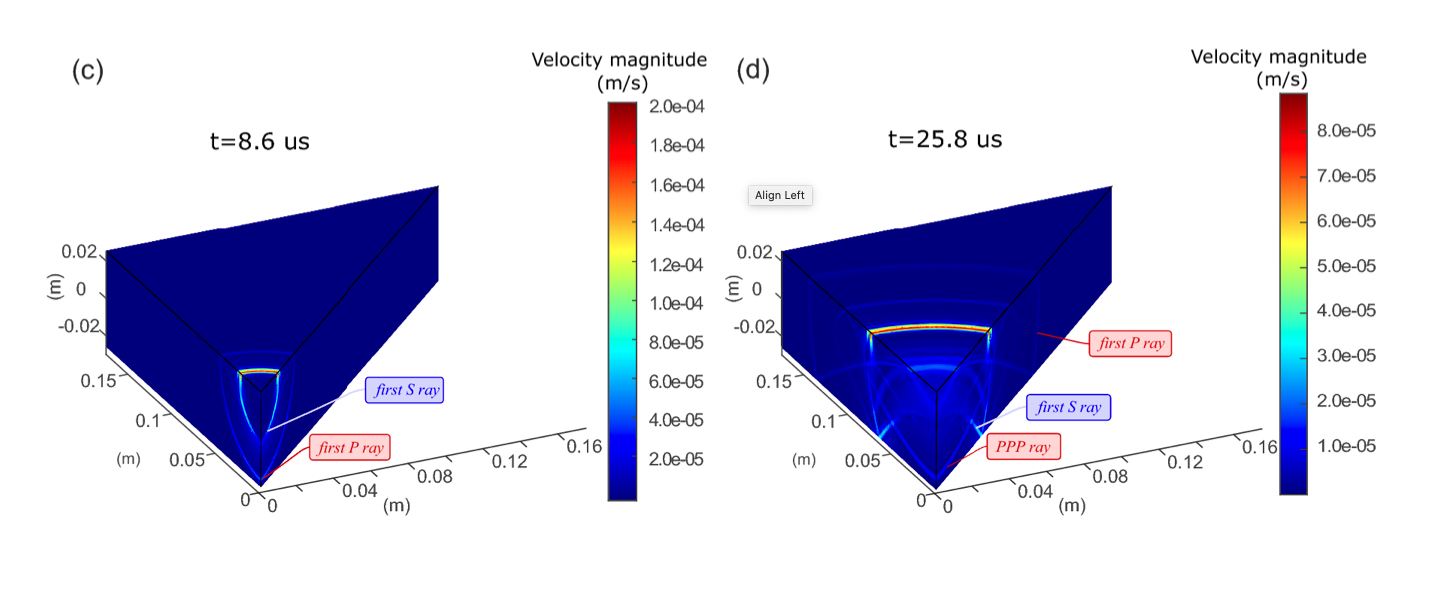
使用细网格模型模拟的粒子运动速度场的大小，分别为 8.6 纳秒（左）和 25.8 纳秒（右）。图片由 R. Wu、PA Selvadurai、C. Chen 和 O. Moradian 提供。通过 Springer 获得许可（CC BY 4.0）。