CCM和DEM中直流偏移的推导和描述

随着转换器设计对可靠性和尺寸考虑的日益重视，陶瓷电容器在 NB 应用中越来越受欢迎。因此，开发了高级恒定导通时间 （ACOT®） 控制拓扑，以在无需复杂外部补偿网络的情况下为陶瓷输出电容器提供稳定运行。一般来说，稳定性始终是设计师最关心的问题。在很多情况下，为了扩大反馈回路的噪声容限和瞬态速度，传统的分压器被前馈补偿器所取代。然而，由于输出的谷值控制，输出电压会产生额外的直流偏移，该偏移来自输出电压纹波和前馈补偿器。尤其，前馈补偿器的不同极点和零点位置会使反馈信号失真和相位移动。这可能会影响输出电压的调节精度和最大值。在本应用笔记中，将介绍和讨论有关直流偏移的详细分析和推导。

一、ACOT®控制与前馈补偿器简介

在开始计算直流偏移量之前，值得留出一些时间来介绍和了解 ACOT® 控制拓扑的机制。此外，前馈补偿器的特性和对反馈信号的影响将在后面讨论。

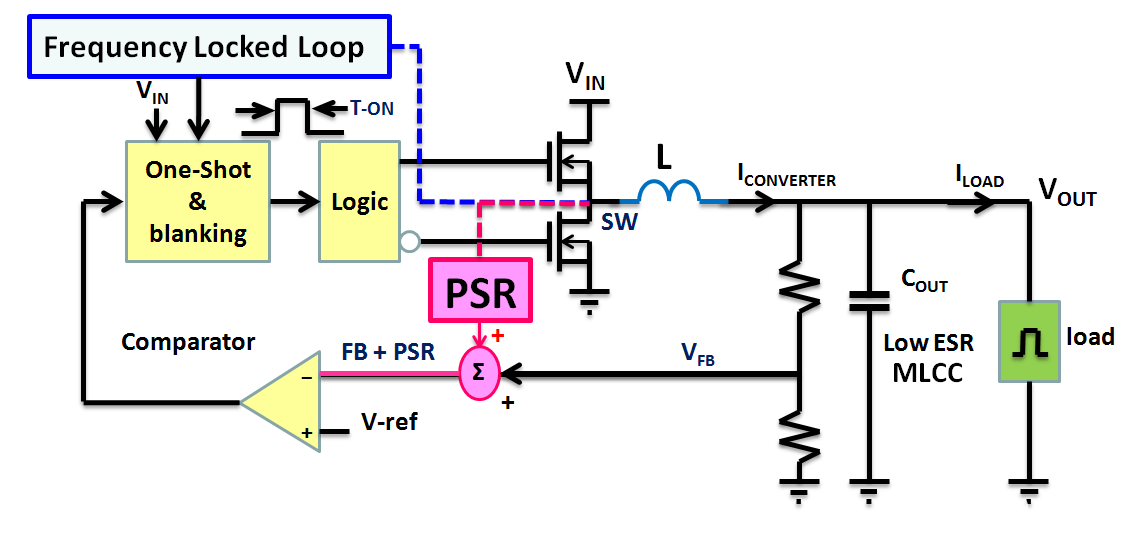
图1. 采用 ACOT® 控制方法的降压转换器

图 1 显示了标准 ACOT® 控制降压转换器。与传统的恒定导通时间控制方法需要大输出电容 ESR 以在反馈电压上产生电流斜坡信号以实现稳定运行不同，内部脉冲整形调节器 （PSR） 用于产生等效电感电流斜坡电压。通过将 PSR 和反馈电压的合成信号与参考电压进行比较，当合成信号低于参考电压时，将触发一个导通单触发电路。此外，对于 CCM 中的恒定频率操作，应用锁频环来动态调整导通时间。相反，固定导通时间可以降低轻负载运行期间的开关频率，而较小的开关损耗将提高 DEM 中的轻负载效率。而且，

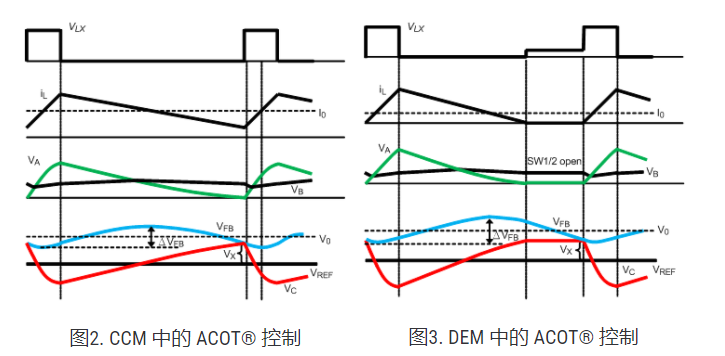
CCM 和 DEM 中 ACOT® 控制回路的运行行为分别如图 2 和图 3 所示。在 CCM 操作中，PSR 电路通过 VA 减去 VB 产生斜坡信号，得到 VC 的信号，其中 VA 和 VB 是内部信号，通过检测开关节点信号。VC 和参考电压的合成信号将用于与闭环控制中的反馈电压进行比较。同时，斜坡纹波的直流偏移可以通过 PSR 的内部采样保持电路适当消除。然而，由于输出电压的波谷控制，输出交流纹波会在输出电压上产生另一个直流偏移。这可能会影响控制精度并限制输出电压的设计裕度。另一方面，在 DEM 操作中，考虑了三种不同的开关导通条件，并在电感电流降至零时保持斜坡电压平坦。这对于 DEM 操作中的稳定回路控制是必不可少的。同样，输出交流纹波将对输出电压产生额外的直流偏移。

 

如前所述，通常添加前馈补偿器以提高噪声容限和瞬态性能。对于图 4 所示的典型前馈补偿器，会生成一个极点和零点以充当高通滤波器，这意味着增益幅度将根据输出信号的不同频率位置而变化。此外，反馈上还有一个额外的相位超前，会影响输出电压上的直流偏移。V OUT到V FB的传递函数可以如式（1）所示，图5中给出了一个更容易实现的例子。A（s）的直流增益等于1 / （1 + R 1 / R 2），并在零频率处增加，然后在极点频率处减小。极点和零点对在反馈信号上提供相位超前，本例的最大相位超前为 51.8˚。在示例波特图中，增益和相位在开关频率下分别为 -13.4dB 和 46.7˚。

 

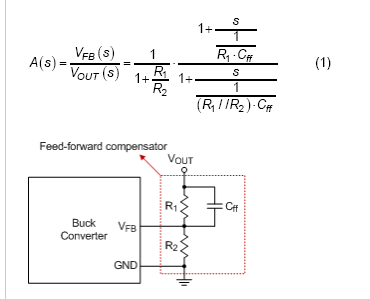
图4. 反馈回路中的前馈补偿器

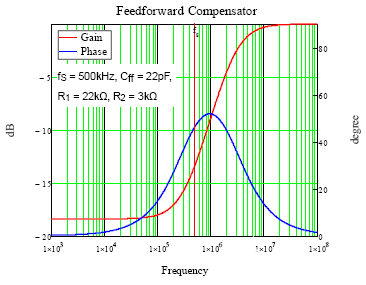
图5. A（s） 的波特图

2. DEM中输出直流偏移的计算

对于具有恒定导通时间控制并在轻负载下工作的降压转换器，当关断时间足够大以释放电感电流时，电感电流可能会达到零。如果电流达到零，则低侧开关将关闭，而高侧开关保持关闭。此时，电感中没有电流流过。然而，高边开关将保持关闭，直到输出电压降低到低于参考电压。在双关状态期间，输出电容器中的剩余电荷由负载电流放电。因此，开关频率将随着 DEM 中的负载电流而变化。开关频率与负载电流的关系可推导出为：

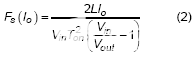
，其中F s是转换器的开关频率，V in是转换器的输入电压，V out是转换器的输出电压，I o是负载电流，T on是高边开关的导通时间。 可以看出，开关频率与输出负载成正比。

由于 DEM 中电感电流的分段线性特性，输出电压纹波由许多不同频率的分量组成。这使得将输出电压纹波视为单一频率信号变得不可行。幸运的是，所有的周期信号都可以分解为各种正弦和余弦函数的组合。鉴于傅里叶变换的线性和时移特性，在考虑前馈补偿器时，将每个分解函数在特定频率处的增益和相位相乘是有意义的。因此，输出电压纹波可以扩展为傅里叶级数。在定义输出电压纹波的稳态方程之前，应先实现电感电流。

在高端开关打开期间，

：

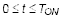
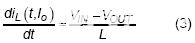
在低边开关打开期间，

：

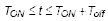
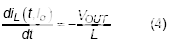
在所有开关关闭期间，

：

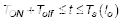
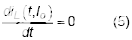
，其中 T s （I o ） 是 I o处的开关周期，T off是低侧开关的开启持续时间。

那么输出电压纹波可以从上面的方程中推导出来，如下所述：

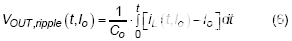
，其中C o是输出电容，需要注意的是，i L和V out，ripple都是时间和I o的函数，开关周期会随着负载电流的变化而变化。需要注意的是，方程（6）中只考虑了交流纹波，直流值在这里并不重要。

下一步，采用傅里叶级数来表示输出电压纹波的函数。以下是具有 N 阶表达式的傅里叶级数的输出电压纹波方程：

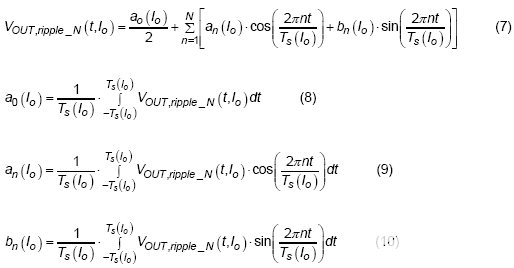
输出电压纹波的函数可以表示为一系列系数不同频率的时间正弦和余弦函数。系数可以通过乘以不同频率的正弦或余弦函数并应用积分来获得平均值。其中a 0 （I o ）是输出负载电流等于Io时的直流分量系数，a n （I o ）是不同负载电流下不同频率的余弦函数系数，b n （I o ） 是不同负载电流下不同频率的正弦函数的系数。

由于定义了输出电压纹波的傅里叶表达式，下一步是使用这些函数作为前馈补偿器 A（s） 的输入。为了更有效地处理时域中两个函数的乘法，然后应用傅里叶变换的卷积特性。卷积特性使得时域中的两个函数可以在频域中相乘。因此，时域反馈信号的描述可以推导出为：

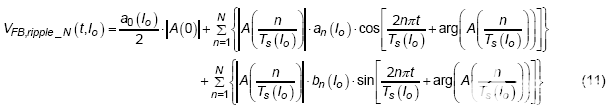
，其中 A（0） 是前馈补偿器的直流增益，| A （n / T s （I o ） ） | 是 （n / T s （I o ） ）特定频率下的增益，arg （ A （n / T s （I o ） ） ） 是 （n / T s （I o ） ）频率下的相移。

由于前馈补偿器和输出电压纹波，会产生额外的直流偏移。为了描述dc offset的值，用一张图来讨论是个不错的方法。如图6所示，有3个信号用来描述这个偏移的来源，第一个是红色实线波形，命名为“Original V FB without phase shift”，它只显示反馈信号的幅度变化但没有相移。在这种情况下，V FB 的纹波电压只会产生部分直流偏移。 对于第二个，红色虚线波形名为“Original V FB with Phase shift”，也考虑了相移，可以注意到V FB低于Vc当触发高边 MOSFET （UG） 的栅极信号时。由于谷底控制机制，最终的V FB in loop 控制将是蓝色实线波形，命名为“V FB with Feed-forward in loop”。可以观察到，已经产生了额外的直流偏移D y 1 。D y 1的公式和反馈电压纹波的平均值可以推导出为：

 

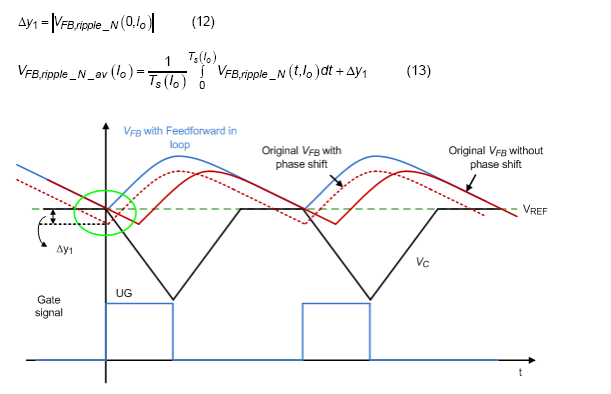
图6 DEM 中反馈信号与内部斜坡信号的关系

3. CCM中输出直流偏置的计算

当转换器在 CCM 下运行时，频率被很好地调节为一个常数。与前面讨论的 DEM 不同，电感电流始终高于零。在稳定运行时，占空比可以由输入和输出电压决定。

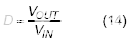
在高端开关打开期间，

：

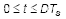
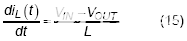
在低边开关打开期间，

：

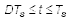
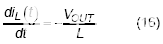
，其中 T s （I o ） 是 I o处的开关周期，T off是低侧开关的开启持续时间。

那么输出电压纹波可以从上面的方程中推导出来，如下所述：

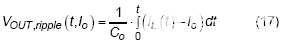
，其中C o是输出电容，I o的直流值不会改变CCM中的开关频率，因此，在下面的推导中只考虑交流纹波。

与 DEM 条件下的分析相同，CCM 输出电压纹波的傅里叶级数也由式 （18）~（21） 推导出来。

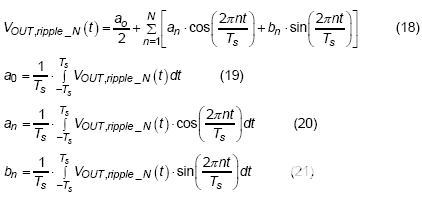
应用卷积特性来处理频域中两个函数的乘法，然后如等式 （22） 那样转移回时域。

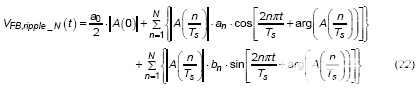
如图 7 所示，三个波形用于描述来自相移的额外直流偏移的来源。与 DEM 部分中描述的故事类似，已生成额外的直流偏移值D y2 并使最终输出电压低于或高于预设值。

 

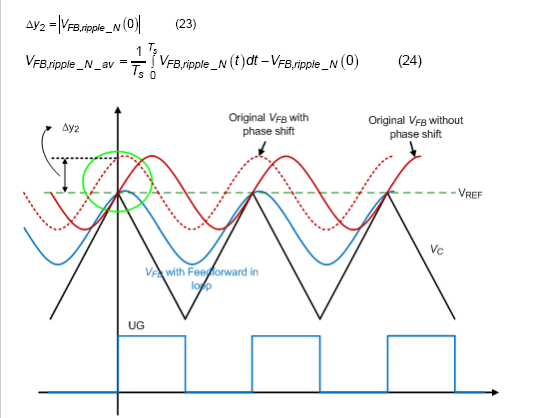
图7. CCM 中反馈信号与内部斜坡信号的关系

4. 通过模拟和实验验证

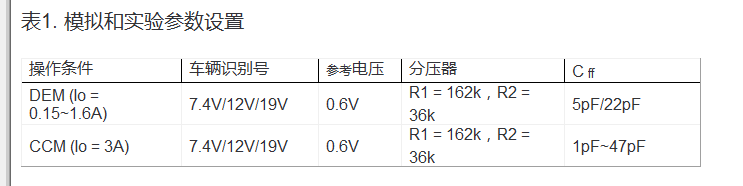
输出直流偏移的起源的详细推导和描述已在前面的章节中给出。这里的主要目的是验证导出公式的准确性。选取一个RT6220 ACOT® 控制转换器的实例来验证计算结果。模拟和实验的详细设置如表 1 所示。结果如图 8 和图 9 所示。它们之间的比较结果将在后面讨论。

（一种）

（二）

（C）

（d）

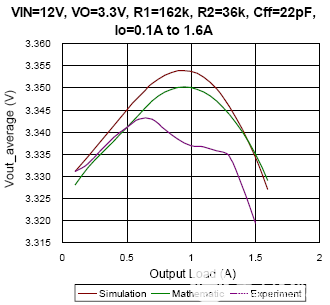
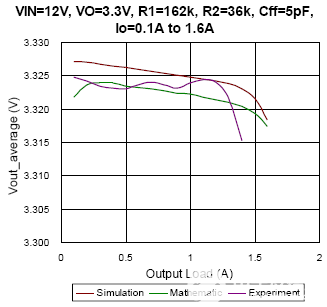
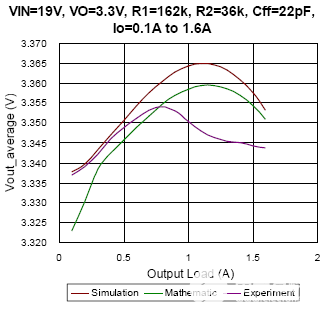
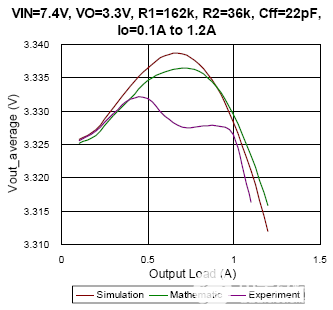
图8 DEM条件下的仿真、数学和实验结果对比

（一种）

（二）

（C）

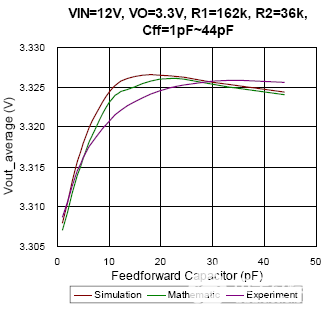
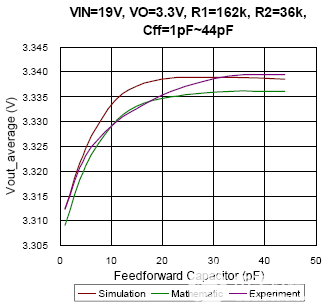
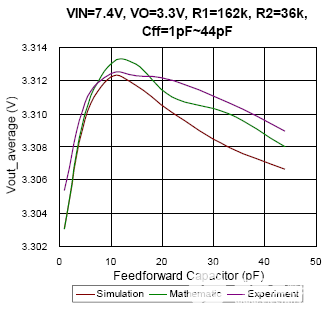
图9 CCM 条件下的仿真、数学和实验结果对比

在图 8 中，描绘了 DEM 下不同输出负载的平均输出电压。从图 8（a） 到图 8（c），转换器设置具有相同的 22pF 前馈电容器，不同的输入电压分别从 7.4V 变为 19V。结果显示，数学结果几乎与模拟结果吻合，偏差小于 0.2%。特别是当占空比接近0.5时，以图8（a）为例，由于输出电压纹波与正弦波形非常相似，数学结果可以很好地估计仿真结果，偏差小于0.07%。然而，在某些条件下，实验结果似乎与模拟和数学结果有很大不同。可能的原因可能是 PCB 布局、噪声干扰、内部 LDO 的调节和寄生元件等。然而，影响实C验中平均输出电压的因素很难在仿真和计算中实现。另一方面，可以观察到前馈电容会影响平均输出电压。比较图 8（c） 与图 8（d），C前一个的ff值为22pF，最大输出电压出现在负载电流为1A而不是空载时，后一个的C ff为5pF，最大输出电压出现在空载时。这表明前馈补偿器在设计中起着重要作用。

图 9 给出了 CCM 中平均输出电压和前馈电容的关系。随着输入电压的变化，输出电压的趋势也会有所不同。也就是说，它不能将一个结果作为每个条件的参考。与 DEM 中的比较结果不同，实验结果与 CCM 中每种条件的模拟和数学结果非常相似。仿真结果与实验结果的最大偏差小于 0.15%。此外，在这个CCM 猜测模型中没有考虑热问题对电压调节的影响，人们可能会误解它与前馈补偿器的原因相同。

5、结论

在应用笔记中，很好地介绍了 CCM 和 DEM 中直流偏移的推导和描述。还给出了一个例子来验证数学结果的准确性，无论是CCM还是DEM，模拟和数学的偏差总是小于0.2%。数学结果的良好预测可以减少设计期间模拟设置的工作量和时间。然而，实际硬件实现的估计仍然存在许多挑战。比如PCB布局、噪声干扰、内部LDO的调节和寄生元件……等等。其中许多不容易预测和建模。毕竟，前馈补偿器产生的额外直流偏移在实际应用中是不可忽视的，通过精确的数学分析可以完成转换器的优化设计。