

一文详解降压转换器的电流纹波系数
描述
电感和电容构成降压转换器中的低通滤波器。LC 滤波器的转角频率始终设计为低频,以衰减开关纹波。根据经验,电感的电流纹波总是设计为平均电感电流的 30% 左右。在本设计说明中,引入了纹波电流与平均电流比(也称为纹波系数)的理论推导,以得到电感器尺寸方程。通过电感器设计的面积积(AP)方法,可以获得纹波因数的最佳范围,这有助于电容器设计以及整个转换器的设计。
介绍
降压转换器广泛应用于许多降压应用,例如板载负载点转换器。基本上,电源开关和续流二极管将直流输入电压斩波为矩形波形,然后低通 LC 滤波器滤除高频开关纹波和噪声,从而在负载端获得几乎纯直流电压。图 1 显示了一个典型的降压转换器。
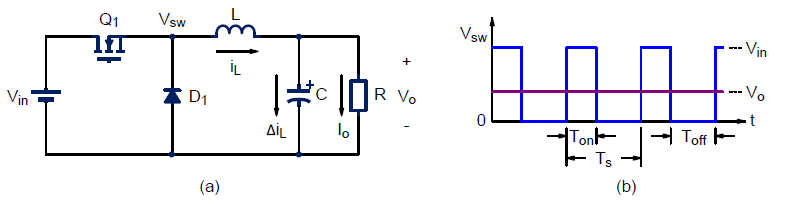
图 1. (a) 典型的降压转换器,(b) 开关电压。
当电源开关Q 1导通时,续流二极管D 1反向偏置。输入电流通过LC滤波器直接加载。当Q 1关断时,D 1被电感电流i L正向偏置。如图 1(b) 所示的开关电压波形是脉动矩形。经过 LC 滤波后,假设 LC 的转折频率远低于开关频率,则输出电压几乎呈现为纯直流。
可以理解,电感L越高,电容C越低导致相同的输出电压纹波。然而,太大的电感器会导致体积大、成本高。而过低的电感会导致输出电容过大。这不仅仅是一个设计权衡问题。让我们考虑一下稳态电感电流的波形。
当功率开关处于导通状态时,电感两端的电压是输入和输出电压之间的电压差。
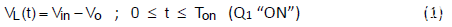
电流将从初始 i L (0) 开始线性增加,

当电源开关处于关断状态时,电感电压与输出电压相同,极性为负极性。
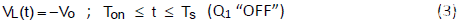
相反,电感电流将从i L (T on ) 以-V o /L 斜率线性减小。
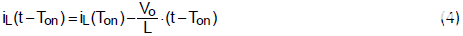
形成电感电压(1)和(3)的伏秒平衡,可以很容易地得到电压传输比,

与图 1(b) 相比,LC 滤波器起到“平均”功能的作用。占空比 D 定义为整个开关周期内的开关开启时间。
纹波系数
图 2 显示了电感电流波形。由于电感的电压波形是脉动矩形,电感电流将呈三角形,具有一定的直流电平。
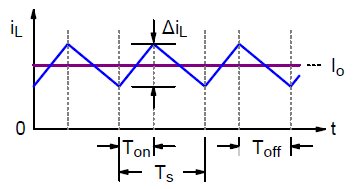
图 2. 电感电流波形
电感的纹波电流定义为

显然,负载电流可以表示为

纹波因子可以定义为

当纹波系数小于 2 时,转换器以连续导通模式 (CCM) 运行,否则以非连续导通模式 (DCM) 运行。在合适的降压转换器设计中,CCM 工作在满载时更为理想,因为它在功率半导体中具有较低的电流应力。因此,本文仅讨论 CCM 操作。
等式 (8) 可以表示为电压相关格式
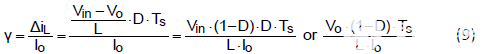
对于固定电感,输入电压越高,纹波系数越高。对于固定的输入电压,电感越小,纹波系数越高。更高的纹波系数意味着更多的纹波电流流过电容器。如果需要相同的纹波电压,则需要更大的电容器。
电感的面积积
如上所述,电感会在开关导通期间储存能量,并在开关关闭时释放能量。从概念上讲,负载电流应通过电感器,因此需要足够面积的绕组线。如果设计较低的纹波系数(或较高的电感),则需要更多的绕组匝数,这导致电感器的尺寸更大。
介绍了一种衡量电感器尺寸的指标——面积积,它是磁芯有效截面积与绕组窗口面积的乘积。单位变为 m 4而不是 m 3体积。然而,面积乘积与核心体积成正比。
根据法拉第定律,电感 (L)、峰值电流 (i pk ) 和磁芯之间的关系可推导出为

其中,i pk = I o + ½ D i L,N 为绕组匝数,B m为磁芯的最大磁通密度。A C是芯的有效横截面积。
从绕组可以得到以下等式。

式中,A wr为绕组导体的截面积,J 为导体的电流密度。k w是磁芯的填充因子,W a是绕组窗口面积。
结合(10)和(11),可以得到

电感器的 RMS 电流可以安排为其直流和交流项。

等式(12)可以重写为
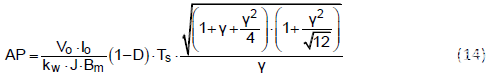
图 3 显示了相对于各种占空比的归一化磁芯尺寸与纹波系数的关系。
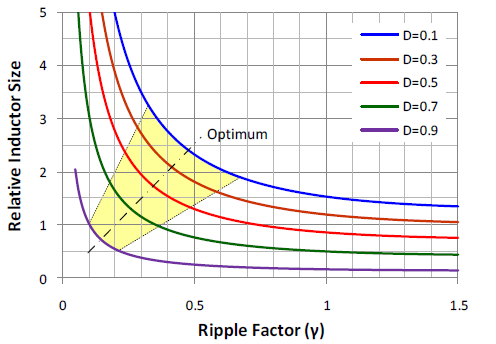
图 3. 纹波系数与电感尺寸与不同占空比的关系。
当纹波因数处于低区域时,磁芯尺寸将显着增加,而在高纹波因数时几乎是平坦的。这意味着在膝盖附近区域存在一个最佳范围。基本上,高纹波系数会导致大滤波电容,反之亦然。例如,当 D = 0.3 时,纹波系数可以设计在 0.2 到 0.4 之间,这会产生适中的磁芯尺寸和适当的电容器尺寸。
设计实例
具有 300kHz 开关频率的降压转换器具有以下工作参数,
V in = 4 ~ 12V, V out = 1.8V, Io = 6A, D V o = 10mV 关于电容。
假设电源开关和续流二极管是理想的。表 1 显示了传统 30% 纹波因数设计的电感,而建议的 AP 方法的最佳计算值如表 2 所示。
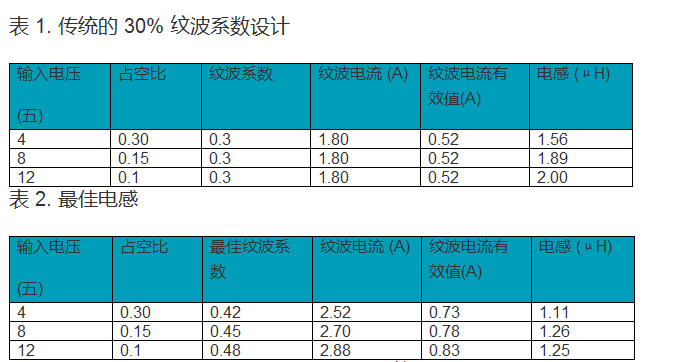
从表 1 可以看出,传统方法具有相同的设计纹波电流,但需要更大的电感器来获得更高的输入电压。而通过应用表 2 中所示的 AP 方法,可以在不同的输入电压下计算出几乎相同的电感。然而,高输入电压的纹波电流较高。在实际的高频设计中,常采用 POCAP 或 MLCC 作为输出电容,其等效串联电阻 (ESR) 极低,很容易满足纹波电压要求。
-
 绝大多数人
2024-03-05
0 回复 举报好文章,马克。 收起回复
绝大多数人
2024-03-05
0 回复 举报好文章,马克。 收起回复
-
低噪声低纹波同步降压转换器模块TPSM8291x的技术解析与应用2025-08-28 686
-
降压型DC-DC转换器与升压型DC-DC转换器的输出纹波差异2024-04-24 2832
-
高效、低噪声和低纹波电流模式同步降压转换器TPS6291x数据表2024-03-08 428
-
使用多相降压转换器和单相转换器的好处2022-11-23 803
-
关于隔离降压转换器的变压器选择讨论!2022-03-11 10053
-
电流模式PWM降压转换器2020-06-19 3763
-
Buck转换器的电流纹波系数2020-03-22 11283
-
反向降压-升压转换器布局方式概述2019-08-12 2436
-
降压、升压和降压升压拓扑结构详解2019-03-19 4212
-
降压转换器的基本工作及不连续模式和续模式2018-11-30 2539
-
使用多相降压转换器的优势2018-11-26 2341
-
如何选择输出段元件最大化DC-DC同步降压转换器性能2018-09-30 1446
-
使用多相位降压转换器有什么好处2018-09-19 1973
-
高轻载效率PSM纹波优化降压型转换器的设计_崔庆2017-01-08 974
全部0条评论

快来发表一下你的评论吧 !

