

点云数据的方位角归一化方法
描述
摘要:点云感知算法是安全鲁棒的自动驾驶系统中尤为重要的一环。在CVPR 2022上,地平线-华中科技大学计算机视觉联合实验室发表了研究成果Azimuth Normalization——以点云特有的径向对称性作为先验,对数据归一化,降低从点云中获取信息的难度。该归一化方法能与大多数感知算法结合,降低对训练数据的需求并提升性能上限,在三维场景感知中有着广泛的应用价值。
简介
从机器学习的角度考虑,数据中隐含的对称性能够作为算法的归纳偏置(inductive bias),对于提升算法精度有很大的帮助。点云是三维场景理解中最重要的表示形式,本工作讨论了点云数据特有的径向对称性(Radial Symmetry),并提出了针对点云数据的方位角归一化方法(Azimuth Normalization / AziNorm)。Azimuth Normalization采用了一种分而治之(Divide-and-conquer)的策略,灵活地分解全场景点云并在子点云上进行归一化。归一化后的子点云具有更简单的模式(pattern),更容易被下游的感知算法识别。Azimuth Normalization具有很强的拓展性,能够应用在多种传感器产生的点云数据上(如LiDAR、RADAR、RGB-D camera),能够与各类感知算法(如检测、分割)结合并且不需要改变具体算法的实现细节和超参数。Azimuth Normalization能够显著提升感知算法的数据效率(Data Efficiency),收敛速度和性能上限,如图1所示,AziNorm与SECOND [1] 检测算法结合提升明显,仅用10%的数据量或迭代次数就优于充分训练的SECOND。
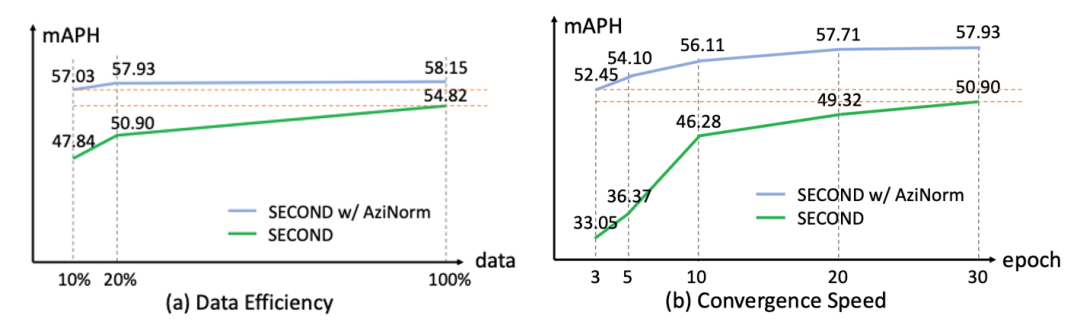
图1 数据效率、收敛速度和性能上限
径向对称性
径向对称性与产生点云数据的传感器(LiDAR / RADAR /RGB-D camera)的工作原理高度相关。以LiDAR为例,如图2,LiDAR始终沿着径向(法向)方向向各个方位角发射电磁波,电磁波触碰到障碍物表面后反射,沿着径向方向反射的回波最终被LiDAR接收,形成点云。因此,产生的点云在径向方向上具有明显的对称性(如图2中,地面的点云对称性明显)。
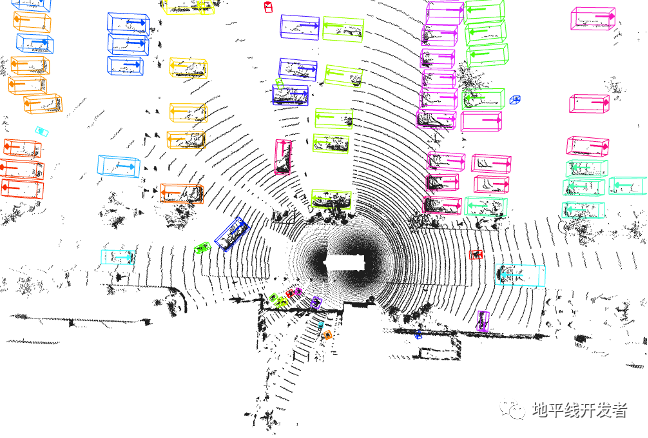
图2 径向对称性(Radial Symmetry)
算法流程
Azimuth Normalization采用了分治的策略,具体流程如下(流程图见图3):
Patch Splitting:把整个感知范围拆分为相互重叠的块(patch), 把全场景的点云规则地分解为子点云;
Patch Filtering:滤除不包含点云的patch、只含地面点的patch(点云具有稀疏性、不均匀性),避免不必要的计算开销;
Normalization:对子点云进行平移变换、旋转变换(对每个点的3D坐标进行),统一各个patch的径向方向;
Patch-wise Perception:在patch level调用现成的感知算法(point-based、voxel-based、hybrid),不需要改变实现细节和超参数;
Inverse Normalization:把感知结果逆变换回原本的LiDAR坐标系;
Patch Merging:融合各个patch结果,对于不同的感知任务可以采用不同的融合策略,例如,对于检测采用非极大值抑制(NMS),对于分割采用逐点平均。
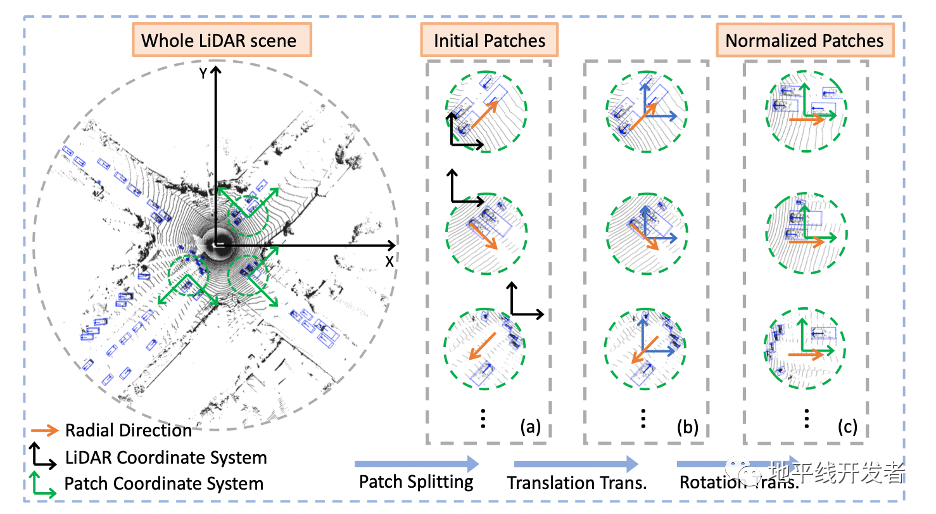
图3 算法流程
实验结果
1. 点云检测和点云分割表1和表2是Azimuth Normalization在点云检测和分割两个感知任务上的实验结果。值得注意的是,对于检测难度大的类别(点稀疏、训练样本数量少),如pedestrian和cyclist,Azimuth Normalization能够带来更明显的增益。Azimuth Normalization极大地简化点云数据中的模式(pattern),消除方位角带来的差异,在归一化后,难类别检测难度显著降低。
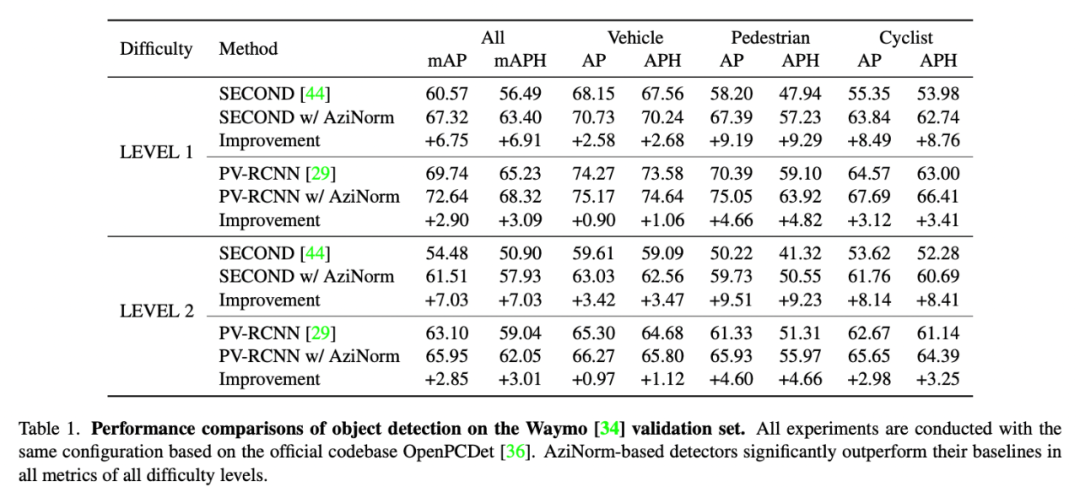
表1 点云检测算法SECOND [1] 和PV-RCNN [2] 在Waymo val set上的实验结果
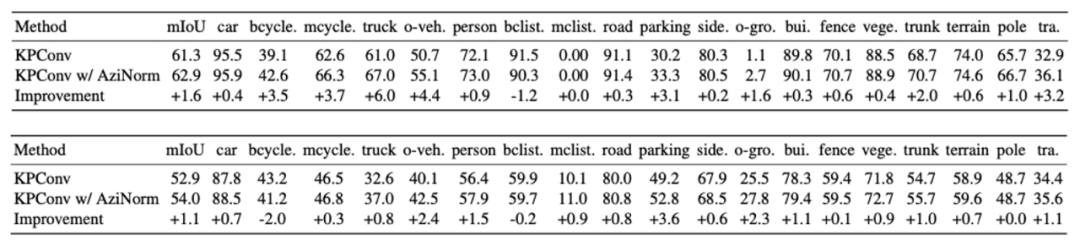
表2 点云分割算法KPConv [3] 在SemanticKitti val set和test set上的实验结果
2. 归一化粒度(Normalization Granularity)图4展示了另一种分治策略,被称之为扇形区域归一化(Sectorial Normalization)。点云被均匀划分为扇形区域,并通过旋转统一径向方向。表3对比了Sectorial Normalization和Azimuth Normalization。4- 和8- Sectorial Normalization 把方位角的变化范围分别缩小到了90º和45º,而Azimuth Normalization的归一化粒度更小,因此性能提升更明显。
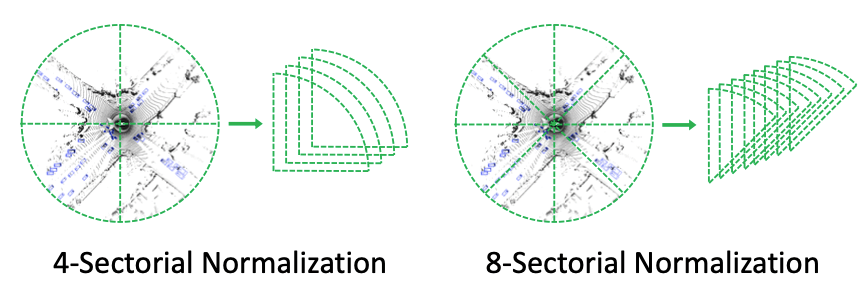
图4 扇形区域归一化(Sectorial Normalization)
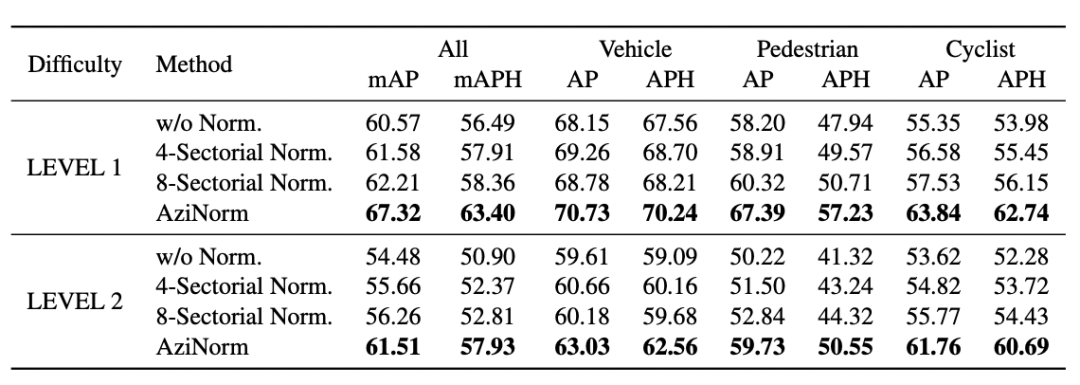
表3 归一化粒度 (Normalization Granularity)
3. 消融实验表4是相关的消融实验,验证了Azimuth Normalization的性能提升主要来自于旋转变换,即对径向方向的归一化,以及Azimuth Normalization对patch的形状layout、尺寸radius、间距stride的选择不敏感。
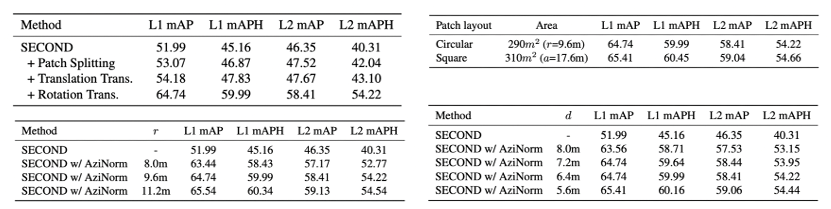
表4 消融实验
总结
Azimuth Normalization利用径向对称性对点云数据进行归一化,带来在数据效率、收敛速度、性能上限三个方面的提升,能够减少感知算法对于数据量的需求,降低标注成本,并且在对感知精度要求高的离线应用场景中有较大的应用价值,如自动标注(Auto Labeling)和生成高精地图(HD Maps)。
原文标题:CVPR 2022 | 基于径向对称性和分治策略的点云方位角归一化
文章出处:【微信公众号:地平线HorizonRobotics】欢迎添加关注!文章转载请注明出处。
审核编辑:汤梓红
-
全国卫星天线仰角、方位角、极化角计算软件软件版2009-10-23 4828
-
项目名“基于FPGA的无线电导航的方位角解调“,刚起步,求大神指点一下?2016-06-10 2984
-
毫米波雷达目标方位角计算2016-11-23 8444
-
发一个计算太阳方位角的软件2017-04-18 9195
-
天线下倾角和方位角调整的网络怎么优化2019-06-12 4672
-
请问谁能帮忙解释下游动方位角?2019-07-29 1862
-
卫星接收天线的方位角计算公式2020-06-01 2632
-
磁力计怎么计算方位角?2023-10-24 696
-
基于C8051F040的方位角测试系统2010-12-24 734
-
陀螺方位角2009-05-04 2266
-
方位角及倾斜角对太阳能电池板发电量的影响2010-09-03 4433
-
一种雷达方位角检测方法2011-05-12 1050
-
自制仰角方位角测试仪,Elevation Azimuth Tester2018-09-20 2150
-
如何提高汽车雷达方位角的分辨率PDF文件讲解2020-11-27 1731
-
如何使用波束实孔径雷达图像提升汽车雷达方位角分辨率的成像方法2020-11-30 1678
全部0条评论

快来发表一下你的评论吧 !

