数据驱动的系统辨识研究

‍‍

 

     我们在上一篇深度学习用于动态系统建模（点击跳转）的文章中针对动态系统的特性与数据驱动的动机进行了论述。我们介绍了动态系统当前输出不仅依赖于当前的输入，还依赖于系统过去的行为（历史输入和历史输出）。我们也介绍了什么场景下使用深度学习/系统辨识来进行系统建模。本文我们主要介绍数据驱动的另一个主题：系统辨识。      为了更好地理解，我们可以设计一个简单的线性系统[链接1]，更具体的是一个连续时间状态空间模型，来解释系统辨识的适用场景：

• 我们创建一个旋转体的状态空间模型，包括转动惯量 J，阻尼力 F 和三个旋转轴:

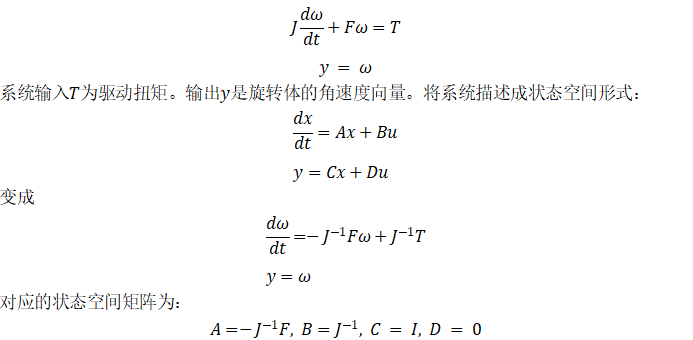
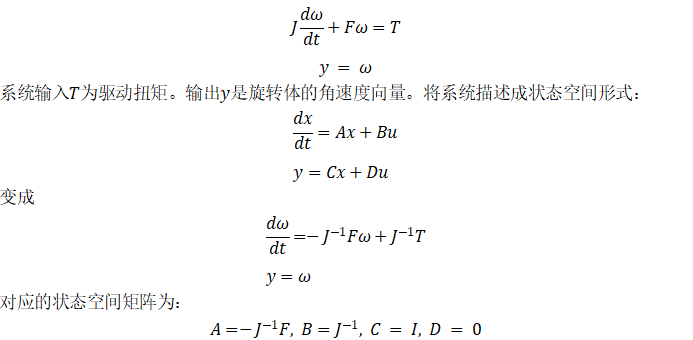系统输入 T 为驱动扭矩。输出 y 是旋转体的角速度向量。将系统描述成状态空间形式：变成

 

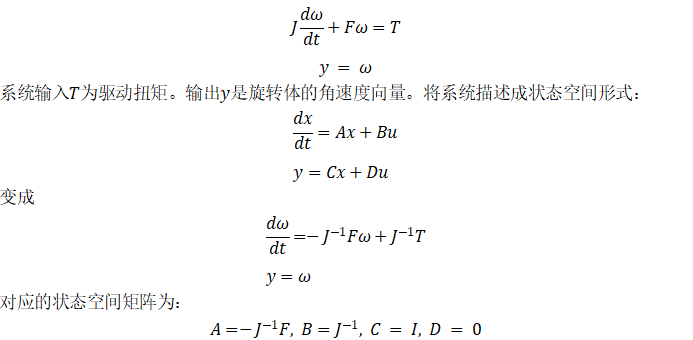
对应的状态空间矩阵为：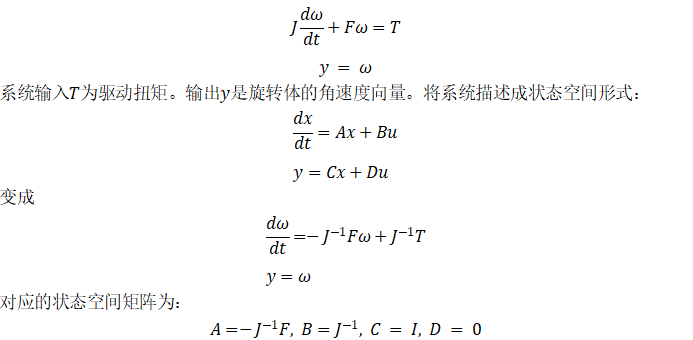

J = [8 -3 -3; -3 8 -3; -3 -3 8];

F = 0.2*eye(3);

A = -JF;

B = inv(J);

C = eye(3);

D = 0;

sys_mimo = ss(A,B,C,D);

 

• 我们随机生成控制输入向量 u 的时间序列，作用于这个系统上，得到系统的输出 y。[链接2]

（滑动窗口查看完整代码）

% 构建随机步长的二值三维序列，N采样数，Nu是控制量的维度

u = idinput([N,Nu],'prbs',frequency,Range);

for i = 1:Nu

% 为二值序列随机赋值，得到不同幅值的序列

    idx = find(diff(u(:,i))) + 1;

    idx = [1;idx];

    for j = 1:length(idx) - 1

    u(idx(j):idx(j+1)-1,i) = randn*u(idx(j));

    end

end

t = (1:N)*dt;

% 将控制输入序列u作用系统上得到系统输出

[y,t] = lsim(sys_mimo,u,t);

输入 u=[u1 u2 u3] 应三个维度的扭矩输入，输出对应 y=[y1 y2 y3] 三个维度的。如下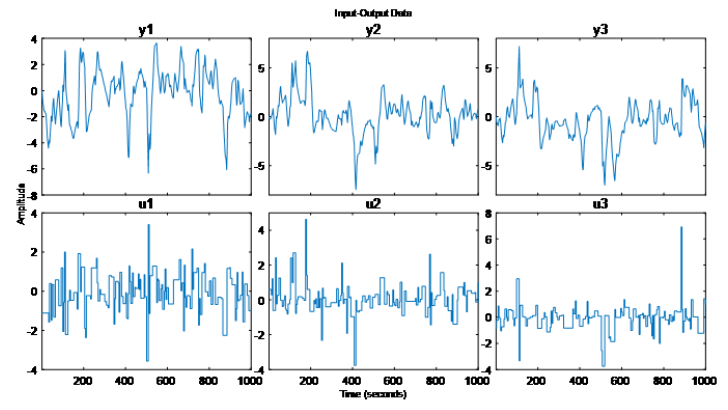：我们现在有系统的输入 u，也有系统的输出 y，这不就是数据科学的菜吗，即使不知道系统模型，是不是也能“拟合”出来 y 和 u 的一个机器学习代理模型 (surrogate model)？我们工程中碰到的动态系统通常也是可以获取系统输入和输出，当然比这个线性系统复杂多了，那能不能也用这种思路得到 y 和 u 的数据模型？接下来，是不是我们只需要把 y 和 u 作为输出（真值）和输入（特征）给到机器学习/深度学习算法，我们就能得到这样一个动态系统的数据模型呢？并非那么简单。原因我们上一篇文章也解释过，动态系统的特殊性，状态在时间维度上是有依赖的，并非某时刻有相同的控制输入就有相同的状态输出，输出也取决于当前系统的状态。我们不妨就用刚才的数据 y 的第一个维度 y1 和 u，直接用几种静态机器学习算法对比动态系统辨识算法来说明这种现象：a) 使用高斯过程回归进行建模[链接3]

 

% 训练回归模型

regressionGP = fitrgp(...

     predictors, ...

     response, ...

     'BasisFunction', 'constant', ...

     'KernelFunction', 'rationalquadratic', ...

     'Standardize', true);

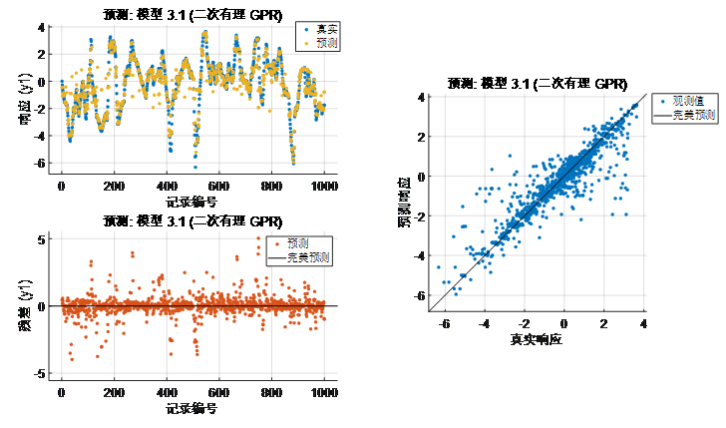图表 1 高斯过程回归 RMSE(Validation):0.7953a) 梯度提升集成回归[链接4]

% 训练回归模型

template = templateTree(...

     'MinLeafSize', 11, ...

     'NumVariablesToSample', 3);

regressionEnsemble = fitrensemble(...

     predictors, ...

     response, ...

     'Method', 'LSBoost', ...

     'NumLearningCycles', 465, ...

     'Learners', template,...

     'LearnRate', 0.2277131533235215);

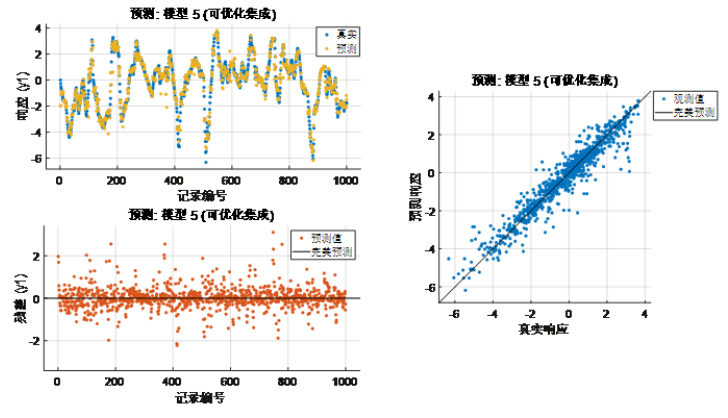图表 2 梯度提升集成 RMSE(Validation):0.5279从上面的高斯过程和梯度提升树表现结果来看，虽然可以捕捉一些系统的特性，尤其梯度提升算法在精度上比高斯过程也有一定的提升，但误差还是较大，系统瞬态特征被“平均”了。上述方式训练的机器学习静态模型，在某瞬时只要输入 u 是相同的，那么输出 y 也是相同的，这与我们提到的动态系统当前时刻的输出不止取决于输入，还依赖于当前系统状态（换句话说即使在某个时刻相同的输入，系统也可以有不同的输出）的特性是不相符合的。当然，可以通过一些特征衍生（例如不同尺度滑窗作用在输入序列上生成新的特征等）的手段得到能够反映状态变化的多尺度特征用于模型训练，这样的方式也使一些统计方法或机器学习模型或前馈神经网络等静态模型可以用于动态系统建模（上篇文章我们也介绍了电池、电机的使用示例）。b) 如果我们换个思路（系统辨识），假使我们提前已经清楚这个系统可以用一个状态空间模型表达，我们直接用动态模型来“拟合”这个动态系统，我们看看效果：nx = 3;sys = ssest(result,nx,'Ts',dt); % 进行状态空间模型系统辨识compare(result,sys) % 查看训练结果其实不必看结果我们也已经估摸到结果可以达到 100% 的准确度，如下图。当然这个例子并非严谨，我们只看了训练过程，也没有准备测试数据，数据本身也没有噪声，但对于说明系统辨识的应用场景还是比较直观的。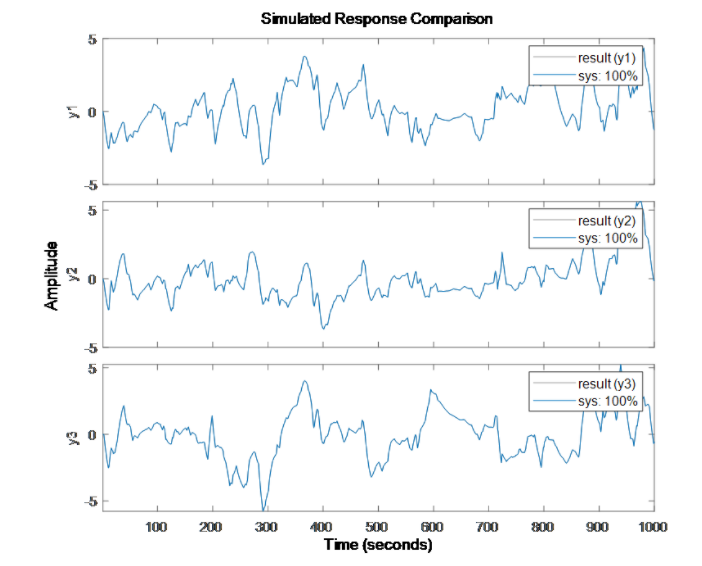

系统辨识利用测量得到的系统输入和输出信号来给那些不容易通过第一原理建模的动态系统构建数学模型。可以通过采集系统的输入 - 输出的时域和频域数据来辨识连续时间或离散时间模型: 包括线性系统辨识，例如传递函数，过程模型，状态空间模型，以及非线性系统动态特性辨识，Hammerstein-Weiner 模型和 NARX（带外部输入的非线性自回归，包含小波网络，树分类，sigmoid 网络等）模型。另外，如果我们对系统结构比较熟悉，也可以利用已有的理论定义含参的模型框架（微分方程），然后通过 Grey-Box 进行模型参数辨识。辨识计算的过程就是模型参数迭代的过程（类似优化算法），方法包括最大似然、预测误差最小化 (PEM) 和子空间系统辨识。最后可以使用辨识好的模型进行响应预测与系统仿真。总结下来整个流程即：接下来我们通过 MATLAB 自带文档示例（[链接5]，示例中提到了数据来源和参考文献^[1]，Dr. Jiandong Wang 和 Dr. Akira Sano）来介绍上述提到的不同的模型。也鼓励大家多多查阅帮助文档。通过该示例，我们展示如何使用阻尼器的速度和阻尼力的测量数据来对系统创建线性、非线性 ARX 和 Hammerstein-Wiener 模型。

示例背景介绍和数据准备

磁流变阻尼器是一种半主动控制装置，用于降低动态结构的振动。磁流变液的粘度取决于输入电压/电流，因此可提供可控的阻尼力。为了研究这个系统的动态性能，将磁流变阻尼器一端固定在地面上，另一端连接到振动台。每 0.005s 采样一次阻尼力 f(t)。每 0.001s 采样一次位移，用于在 0.005s 的采样周期内估计速度 v(t)。系统单输入单输出。输入 v(t) 为阻尼器的速度 [cm/s]，输出为阻尼力 [N]。% F, V, Ts是load mrdamper.mat后加载的数据， 将 F (output force), V (input% velocity) 和 Ts (sample time)封装到iddata对象中.z = iddata(F, V, Ts,'Name', 'MR damper', ...     'InputName', 'v', 'OutputName', 'f',...     'InputUnit', 'cm/s', 'OutputUnit', 'N');  将这个数据集 z 分成两个子集，前 2000 个样本 (ze) 用于估计/训练，其余的 (zv) 用于验证结果。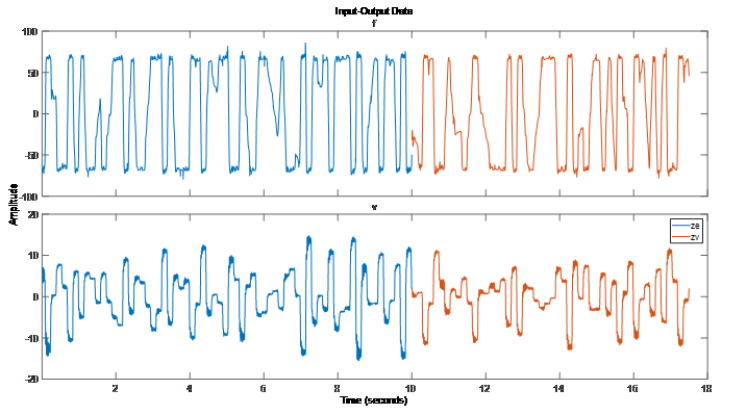

几种线性系统模型

首先尝试从简单的线性模型开始。如果线性模型不能提供令人满意的结果，那它也可以作为探索非线性模型的初值。ARX(Autoregressive with Extra Input) 模型ARX 模型全称带外部输入的自回归 (Autoregressive with Extra Input)。模型结构方程：

模型中 y(t) 是系统 t 时刻的输出，自回归是指模型中含有 y 自身的项 y(t-1)···y(t-na)，na 对应系统极点的个数，也就是 y(t) 和自身的 na 阶有依赖，外部输入项 u(t-nk)+···+(t-nb-nk+1) 是对 y(t) 产生影响的历史输入。其中 nk 是系统的延迟数，也就是 u(t)···u(t-nk+1) 这些项因为系统延迟还不会对 y(t) 产生影响，因此这些项不存在模型中。nb 是系统的零点个数，也就是输入有 nb 阶影响输出。e(t) 是白噪音。模型一种更简洁的写法：

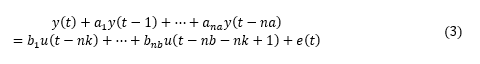
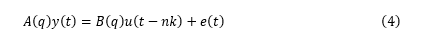
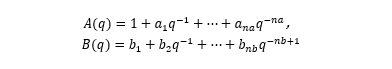其中，q是单位延迟算子，  我们首先利用 ARX 模型来进行模型阶数推荐。阶数的定义取决于模型的类型。通常模型最优阶数是通过试错得到的。但是线性 ARX 模型的阶数可以通过 arxstruc 和 selstruc 等函数自动计算出来。由此得到的阶数也可以作为非线性模型尝试使用的阶数。我们先试着确定线性 ARX 模型的最优阶数。V = arxstruc(ze,zv,struc(1:5, 1:5,1:5));% 尝试让na, nb, nk在[1:5]取值Order = selstruc(V,'aic') % 根据Akaike's Information Criterion 选择阶数Order =     2     4     1AIC 准则选择 Order = [na nb nk]=[2 4 1]，即在选择的 ARX 模型结构中，阻尼力 f(t) 使用 f(t-1)、f(t-2)、v(t-1)、v(t-2)、v(t-3)和v(t-4) 6 个回归量 (regressor) 进行预测。我们先按前面 selstruc 推荐的阶数对应的 ARX 模型进行估计：LinMod1 = arx(ze, [2 4 1]); % ARX 模型 Ay = Bu + e, 形式同上面方程（4）OE 模型

这里先简单介绍一下OE模型,它和传递函数相同，用多项式的比描述系统的输入和输出之间的关系。

模型阶数等于分母多项式的阶数。分母多项式的根称为模型极点。分子多项式的根称为模型零点。传递函数模型的参数是它的极点(阶数 nf)、零点(阶数 nb)和传输延迟(阶数 nk)。离散时间模型形式为:

对应的阶数：

连续时间 OE 或传递函数模型形式为：

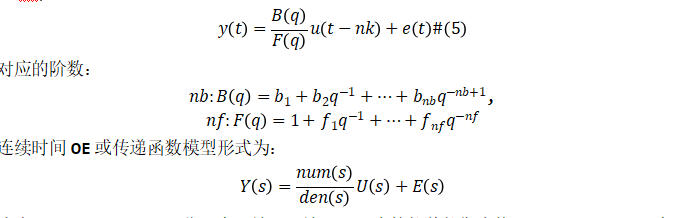
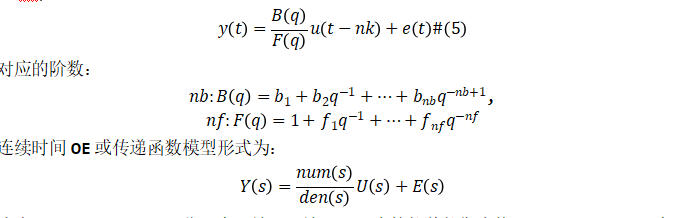
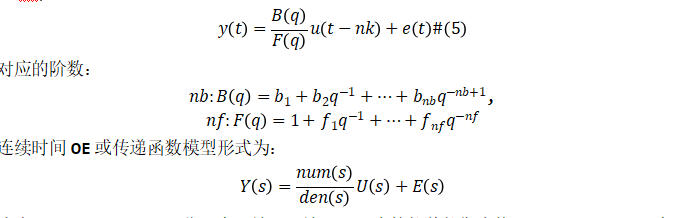
式中，Y(s)、U(s)、E(s) 分别表示输出、输入、噪声的拉普拉斯变换。num(s) 和 den(s) 表示分子和分母多项式，定义了输入和输出之间的关系。

同样我们用上面推荐的阶数进行输出误差模型 (OE) 估计。LinMod2 = oe(ze, [4 2 1]);  % OE 模型 y = B/F u + e，形式同方程（5）

状态空间模型

状态空间模型用一组状态变量的一阶微分（连续时间）或差分（离散时间）方程来描述系统，而不是用一个或多个 n 阶微分或差分方程来描述系统。状态变量 x(t) 可以从测量的输入-输出数据中抽象出来的，但在实验中它们本身不存在或不可测量的。状态方程模型只需要你指定一个输入,即这个模型阶数 n。模型阶数等于 x(t) 的维数，它和对应的线性差分方程中输入输出的延迟数相关,但不一定相等。定义参数化状态空间模型时，连续时间形式通常比离散时间形式容易，因为连续时间就跟你写物理常微分方程类似。连续时间状态空间模型有如下形式:

矩阵 F、G、H 和 D 具有一定的物理意义，例如和材料有关。K 包含扰动矩阵。X0 代表初始状态。可以使用时域和频域数据来估计连续时间状态空间模型。离散时间形式我们就不写了，连续时间频域数据不能用于估计离散时间状态空间模型。回到问题本身，我们可以创建一个线性状态空间模型，其阶数(=状态数)将自动确定:LinMod3 = ssest(ze);% 创建一个 3 阶状态空间模型 state-space model我们可以看一下这三个模型训练集和验证集上效果比较：

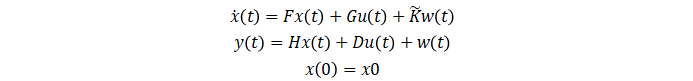
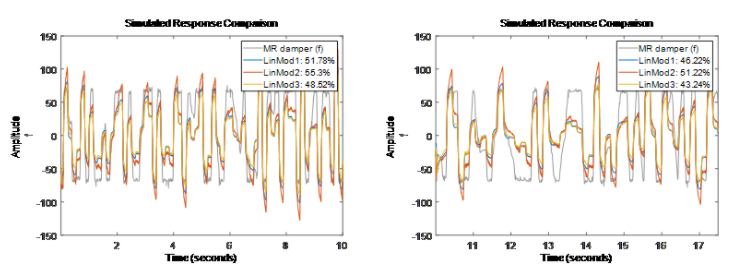
从验证集的结果看最好的模型拟合有 51% 的拟合度（拟合度即 NRMSE 值，100(1-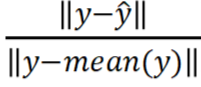），其中 y 是真实值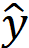， 是模型预测值）。几种非线性系统模型非线性 ARX 模型

前面的尝试看上去线性模型精度还有待提高，我们尝试用 Nonlinear ARX (IDNLARX) 模型。我们也可以用 advice 函数来查看系统的输入输出数据的非线性程度。

advice(ze, 'nonlinearity') % 查看系统的非线性建议There is an indication of nonlinearity in the data.A nonlinear ARX model of order [4 4 1] and idTreePartition function performs better prediction of output than the corresponding ARX model of the same order. Consider using nonlinear models, such as IDNLARX, or IDNLHW. You may also use the "isnlarx" command to test for nonlinearity with more options.非线性 ARX 模型对 ARX 做了一些扩展。它在结构中添加了非线性函数，如小波和 sigmoid 网络，可以模拟复杂的非线性行为。对比线性 ARX 模型，见方程 (3)，我们重新组织一下方程 (3)，把当前输出 y(t) 写成过去输出 + 当前输入 + 过去输入之前权重和的形式, 我们把延迟数 nk 先设置成 0，噪声也不考虑，模型结构简化为：

u(t),y(t),e(t) 分别是输入，输出和噪声。y(t-1),y(t-2),···,y(t-na),u(t),u(t-1),···,u(t-nb-1) 是历史输出和延迟的输入，他们看作 y(t) 的回归量 (regressors,类似机器学习中的特征量，predictors)。系数矩阵 -a₁,···b_nb 是作用在这些回归量上的权重。线性 ARX 的输出 y(t) 是这些回归量的线性权重加和。对比线性 ARX，非线性 ARX 模型：

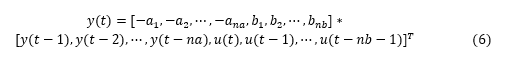
• 与方程 (6) 不同处在于输出 y(t) 与回归量之间的关系不是线性映射，而是一个非线性的映射 F。

F 可以选择不同的非线性函数，如小波网络，多层前馈神经网络，树分类。

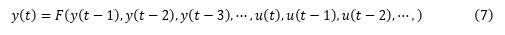
• F 的输入也就是模型的回归量 (regressors)，这些回归量对于线性 ARX 来说都是原始输入和输出的一些延迟项，非线性 ARX 则可以更复杂，可以是各种输入输出的非线性组合，例如：y(t-1)²,y(t-2)*u(t-1),abs(u(t-1)),max(y(t-3)*u(t-1),-10)。

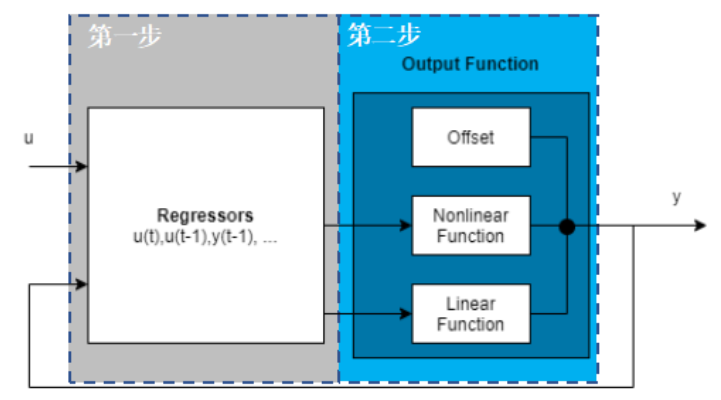我们通过一个结构图更形象的理解非线性 ARX 模型主要通过两步来计算输出有 y(t)1. 根据当前输入 u(t)、历史输入 u(t-1)···、历史输出 y(t-1)··· 计算这些回归量 (regressor) 的值。这些回归量可以认为就是对应机器学习模型的特征量 (predictor)，可以是线性项，例如 u(t-1)，y(t-3),可以是多阶多项式项 u(t-1)²，也可以是一些自定义的变换后的非线性项，例如 u(t-1)*y(t-3)。你可以把这些回归量作为输入指定给模型中的线性函数或者非线性函数。2. 使用输出函数（同时包含线性和非线性两部分）将前面计算的回归量 regressor 映射到输出。例如下面这个函数：

式中 x 对应着回归量（regressor）向量，r 是 x 的均值。L^T(x-r) 输出函数的线性部分，g(Q(x-r)) 代表函数的非线性部分，Q 是一个投影矩。d 是一个补偿偏置。F(x) 可以是任意非线性函数（小波网络，多层感知机网络，树分类网络），当使用数据进行模型辨识时，主要是通过迭代优化来估计模型的参数值，例如 L,r,d,Q 以及网络 g 中的参数。接下来我们回到示例本身，尝试创建非线性 ARX 模型，按我们上面提到的两个步骤，我们首先来创建回归量  (regressor)。简化起见，我们主要使用 linearRegressor 来创建线性回归量，可以通过阶数矩阵 [na nb nk] 来方便创建，至于多阶多项式回归量（可以使用 polynomialRegressor 创建）或者自定义回归量（可以试用 customRegressor 来创建）我们暂不探索。本示例我们主要通过探索不同的模型阶数（上面介绍的阶数矩阵 [na nb nk]）和不同的非线性映射函数（小波、sigmoid 网络、树分类等等）。

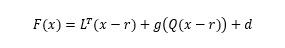
• 估计一个默认的非线性 ARX 模型

 

 

 

 

Options = nlarxOptions('SearchMethod', 'lm'); % 使用 

LevenbergMarquardt 作为估计算法

Options.SearchOptions.MaxIterations = 50;

Narx1 = nlarx(ze, [2 4 1], idSigmoidNetwork,Options)% 模型阶数设置为 [2 4 1]，映射函数选择 sigmoid 网络，这个网络用了一个 sigmoid 函数和一个回归量的线性权重和来计算输出，nlarx 函数用来估计非线性 ARX 模型

disp(Narx1.OutputFcn)

 

Sigmoid NetworkInputs: f(t-1), f(t-2), v(t-1), v(t-2), v(t-3), v(t-4)Output: fNonlinear Function: Sigmoid network with 10 units Linear Function: initialized to [48.3 -3.38 -3.34 -2.7 -1.38 2.15] Output Offset: initialized to -18.9因为阶数 [na nb nk] = [2 4 1],所以模型回归量包含 f(t-1),f(t-2),v(t-1),v(t-2),v(t-3),v(t-4)。此处 f 代表输出，v 代表输入。分别在训练集 ze 和验证集 zv 上进行模型准确度验证。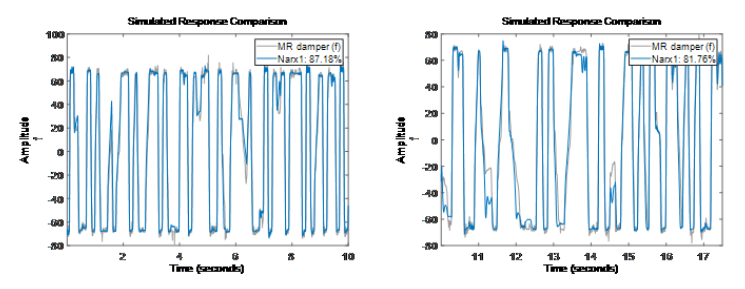通过结果可以看到，同样的阶数情况下，非线性 ARX 比线性模型的结果还是有提升。我们有很多可以尝试的方向来测试不同的模型参数。

• 尝试不同的模型阶数

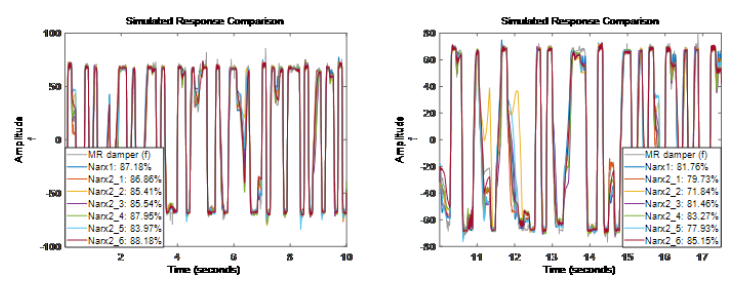图表 3 Narx2 为不同阶数的模型在测试集上的结果从结果看出 Narx2{6} 模型对估计（训练）数据集和验证数据集的拟合结果都很好，同时阶数比 Narx1 的要小。因此，我们将阶数矩阵 [1 3 1] 作为后续试验的阶数，同时将 Nlarx2{6} 作为参考进行拟合比较。阶数矩阵选择对应于使用 [f(t-1)， v(t-1)， v(t-2)， v(t-3)] 作为回归量 (regressor) 集合。

• 尝试修改 Sigmoid 网络函数的隐含单元数

接下来我们尝试修改 Sigmoid 网络函数的隐含单元数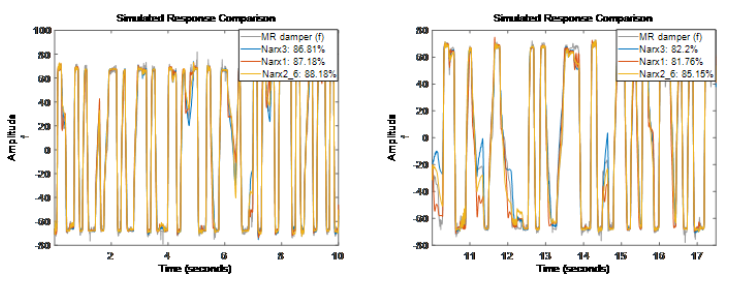。看上去增加隐含单元数并没有带来精度提升 (Narx3结果不如Narx2{6})，所以我们仍然用默认 10 个单元的 Sigmoid 网络。

• 特征选择：给非线性映射函数选择回归量子集

上面的示例中通过阶数矩阵 ([na nb nk] = [1 3 1]) 定义的所有的回归量都会作为非线性映射函数的输入（此处用的 sigmoid 网络）。但当回归量的数量很大时，会增加模型的复杂度。在不改变模型阶数的情况下，可以只选择一部分回归量作为 sigmoid 网络的输入，可以通过 RegressorUsage 来控制特征选择。它的值是一个表，它指定哪些函数使用哪些回归量。例如，我们可以只把输入变量相关的 v(t-1)，v(t-2)，v(t-3) 传给非线性 sigmoid 函数而不需要 f(t-1)这可以通过以下方式实现:Sig = idSigmoidNetwork(10);NarxInit = idnlarx(ze.OutputName, ze.InputName, [1 3 1], Sig);NarxInit.RegressorUsage.("f:NonlinearFcn")(1) = false; % 通过这个指定，回% 归量 v(t-1), v(t-2), and v(t-3) 会被 sigmoid 函数使用，输出回归量 f(t-1) 则不会% 被 sigmoid 函数使用，idSigmoidNetwork 也包含一个线性函数，这个函数则使用了所有% 的回归量disp(NarxInit.RegressorUsage)Narx4 = nlarx(ze, NarxInit, Options);              f:LinearFcn       f:NonlinearFcn              ___________       ______________    f(t-1)       true                   false         v(t-1)       true                   true          v(t-2)       true                   true          v(t-3)       true                   true   创建另一个模型，仅使用回归量 {y1(t-1)， u1(t-2)， u1(t-3)} 作为其非线性分量。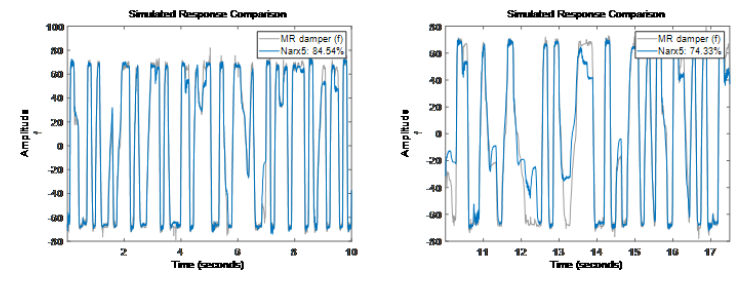Use = false(4,1);Use([1 3 4]) = true;NarxInit.RegressorUsage{:,2} = Use;% 指定 {y1(t-1)， u1(t-2)， u1(t-3)} 作为% 非线性输入量Narx5 = nlarx(ze,NarxInit,Otions);看上去 Narx5 模型在估计数据和验证数据上表现还可以。

• 尝试不同的非线性映射函数

我们这次使用小波网络（对回归量的线性映射和非线性映射两部分中的非线性映射部分使用小波网络）。NarxInit = idnlarx(ze.OutputName, ze.InputName, [1 3 1], idWaveletNetwork);% 仅使用回归量 1 和 3 用于非线性网络映射NarxInit.RegressorUsage.("f:NonlinearFcn")([2 4]) = false;Narx6 = nlarx(ze, NarxInit, Options);除了小波网络，也可以使用树分类非线性函数。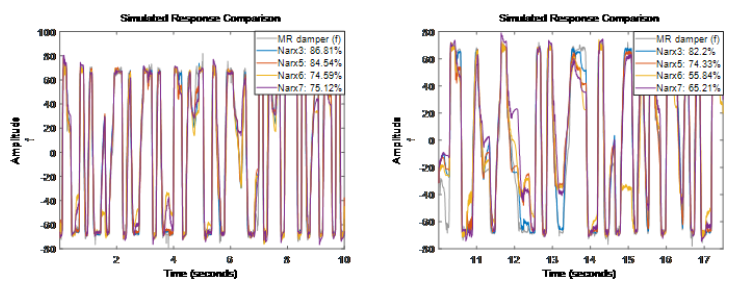TreeNet = idTreePartition;TreeNet.NonlinearFcn.NumberOfUnits = 20;NarxInit.OutputFcn = TreeNet;Narx7 = nlarx(ze, NarxInit, Options);将他们的结果和之前的 Narx3，Narx5 结果进行比较：从目前尝试的结果看 Narx6 和 Narx7 模型的表现比 Narx5 还差一些。

• 分析估计出来的 IDNLARX 模型得到直观解释

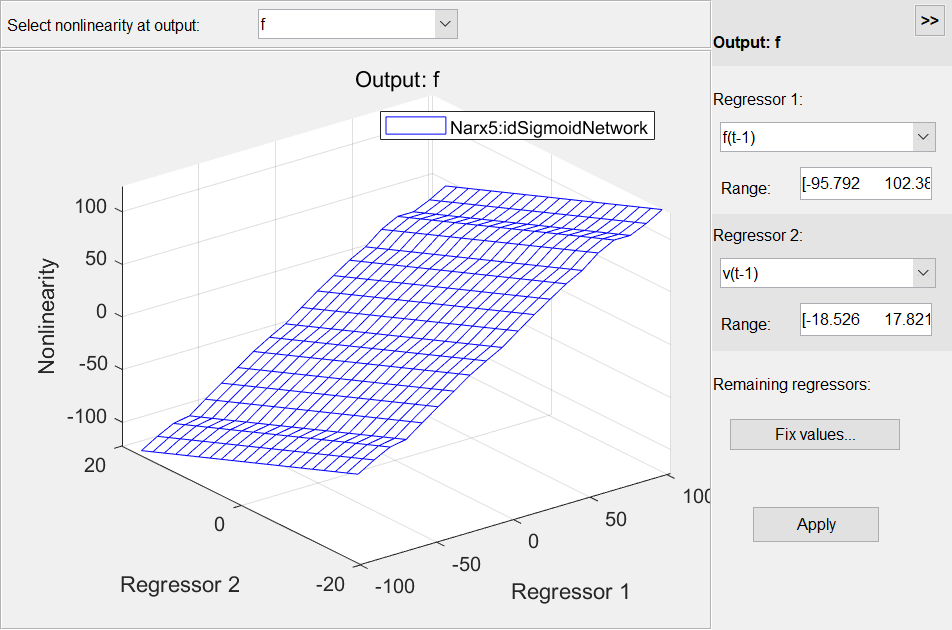我们通过前面的结果选择比较好的模型，接下来可以使用 plot 和 resid 等命令进一步分析来深入了解训练的模型的非线性特性，检查模型 f(t) = F(f(t-1)， F(t-2)， v(t-1)，…，v(t-4)) 中非线性函数 F 的截面。例如，在模型 Narx5 中，函数 F 是一个 sigmoid 网络。为了探究 F() 作为回归量 (regressor) 的函数的形状，可以使用 PLOT 命令:plot(Narx5)plot 函数窗口提供了选择绘制横截面的回归量及其范围的选项。残差检验 (residual test) 可用于进一步模型分析。这个测试用于查看预测误差是否为白噪声且与输入数据不相关。resid(zv, Narx3, Narx5)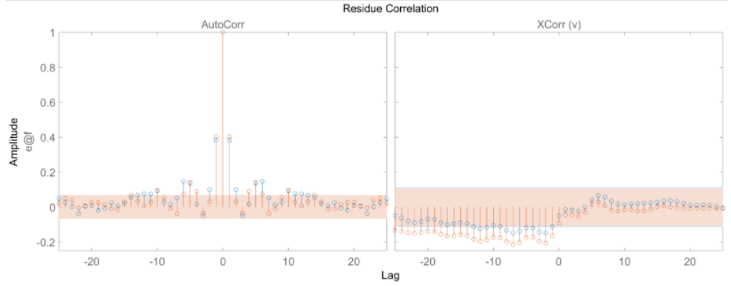残差测试结果失败可能是由于模型没有捕捉到系统的动态。从 Narx3 结果看残差大多在 99% 的置信区间内。非线性 ARX Hammerstein-Wiener模型Hammerstein-Wiener 模型首先是一个非线性模型，但对于动态部分，它其实是一个线性传递函数，那么非线性它怎么实现的?他其实是在输入和输出分别加了一个静态的非线性变换，这样通过一个先行传递函数来描述动态特性再加上输入和输出的两个静态非线性函数，就组成了 Hammerstein-Wiener 模型。图中，f 是一个非线性函数，将输入数据 u(t) 转换（静态变换，t 时刻的输出值只取决于 t 时刻的输入值）为 w(t) = F (u(t))。B/F 是一个线性传递函数，将 w(t) 变换为 x(t) = (B/F)w(t)，这是动态变换。B 和 F 类似于前面介绍的 OE 模型中的多项式。对于 ny 输出和 nu 输入，传递函数矩阵为:

其中，j = 1,2,……,ny和I = 1,2,…,nu 。h 是一个非线性函数，它将 x(t) 的输出映射到(静态变换)系统输出 y(t)，即 y(t) = h (x(t))。我们使用和最开始 OE 模型 LinMod2 相同的阶数 (nb = 4, nf = 2, nk = 1) 来估计一个 IDNLHW(Hammerstein-Wiener) 模型。使用 sigmoid 网络作为 HW 模型非线性输入和输出。nlhw函数和其他估计函数（如 oe, nlarx 等函数）一样。Opt = nlhwOptions('SearchMethod','lm');UNL = idSigmoidNetwork;YNL = idSigmoidNetwork;Nhw1 = nlhw(ze, [4 2 1], UNL, YNL, Opt)Nhw1 =Hammerstein-Wiener model with 1 output and 1 input Linear transfer function corresponding to the orders nb = 4, nf = 2, nk = 1 Input nonlinearity: Sigmoid network with 10 units Output nonlinearity: Sigmoid network with 10 unitsSample time: 0.005 secondsnhw1 模型在验证数据上有约 70% 的拟合度。

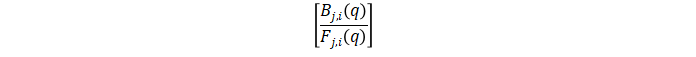
• 分析估计的 IDNLHW 模型

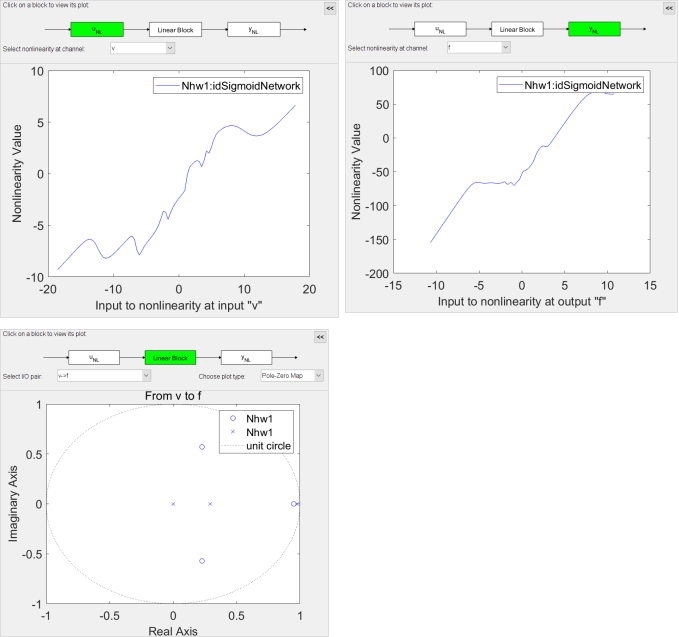和非线性 ARX 模型类似，Hammerstein-Wiener 模型也可以使用 PLOT 命令检查 I/O 非线性和中间部分线性传函的特性。plot(Nhw1)从结果可以看出输入非线性函数（像一个饱和函数）和输出非线性函数（像一个分段线性函数）的形状。线性传函模块的零极点图中有一个零点和一个极点非常接近，说明可以去掉它们，从而减少模型的阶数。接下来和 IDNLARX 一样我们可以尝试不同的模型参数，包括阶数和输入输出的非线性函数。此处不在赘述，大家可以根据示例自由尝试。

Conclusions 总结

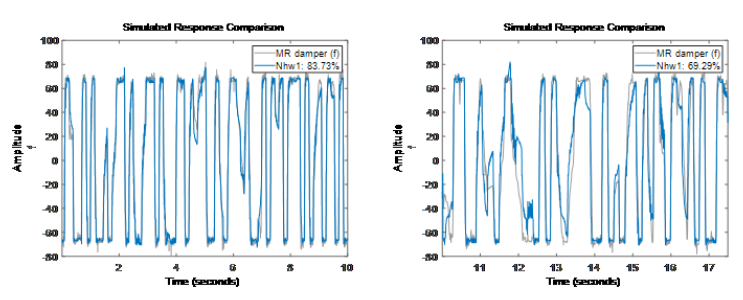
我们探索了各种非线性模型来表达输入电压和输出阻尼力之间的动态关系。结果表明，在非线性 ARX 模型中，Narx2{6} 和 Narx5 表现最好，而在 Hammerstein-Wiener 模型中，Nhw1 表现最好。非线性ARX模型最好的描述了 MR 阻尼器的动态特性 (拟合度最好)。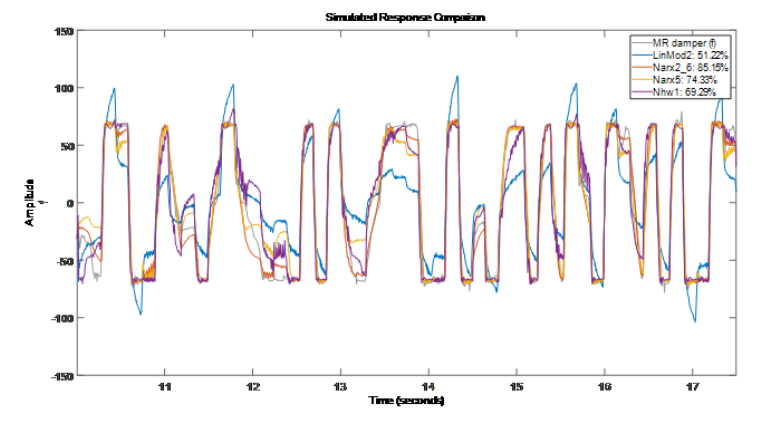通过示例我们看到每种模型类型都有多个可用调项。例如对于非线性 ARX 模型，我们不仅可以指定模型的阶数和非线性函数的类型，还可以修改和设置回归量以及调整对应函数的属性。对于 Hammerstein-Wiener 模型，我们可以选择输入输出非线性函数的类型，以及线性传函的阶数。因此使用数据辨识模型可以在对模型结构或动力学缺乏明确原理的情况下，尝试各种选项，并分析它们对结果模型质量的影响。当然这个示例本身是单输入单输出（SISO，Single Input Single Output）的系统, 对于多输入多输出（MIMO, Multi-Input Multi-Output）的系统上述大部分模型也都支持。具体的MIMO也可以查看文档中更多的示例[链接6]。  

附言：

系统辨识还有很多内容文中示例没有涉及，例如 Grey-Box 模型估计，在线估计。附言中简单介绍一下，也欢迎查阅相关详细链接。

Grey-Box 模型

对于 Grey-Box 模型估计[链接7]，总体思想是说你已经有了系统的微分/差分方程（线性，非线性）、状态空间方程等等，但方程的系数是未知的，可以使用数据进行方程系数的估计。这种估计的难点通产是构建这个含参数的线性或非线性的系统方程。可以参考示例：包括车辆模型、电机模型、飞行器模型等等。

在线估计

在线估计[链接8]顾名思义就是说在物理系统（被控对象）运行过程中，利用实时流数据不断地对模型的参数和状态进行估计。

• 针对在线参数估计，主要使用迭代算法，利用当前的实时测量数据和历史的参数估计值来估计当前模型（文章前面提到的模型）的参数值，算法迭代效率比较高，也可以支持嵌入式。
• 针对在线状态估计，主要包含几种状态估计器，Kalman Filter（线性系统），Extended Kalman Filter（可线性化的非线性系统），Unscented Kalman Filter（非线性系统）， Particle Filter （类似 UKF）等。

 

原文标题：数据驱动的动态系统（Dynamical System）建模(二)：系统辨识

文章出处：【微信公众号：MATLAB】欢迎添加关注！文章转载请注明出处。

审核编辑：汤梓红