

什么是谐波畸变
描述
谐波畸变是由电力系统中的非线性设备引起的。非线性器件是指电流与施加的电压不成比例的器件。图1通过将正弦电压施加于简单非线性电阻的情况说明了这一概念,其中电压和电流根据所示曲线变化。虽然施加的电压是完美的正弦曲线,但产生的电流是失真的。
将电压提高几个百分点可能会使电流加倍,并呈现不同的波形。这是电力系统中大多数谐波失真的来源。
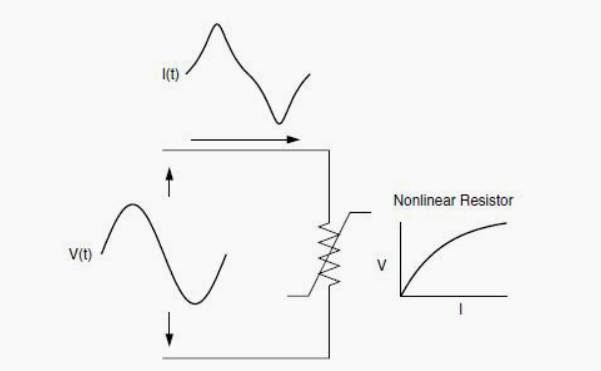
图1非线性电阻引起的电流失真。
图2说明任何周期性的失真波形都可以表示为正弦曲线的总和。当一个波形从一个周期到下一个周期都相同时,它可以表示为正弦波其中每个正弦波的频率是失真波基频的整数倍。这个倍数被称为基波的谐波,因此这个主题的名称。
正弦曲线的总和被称为a傅里叶级数,以发现这一概念的伟大数学家命名。
由于上述性质,傅立叶级数概念被普遍应用于分析调和问题。现在可以在每个谐波下单独分析系统。此外,与整个失真波形相比,单独找出每个谐波的正弦曲线的系统响应要简单得多。每个频率的输出然后被组合以形成新的傅里叶级数如果需要的话,可以从中计算出输出波形。
通常,我们只关心谐波的幅度。当波形的正负半周形状相同时,傅立叶级数只包含奇次谐波。这为大多数电力系统研究提供了进一步的简化,因为大多数常见的谐波产生设备在两种极性下看起来都是一样的。事实上,偶次谐波的存在通常是一个线索,表明负载设备或用于测量的传感器有问题。
也有明显的例外,如半波整流器和电弧炉,这时电弧是随机的。
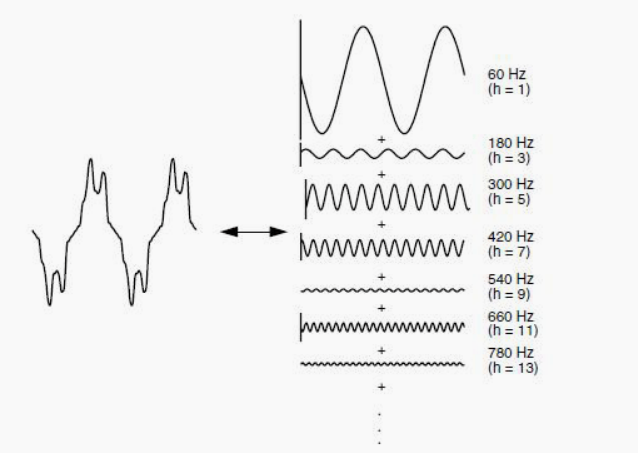
图2失真波形的傅立叶级数表示
通常,在电力系统分析中,高阶谐波(高于25次至50次的范围,取决于系统)可以忽略不计。
虽然它们可能会干扰低功率电子设备,但通常不会损坏电力系统。在这些频率下,也很难收集足够精确的数据来模拟电力系统。一个常见的例外是在频率范围内存在系统共振。这些谐振可以由电子功率转换器中的陷波或开关瞬态激发。这会导致电压波形出现多个过零点,从而干扰定时电路。这些谐振通常发生在有地下电缆但没有功率因数校正电容器的系统上。
如果按照惯例将电力系统描述为串联和并联元件,则系统中的绝大部分非线性存在于并联元件(即LOD)中。电力输送系统的串联阻抗(即电源和负载之间的短路阻抗)是非常线性的。在变压器中,谐波源也是普通“T”模型的并联支路(磁化阻抗);泄漏阻抗是线性的。
因此,谐波失真的主要来源最终将是最终用户负载。这并不是说所有经历谐波失真的最终用户本身都有很大的谐波源,而是说谐波失真通常源于某些最终用户的负载或负载组合。
-
什么是谐波畸变?谐波通俗点怎么理解?2023-09-21 2838
-
如何改善逆变器谐波畸变?2023-09-15 4607
-
AD8231程控增益仪表放大器谐波畸变2018-10-11 2308
-
电流谐波畸变率标准2017-10-26 42164
全部0条评论

快来发表一下你的评论吧 !

