

积分增益的含义及计算方法
描述
本文讨论了积分增益的含义以及如何计算积分增益以获得更好的控制效果。
一些控制系统可以依靠比例系统的简单数学来实现所需的结果。然而,再多的比例增益也无法通过即时响应产生完美——事实上,现实世界中没有任何系统可以做到这一点。但是,如果要实现更好的控制量,通常需要积分增益来带来更好的结果。
积分增益的含义
大多数控制系统使用某种反馈来为过程提供可变输出信号。这些输出是使用各种耦合在一起的术语仔细计算的,以便为液压阀、加热器、电机控制器和任何其他需要比简单的开/关控制更精确的设备提供输出电压。
计算这个输出信号是依赖于系统中的误差量的几个数学项的综合努力。如许多文本中所述,误差是预期系统目标值 (SetPoint SP) 与来自过程的当前感测值 (过程变量 PV) 之间的差异。
错误=SP-PV
此输出计算器中使用的最基本术语使用称为比例增益的乘法常数,它是误差与输出信号的直接比率。一个小错误表示接近目标,因此输出信号开始趋于平稳。否则,系统将全速行驶,直到射过目标并需要返回。这个概念被恰当地称为“过冲”。
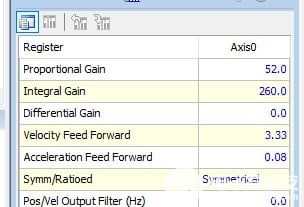
带有包括积分增益在内的参数的调谐输出显示示例。很多时候,软件通过内置算法进行调整,而其他时候,则需要手动计算增益值。
在使用增加的比例增益 (Kp) 来提供稳定性的比例控制系统中存在两个主要弱点。首先,输出达到最终稳定值的速度较慢,并且最终稳定值可能无法达到目标,从而提供稳态误差。
解决此问题的一种方法是添加积分增益 (Ki) 的第二个常用项,它可以在一定程度上抵消这些影响,但确实提供了其自身的弱点,必须在 Kp 效应旁边加以平衡。
计算积分增益
积分过程是一个微积分概念,但实际情况是它不需要数学背景来理解所使用的方法。从技术上讲,积分是方程定义的曲线下方或曲线之间的面积的连续添加。不同之处在于,对于现实世界的系统,整个目的是补偿影响操作的外部变化。
如果系统在 100% 的情况下是完全可预测和可计算的,则没有理由进行反馈和控制输出的连续轻微变化。实际上,每次系统运行时,SP 和 PV 之间的误差差异都会发生变化,因此基于平滑的方程驱动曲线的计算是行不通的。
即使它可能不符合可预测的数学曲线,积分项仍然使用这种不断增加或“求和”的误差。可能如下图所示:
积分项=Kiotimeerrord(error)
尽管这是正确的表示法,但它对实际系统意义不大。实际上,该过程看起来更像这样:
积分项=Ki(error1+error2+error3.。.+errorN)
如您所见,随着时间的推移误差越大,积分项的贡献越大。Ki 只是一个无单位的乘数,其范围可能从小十进制值到较大的值,具体取决于系统的大小。误差可能在硬盘驱动针运动的几分之一毫米的大小上,或者可能是液压缸位置的大量英寸,因此没有单一的增益值可以应用于每个系统。
积分增益的影响
误差的累积需要时间,因此当进入系统 SP 时,不会立即看到积分增益 (Ki) 的结果。在那一刻,错误开始产生。
一旦有轻微的误差累积,较大的 Ki 值将导致系统更快地达到设定点。如果系统在达到设定点之前由于较大的比例增益因子而开始趋于平稳,这将特别有用。在这种情况下,误差将开始攀升,但速度是一致的。
Ki 值较高的问题是在系统响应错误时重新引入过冲,即使接近 SP。
从视觉上看,只有 Ki 的系统的效果在开始时会表现为一个未补偿的系统(就像它完全没有增益一样)。变化率在短时间内是相当线性的。很快,随着错误的增加,系统的变化率会增加,加速向 SP。过冲肯定会在系统稳定之前出现。
一个主要的好处是,即使有振荡,系统最终也会稳定在目标 SP,因为即使是一点点稳态误差最终也会导致输出上升,足以达到 SP。
在累积输出的一种特殊情况下,如果系统无法物理到达 SP,例如温度控制系统冷却过快而无法达到目标 SP,那么误差将继续攀升。该系统将不断尝试将加热元件驱动得越来越高,超出其物理极限,例如,发送 15 伏的电压来控制只能接受高达 10 伏的电压。
到了冷却时间,加热器控制输出会降低,但电压控制下降到 10 伏需要一些时间,最后,系统才会真正响应。这称为“积分饱和”或“复位饱和”,如果满足此条件,则必须从方程中补偿。
由于产量的快速增长,很少能单独看到一个积分系统。它们将始终与比例项(PI 系统)或第三个附加微分项(PID 系统)配对。
-
阻抗计算方法2013-06-10 3183
-
机器视觉计算方法2015-08-14 7908
-
处理增益的计算方法是什么?2021-06-01 4911
-
Rstart的计算方法2021-10-29 2039
-
对电流进行积分用何种计算方法?2023-11-01 829
-
IFFT的计算方法2008-10-30 14173
-
甲类单端的简易计算方法2016-01-19 1081
-
特征阻抗的计算方法2017-06-09 3027
-
电磁场数值计算方法及电磁铁的设计2017-11-20 2247
-
任意重积分自适应递归式快速计算方法2021-04-16 922
-
一种任意重积分自适应递归式快速计算方法2021-05-10 647
-
EMC计算方法和EMC仿真(1) 计算方法简介2023-02-14 4396
-
工信部:新能源乘用车标准车型分值平均降低40%,调整双积分计算方法2023-07-07 1246
-
EMC计算方法和EMC仿真(1) ——计算方法简介2023-12-05 2817
-
【SOC的多种计算方法】2024-06-05 5144
全部0条评论

快来发表一下你的评论吧 !

