

常用锐化算法及Sobel锐化的介绍
描述
1. 图像锐化原理介绍
在增强图像之前一般会先对图像进行平滑处理以减少或消除噪声。图像的能量主要集中在低频部分,而噪声和图像边缘信息的能量主要集中在高频部分。因此,平滑处理会使原始图像的边缘和轮廓变得模糊。为了减少这类不利效果的影响,需要利用图像锐化技术,使图像的边缘变得清晰。图像锐化处理主要有两个目的:一是与图像平滑处理相反,增强图像边缘,使模糊的图像更加清晰,颜色变得鲜明突出,图像的质量有所改善,产生更适合人观察和识别的图像;二是经过锐化处理后,目标物体的边缘鲜明,以便于计算机提取目标物体的边界、对图像进行分割、目标区域识别、区域形状提取等,为图像理解和分析打下基础。 经过平滑处理的图像变得模糊的根本原因是因为图像受到了平均或积分运算,因此可以对其进行逆运算(如微分运算)就可以使图像变得清晰。微分运算是求信号的变化率,由傅立叶变换的微分性质可知,微分运算具有加强高频分量的作用。但需要注意的是,进行锐化处理的图像必须有较高的性噪比,否则锐化后图像性噪比反而更低,从而使得噪声增加的比信号还要多,因此一般是先消除或减轻噪声后再进行锐化处理,如图1所示。

图1 图像锐化示意图
物体的边缘是以图像局部特性不连续性的形式出现的,即边缘意味着一个区域的结束和另一个区域的开始。图像边缘有方向和幅度两个参数。通常,沿边缘走向的像素变化平缓,而垂直于边缘走向的像素变化剧烈。边缘一般有两类(图2所示):(1)阶跃状边缘,它两边的像素灰度值显著不同;(2)屋顶状边缘,它位于像素灰度值从增加到减少(或从减少到增加)的变化转折点。经典的边缘提取方法是考虑图像的每个像素在某个领域内的变化,利用边缘邻近一阶或二阶方向导数变化规律来检测边缘。图像灰度值的显著变化可以用一阶差分替代一阶微分的梯度来表示,分别以梯度向量的幅度和方向来表示。因此,图像中陡峭边缘的梯度值很大;灰度值变化平缓的地方,梯度值较小;灰度值相同的地方,梯度值为零。
下面开始介绍运用一阶微分和二阶微分运算来进行图像边缘检测的原理。
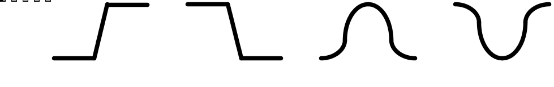
图2 边缘类型
1.1.一阶微分边缘检测
一阶微分主要是指梯度模运算,图像的梯度模值包含了边界及细节信息。图像
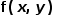 在点
在点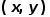 处的梯度定义为:
处的梯度定义为: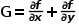 由于数字图像是离散的,所以可以用差分来替代微分,即:
由于数字图像是离散的,所以可以用差分来替代微分,即: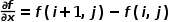
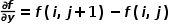 梯度的幅值即模值,为:
梯度的幅值即模值,为: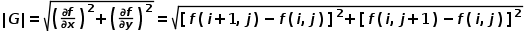 梯度的方向为:
梯度的方向为: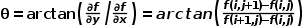 对图像f使用梯度模算子进行运算后,可产生一幅梯度图像g,图像g和图像f之间的像素关系为:
对图像f使用梯度模算子进行运算后,可产生一幅梯度图像g,图像g和图像f之间的像素关系为: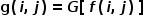 其中G为梯度模算子。由于梯度图像g反映了图像f的灰度变化分布信息,因此可以对其进行某种适当的处理和变换,或将变换后的梯度图像和原图像组合作为f锐化后的图像。运用一阶微分运算的边缘检测算子包括Robert算子、Prewitt算子和Sobel算子等等,将在后续小节中对Robert和Sobel边缘检测算法的实现进行介绍。
其中G为梯度模算子。由于梯度图像g反映了图像f的灰度变化分布信息,因此可以对其进行某种适当的处理和变换,或将变换后的梯度图像和原图像组合作为f锐化后的图像。运用一阶微分运算的边缘检测算子包括Robert算子、Prewitt算子和Sobel算子等等,将在后续小节中对Robert和Sobel边缘检测算法的实现进行介绍。
1.2.二阶微分边缘检测
二阶微分定义为
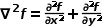 。考虑坐标旋转变换,设P点旋转前坐标为
。考虑坐标旋转变换,设P点旋转前坐标为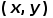 ,顺时针旋转θ°后得
,顺时针旋转θ°后得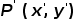 ,如图3所示,则有:
,如图3所示,则有:
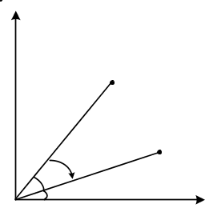 图3 坐标旋转变换
图3 坐标旋转变换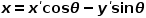
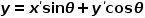
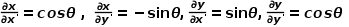 函数
函数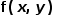 对
对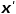 的一阶偏导数为
的一阶偏导数为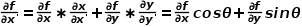 函数
函数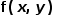 对
对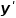 的一阶偏导数为
的一阶偏导数为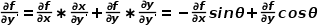 函数
函数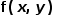 对
对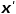 的二阶偏导数为
的二阶偏导数为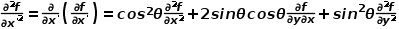 函数
函数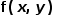 对
对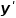 的二阶偏导数为
的二阶偏导数为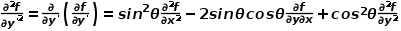 将函数
将函数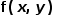 对
对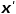 和
和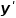 的二阶偏导数相加得
的二阶偏导数相加得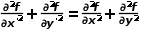 由此可见,二阶微分具有各向同性、旋转不变性的特征,从而满足不同走向的图像边缘的锐化要求。
由于数字图像是离散的,所以可以用差分来替代微分,即:
由此可见,二阶微分具有各向同性、旋转不变性的特征,从而满足不同走向的图像边缘的锐化要求。
由于数字图像是离散的,所以可以用差分来替代微分,即:
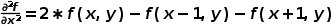
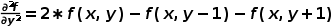
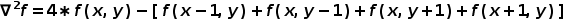 后续小节将要介绍的Laplacian边缘检测算法正是基于二阶微分运算。
后续小节将要介绍的Laplacian边缘检测算法正是基于二阶微分运算。
1.3.一阶微分与二阶微分边缘检测对比
一阶微分和二阶微分运算都可以用来检测图像边缘,但它们对边缘的检测原理和检测效果是有差异的,如下所示: (1)对于突变型的细节,通过一阶微分的极值点和二阶微分的过零点均可以检测出来,如图4所示。
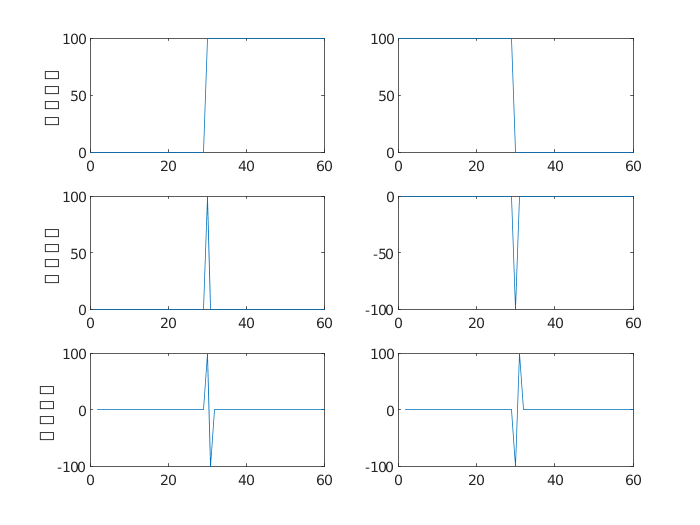
图4 突变型细节
(2)对于细线型的细节,通过一阶微分的过零点和二阶微分的极值点均可以检测出来,如图5所示。
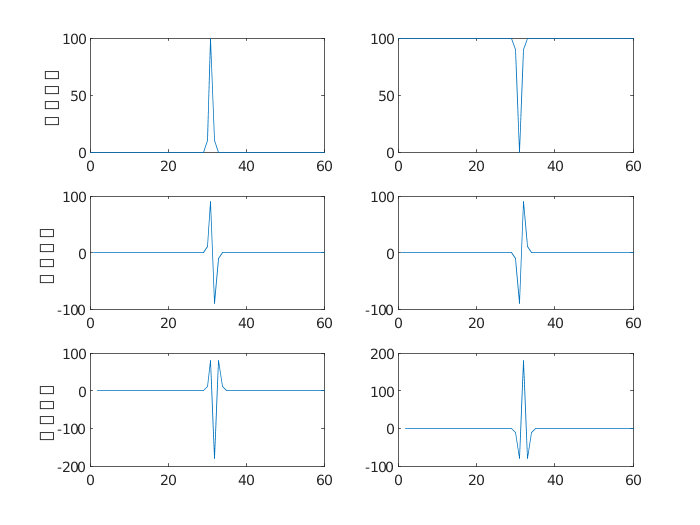
图5 细线型细节
(3)对于渐变型的细节,一般情况下突变幅度小、定位难、不易检测,但二阶微分的信息比一阶微分的信息多,如图6所示。
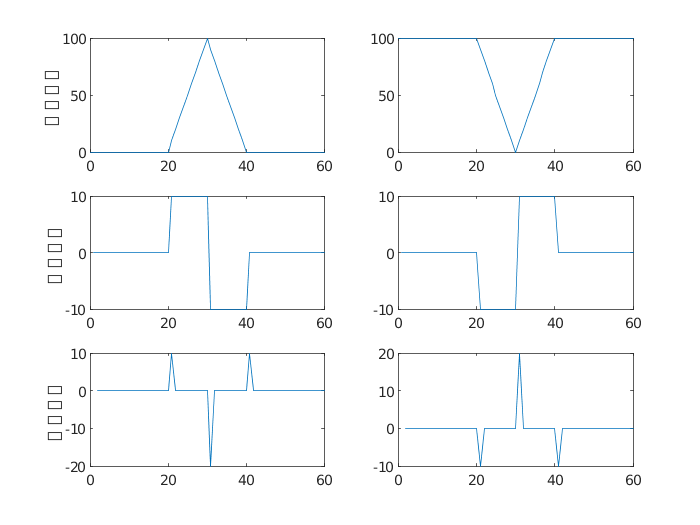
图6 渐变型细节
从图像的景物细节的灰度分布特性可知,有些灰度变化特性一阶微分的描述不是很明确,为此,采用二阶微分能够获得更丰富的景物细节。
2.Sobel边缘检测与锐化的实现
2.1.Sobel边缘检测算法理论
Robert算子只采用梯度微分锐化图像,会让噪声、条纹得到增强,而Sobel边缘检测算子则在一定程度上解决了这个问题,它是一种先求平均、再求微分、最后求梯度的算子,其算子形式如下所示。显然,Sobel算子只考虑了源像素点周围8个相邻像素点的水平和垂直方向的像素突变,而没有加入源像素点灰度值的计算。
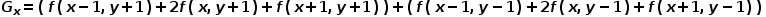
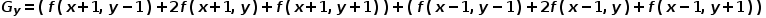
Sobel算子的水平和垂直模板如图12所示,分别对水平边缘和垂直边缘的影响最大。
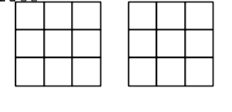
图12 Sobel算子模板
Sobel算子在一个方向求微分,而在另一个方向求平均,因而对噪声相对不敏感,具有抑制噪声的作用。由于像素平均相当于对图像进行低通滤波,所以Sobel算子对边缘的定位不如Robert算子。但与Robert算子相比,Sobel算子有一定的抗干扰性,图像效果比较干净。 利用算子模板可求得水平和垂直方向的梯度
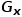 和
和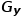 ,再通过梯度合成便可获得边缘检测结果
,再通过梯度合成便可获得边缘检测结果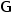 ,如下所示:
,如下所示:
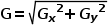
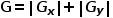
Sobel边缘检测的过程如图13所示,获得了比较粗的边界,但边缘定位精度不够高,,有时可能对非边缘像素的响应大于某些边缘处的响应或者响应差别不是很大,造成漏检或误检。当对精度要求不是很高时,是一种较为常用的边缘检测方法。将边缘检测结果与原图叠加便可以得到锐化后的图像,如图14所示。
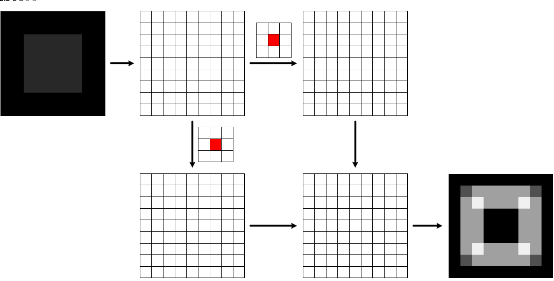
图13 Sobel边缘检测

图14 Sobel锐化
2.2.Sobel边缘检测Matlab实现
前面已经对Sobel边缘检测算法进行了介绍,现在基于Matlab软件对其进行仿真。创建函数Sobel_Edge_Detector用于实现Sobel算子对图像进行边缘检测,相关的matlab代码如下所示(详见Sobel_Edge_Detector.m)。
% 灰度图像Sobel边缘检测算法实现
% IMG为输入的灰度图像
% Q为输出的灰度图像
function Q = Sobel_Edge_Detector(IMG)
[h,w] = size(IMG); % 获取图像的高度h和宽度w
Q = zeros(h,w); % 初始化Q为全0的h*w大小的图像
% -------------------------------------------------------------------------
% Wx Wy Pixel
% [ -1 -2 -1 ] [ +1 0 -1] [ P1 P2 P3]
% [ 0 0 0 ] [ +2 0 -2] [ P4 P5 P6]
% [ +1 +2 +1 ] [ +1 0 -1] [ P7 P8 P9]
Wx = [-1,-2,-1;0,0,0;1,2,1]; % Weight x
Wy = [1,0,-1;2,0,-2;1,0,-1]; % Weight y
IMG = double(IMG);
for i = 1 : h
for j = 1 : w
if(i<2 || i>h-1 || j<2 || j>w-1)
Q(i,j) = 0; % 边缘像素不处理
else
% Gx = sum(Wx.*IMG(i-1:i+1,j-1:j+1),'all');
Gx = Wx(1,1)*IMG(i-1,j-1) + Wx(1,2)*IMG(i-1,j) + Wx(1,3)*IMG(i-1,j+1) +...
Wx(2,1)*IMG(i ,j-1) + Wx(2,2)*IMG(i ,j) + Wx(2,3)*IMG(i ,j+1) +...
Wx(3,1)*IMG(i+1,j-1) + Wx(3,2)*IMG(i+1,j) + Wx(3,3)*IMG(i+1,j+1);
% Gy = sum(Wy.*IMG(i-1:i+1,j-1:j+1),'all');
Gy = Wy(1,1)*IMG(i-1,j-1) + Wy(1,2)*IMG(i-1,j) + Wy(1,3)*IMG(i-1,j+1) +...
Wy(2,1)*IMG(i ,j-1) + Wy(2,2)*IMG(i ,j) + Wy(2,3)*IMG(i ,j+1) +...
Wy(3,1)*IMG(i+1,j-1) + Wy(3,2)*IMG(i+1,j) + Wy(3,3)*IMG(i+1,j+1);
% Q(i,j) = sqrt(Gx^2 + Gy^2);
Q(i,j) = abs(Gx) + abs(Gy);
end
end
end
Q=uint8(Q);
上述Matlab代码中需要注意以下几点:
(1)函数输入IMG是uint8数据类型的图像,而计算时存在负数和小数,需要用浮点数来表示,所以将IMG由uint8数据类型转为double数据类型;
(2)对图像边缘的像素不进行处理,直接输出0;
(3)将函数输出Q由double数据类型转为uint8数据类型。
接下来编写顶层M文件,相关的Maltab代码如下所示(详见Sobel_Sharpen_Test.m),Sobel锐化处理流程如图15所示。
clear all;
close all;
clc;
% -------------------------------------------------------------------------
% Read PC image to Matlab
IMG1 = imread('../../0_images/Lenna.jpg'); % 读取jpg图像
IMG1 = rgb2gray(IMG1);
subplot(131);imshow(IMG1);title('【1】原图');
% -------------------------------------------------------------------------
IMG2 = Sobel_Edge_Detector(IMG1);
subplot(132);imshow(IMG2);title('【2】Sobel边缘检测结果');
% -------------------------------------------------------------------------
IMG3 = IMG1 + IMG2;
subplot(133);imshow(IMG3);title('【3】Sobel锐化图像');
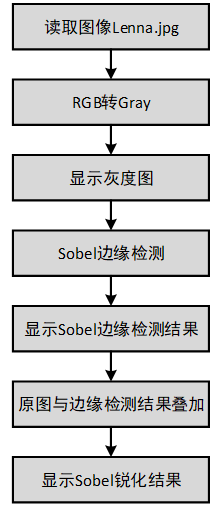
图15 Sobel锐化处理流程
执行顶层M文件可得到图16所示的结果,其中【2】是进行Sobel边缘检测得到的效果图,可以看出Sobel算子对边缘有较强的响应,与Robert算子相比,对边缘的响应更加强烈,得到的边缘更加宽;【3】是原图与边缘检测结果叠加后的效果图,相比原图,边缘和细节更加突出,但图像有些失真。

图16 Sobel边缘检测与锐化
审核编辑 :李倩
-
求教求教,红外图像锐化2012-04-01 1591
-
DSP c6722 图像锐化2016-05-12 3413
-
基于FPGA的图像拉普拉斯锐化处理2019-07-08 3109
-
8168采集图像直接播放锐化严重该怎么办?2019-08-26 1349
-
玩转Zynq连载45——[ex64] MT9V034摄像头的图像拉普拉斯锐化处理2019-12-26 3001
-
源码交流=图像处理 实现图像去噪、滤波、锐化、边缘检测2020-04-01 23981
-
锐化图像的MATLAB实现2020-05-06 24314
-
基于拉普拉斯算法的图像锐化算法实现2011-10-12 1448
-
JAVA教程之模糊与锐化2016-04-11 485
-
基于DSP_FPGA的红外图像锐化算法的实现2016-08-29 512
-
基于CORDIC的高速Sobel算法实现2018-10-05 4096
-
如何使用DSP和FPGA实现红外图像锐化算法的实现2021-01-25 1060
-
基于扩展相位拉伸变换的血管造影图像锐化2021-04-21 904
-
Sobel边缘检测与锐化的实现2022-03-21 3576
-
图像锐化的Sobel、Laplacian算子基础知识介绍2023-09-13 3069
全部0条评论

快来发表一下你的评论吧 !

