将格雷码转换为二进制编码器的方法

　　绝对编码器中的传感器输出格雷码序列，需要一些复杂的转换方法才能正确使用。本文展示了如何获取绝对编码器使用的格雷码并将其转换为二进制。

　　对于大多数使用电机和伺服机构的旋转运动，反馈至关重要。这种反馈通常采用编码器的形式。对于许多编码器，输出是“绝对的”，这意味着可以随时测量位置的精确度数，但它有一个缺点：它需要大量传感器。这些传感器经常输出格雷码序列，需要一些复杂的转换方法才能正确使用。

　　二进制如何导致编码器出现问题

　　电机和其他旋转运动设备最常见的反馈形式是编码器，它使用光（光学）传感器对着具有特定黑白图案的旋转盘来提供角位置数据。存在两种主要类型的编码器：增量式和绝对式。增量编码器对亮/暗标记转换进行计数，以跟踪在给定时间内经过了多少度的旋转。

　　另一种编码器是绝对型编码器，这种编码器经常使用，因为它可以测量与增量型相同的量，但它是由圆盘构成的，圆盘具有从中心辐射的复杂标记图案。根据位置的不同，图案是完全独特的。它们通常有 256 到 1024 个不同的独特图案，均匀分布在圆圈周围，分别表示 8 位或 10 位输出。

　　位数等于跟踪模式的传感器数量，而这个数量的传感器可能会为单个处理器创建一个耗时的读取任务。为了最大程度地减少读取错误，磁盘通常具有一种模式，该模式仅允许一个传感器读数在磁盘旋转时随时更改。

　　由于图案只有暗色或亮色，这为每个传感器提供了开/关或“二进制”输出。在典型的二进制模式中，位序列直接对应于一个等效的十进制数，该十进制数会在磁盘周围增加，从 0 到 256（或最多 1024）。标准二进制序列的唯一问题是多个位同时改变许多计数。每次发生这种情况时，都可能会遇到读取错误。

　　下表显示了这种情况发生的频率。

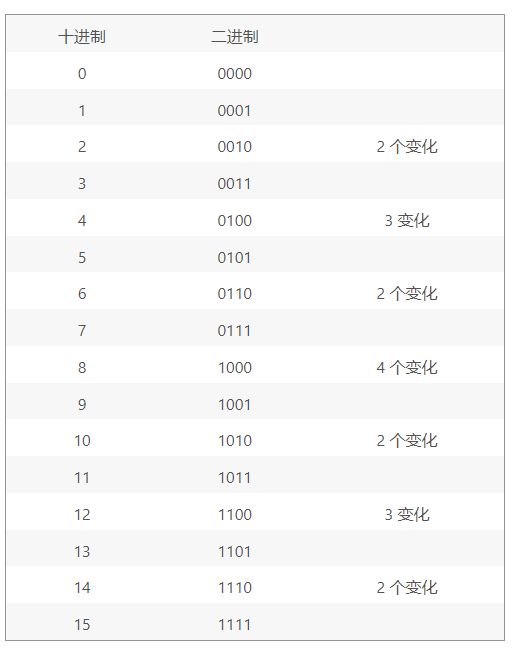
　　如图所示，这种可能的错误每隔一个计数就会发生一次，这是完全不可接受的。

　　为什么会出现这样的问题？

　　作为这个错误严重性的一个例子，想象一下从第九种模式到第十种模式的转变。四个传感器最初会读取 1001，然后在电机旋转时变为 1010。

　　控制器会以固定的快速间隔读取传感器，因此它可能会在模式仍为 9 时开始读取，因此前三个传感器可能会读取 1 0 和 0。然后，就在它读取最后一个传感器之前，模式步骤最多 10 并且最终传感器变为 0。

　　控制器会将整个序列串在一起为 1000。但看起来它只是倒退了，回到了 8！实际情况并非如此。

　　另一方面，如果只有一个位从一个计数转换到下一个计数，控制器将看到变化并识别运动，或者它不会看到变化并识别出还没有发生运动。格雷码是这种一次只更改一次的系统序列，但对于熟悉标准二进制的专业人士来说，这种模式似乎很陌生。

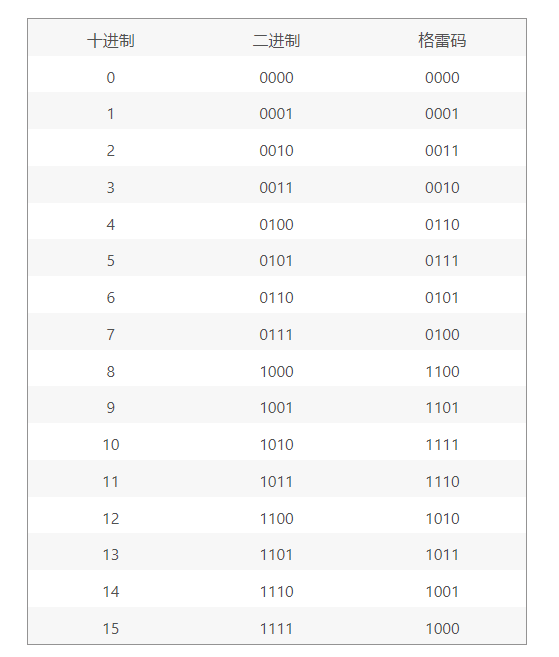
　　虽然它与标准二进制不匹配，但格雷码到二进制的计算可以非常简单地完成，这里有一些标准梯形逻辑和使用 C++ 的结构化文本中的示例。

　　梯形逻辑转换

　　要将格雷码位转换为正确的二进制位，每个格雷码传感器必须对应一个布尔值，或者直接来自传感器，或者作为整数的一部分。

　　此示例是用 Automation Direct 的梯形图编程软件编写的，并假设“Sensor_1”是最低有效位 （LSB），传感器沿着编码器磁盘的外边缘。共有八个传感器（8 位）增加到编码器的中心。

　　‘Binary_Number:1’ 是用于存储标准二进制等效值的整数的对应位。对于其他软件，例如 Rockwell 的 RSLogix，这个整数位可能看起来像 Binary_Number.0，其中 Binary_Number 是一个 INT 类型标记，从位 0 开始。

　　第 1 行 - 为了正确转换，最高有效位 （MSB） 即 Sensor_8 保持不变。

　　第 2 行 - 对于下一个有效位，在 Sensor_8 和 Sensor_7 之间使用“异或”的逻辑比较。如果 Sensor_7 和 _8 相同，则返回 0，如果 Sensor_7 和 _8 不同，则返回 1。

　　第 3 到 8 行 - 对于每个剩余位，我们继续在前一个位和下一个 Sensor 值之间使用“异或”。

　　如果编码器是 10 位的，则有 10 行，前两行将使用 Sensor_10 和 _9 并下降，直到最后使用最后一个传感器。

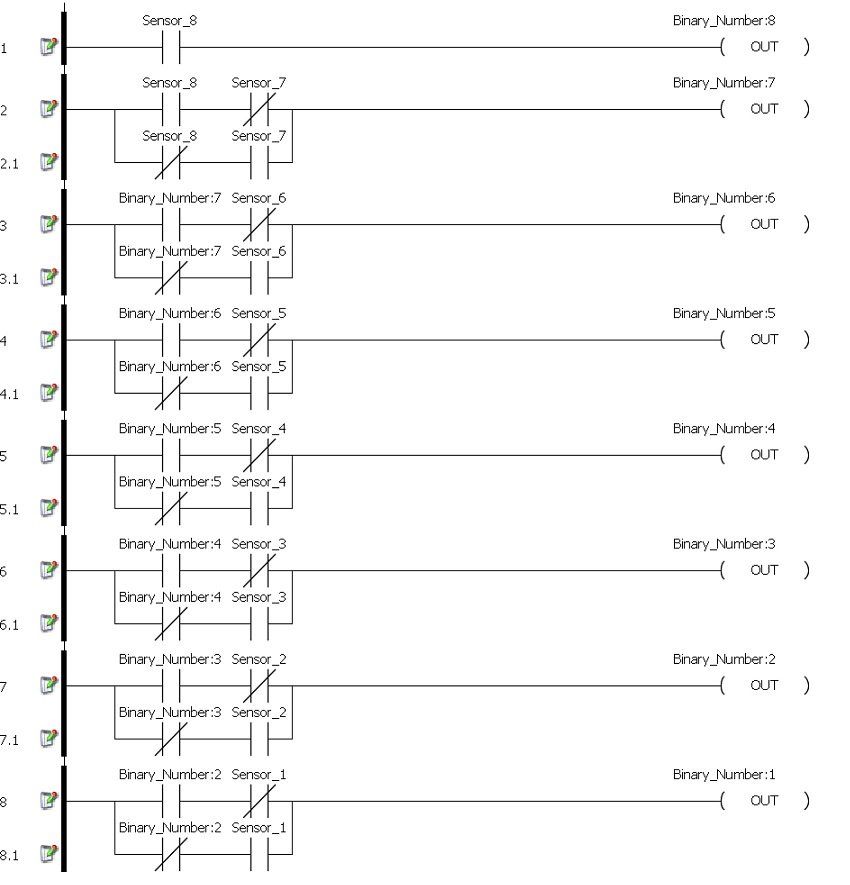
　　图 1. Automation Direct 梯形图编程软件中使用的梯形逻辑示例。

　　所有前面的逻辑线都可以包装到单个自定义指令块或子程序中以简化过程。

　　结构化文本转换

　　这个例子只是部分的，因为有各种各样的语言、语法和应用程序。核心目标仍然是将来自八个传感器的传感器读数转换为等效的二进制数。

　　对于基于 C 的语言，产生单个位的异或 （XOR） 是 ！=。MSB 与传感器值相同，第二位是两个传感器的 XOR，其余每个位是前一位和下一个传感器的 XOR。

　　无效转换（）{

　　Binary_Number_8 = Sensor_8；

　　Binary_Number_7 = Sensor_8 ！= Sensor_7；

　　Binary_Number_6 = Binary_Number_7 ！= Sensor_6;

　　Binary_Number_5 = Binary_Number_6 ！= Sensor_5;

　　Binary_Number_4 = Binary_Number_5 ！= Sensor_4;

　　Binary_Number_3 = Binary_Number_4 ！= Sensor_3;

　　Binary_Number_2 = Binary_Number_3 ！= Sensor_2;

　　Binary_Number_1 = Binary_Number_2 ！= Sensor_1;

　　}

　　剩下的步骤是将 Binary_Number 位转换为适合应用程序的整数。请注意，不同的语言可能遵循不同的程序。此示例仅用于概述该过程的外观。