

一文解析通信系统的高效正交变量优化算法
描述
本文讨论了一种算法,用于在具有正交输入向量的二维空间中找到最佳调整点。该算法根据测量数据点求解相交圆的方程。
几个关键的系统性能指标由对应于幅度和相位的正交输入参数确定;两个例子是正交调制器载波馈通和边带抑制。这些参数通过优化调制器正交基带输入之间的直流偏移平衡和幅度和相位平衡得到改善。
因为在给定二维空间的情况下找到这些参数的最优调整并不是一件容易的事,所以在本文中,我将讨论一种 Python 算法,用于在具有正交输入向量的二维空间中找到最优调整点。该算法根据测量数据点求解相交圆的方程,并在少至四次迭代中找到最佳点。为了举例说明该技术,我使用了德州仪器 (TI) AFE7070集成数模转换器 (DAC) 以及正交调制器载波馈通参数。
优化杂散发射
通信系统努力将杂散发射降至最低。其中一些杂散发射源于正交输入信号失配。例如,直流偏移失配和幅度/相位失衡将分别影响模拟正交调制器中的载波馈通和边带抑制参数。将输入变量调整到最佳设定点可以最大限度地减少杂散输出。
图 1 将测量参数表示为从优化点 [x0,y0] 到二维平面上实际点的矢量幅度 (r)。参数值以单位圆[0,1]为界。0 表示完全消除或无信号,1 表示无消除或完全信号。在分贝尺度中,该函数受 [-inf,0] 的约束。半径为 r 的圆代表所有可能达到相同大小的 x,y 点。
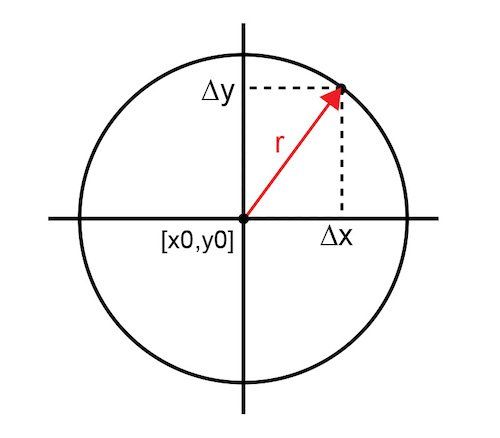
图 1. 从优化点到实际点的向量
等式 1 以最简单的形式表示该函数:
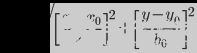
常数 [a0,b0] 表示系统相关的归一化因子,以保持最大结果小于 1。从技术上讲,等式 1 描述了一个椭圆,因为每个自变量的比例因子不需要相同。为简单起见,a0 等于 b0,因此曲线是真正的圆。
目标是尽快找到使测量参数 (r) 最小化的最佳点 [x0,y0]。通过统计变化的输入参数有效地找到该点具有挑战性。传统的狩猎和啄食方法使用连续试验来缩小到最佳点。尽管这会产生所需的解决方案,但当收敛时间很关键时需要进行太多迭代,因此需要一种新方法。
相交的圆
理想情况下,使用相交圆的精确三个测量迭代确定最佳点。在任意输入点 [x1,y1] 处的第一个测量结果定义了由半径为 r1 的圆 A 表示的最优点的无限可能性。添加第二个数据点会产生另一个由圆圈 B 表示的无限数据集;然而,两个圆的交点将解缩小到两点。第三个数据点和相应的圆 C 提供了第三条曲线,其中只有一个相互交叉点。该交点是最佳点。图 2 显示了最终确定最佳点的相交圆的进程。
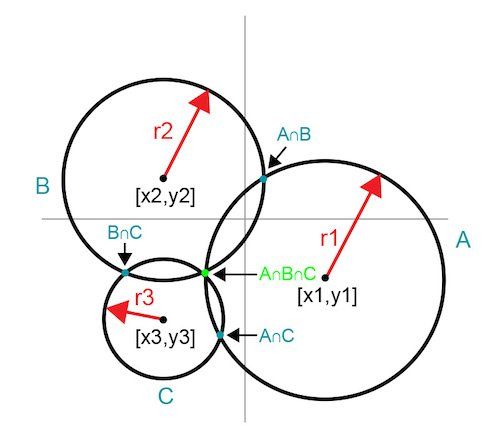
图 2. 相交的圆揭示了一个共同的交点
这种技术在恰好三个迭代中揭示了最佳点。第四次迭代测量最佳点以确认和记录结果。
图 3 说明了一种通过使用 xy 平面中经验已知的边界信息来消除一次迭代的技术。在其中一个边界点处选择初始点,使第一条曲线 (A) 为 90 度圆弧。通过沿 x 或 y 方向移动选择第一个弧上的第二个点。
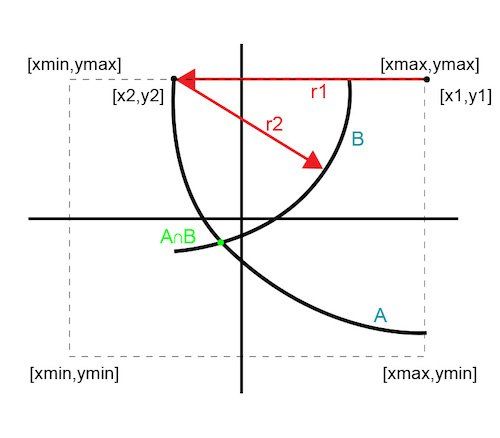
图 3. 两次迭代解决方案
由于第二个点仍然在边界边上,所以它的曲线是一个低于 180 度的弧。这两条曲线的交点提供了一个最佳点。这种方法仅在两次迭代中就揭示了最佳点,并通过三次来确认。
逐次圆逼近
最优解取决于数学方程的准确性。在实际测量情况下,一些假设或错误会影响结果。测量的信号非常小;噪声和测量容差会引入误差。使用完美的圆而不是椭圆会引入一些不确定性。求解多个方程所需的比例因子假设也引入了不确定性。这些错误和假设转化为曲线的模糊性。
图 4 说明了模糊曲线如何不能保证精确的交点;相反,它们定义了一个收敛区域。
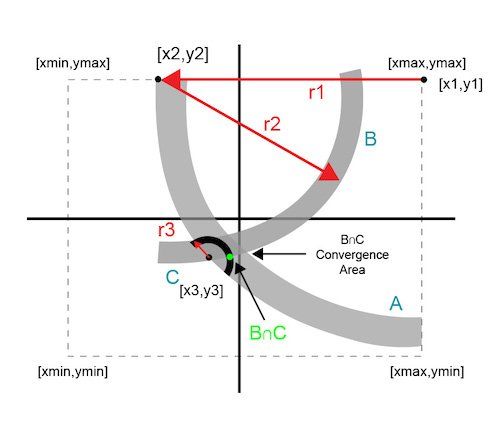
图 4. 连续圆相交近似
每个附加数据点都使用上一次迭代的数据。连续的圆圈会聚到系统最小阈值内的解决方案区域。
测量示例
该示例使用 AFE7070 DAC 并针对载波馈通参数进行优化。AFE7070 是一个方便的平台,因为集成了 DAC 和调制器。调制器正交输入上的 DC 失调不平衡决定了载波馈通性能。AFE7070 具有内部数字调谐功能,可精确控制 DC 偏移平衡。不需要太多;分辨率为微伏级。
该示例的 x,y 参数是整数数字阶跃值,用于控制正交输入上的 DC 电平。设备的先前统计采样提供了输入变量的 x、y 范围以及计算中使用的步骤表。步进表提供了以分贝毫瓦为单位的测量载波馈通到 delta-x(或 delta-y)因子的“转换”。
高(或换句话说,差)测量值意味着设置偏离并且需要更大的增量才能达到最佳点。相反,低值意味着设定点接近并且需要进行小的修正。这一点“功课”对于确保初始猜测点不会太远,并将迭代时间减少到最低限度是必要的。
图 5 显示了 Python 算法,它在四次或更少的迭代中找到最佳输入变量。

图 5. Python 优化算法
函数“Get_r”和“GetCFi”是特定于设备的测量。为简洁起见,我省略了代码,因为它对于演示优化算法无关紧要。在您的应用程序中,这些功能与系统中设备参数的编程和测量有关。
结论
对于 AFE7070 DAC,在大多数情况下,该算法可在 3 次迭代内优化载波馈通,并在不到 1.7 秒内优化,主要由频谱分析仪建立和扫描时间进行选通。之前的步骤方法需要近 20 次迭代和 20 多秒才能完成。与传统方法相比,该算法的速度提高了 10 倍以上。依赖于增益和相位的正交输入变量的其他通信系统参数也可以使用该算法来有效地找到最优解。
-
一种适用于无线通信系统的半盲ICA算法2010-04-23 1493
-
seo优化的百度算法笔记2019-05-27 1992
-
一文解析Vue代码层面的优化2020-10-27 2119
-
多目标优化算法有哪些2021-07-12 1489
-
用于全局优化的混合正交遗传算法2009-03-25 443
-
正交遗传算法在网络优化设计中的应用2009-08-19 561
-
网络监管系统爬网算法优化2009-09-17 376
-
参数优化模型的正交逼近算法2010-02-10 818
-
高阶FIR正交镜像滤波器的设计2011-08-29 813
-
基于机器学习算法的SVM优化2017-10-18 4532
-
基于离散化正交匹配追踪的中继混合预编码算法2021-03-31 900
-
剖析正交匹配追踪算法的优化设计与FPGA实现2021-04-08 3106
-
基于LSPIA的NURBS曲线拟合优化算法2021-04-27 1368
-
300M钢正交切削加工变量相关实验测试2021-04-30 879
-
一文解析域控制的概念和变量2022-09-14 752
全部0条评论

快来发表一下你的评论吧 !

