如何使用TensorFlow构建和训练变分自动编码器

　　多年来，我们已经看到许多领域和行业利用人工智能 （AI） 的力量来推动研究的边界。数据压缩和重建也不例外，人工智能的应用可以用来构建更强大的系统。

　　在本文中，我们将研究一个非常流行的 AI 用例，用于压缩数据并使用自动编码器重建压缩数据。

　　自动编码器应用

　　自动编码器在机器学习领域引起了许多人的关注，这一事实通过自动编码器的改进和几种变体的发明变得显而易见。他们在神经机器翻译、药物发现、图像去噪等几个领域取得了一些有希望的（如果不是最先进的）结果。

　　自动编码器的组成部分

　　与大多数神经网络一样，自编码器通过反向传播梯度来优化一组权重——但自编码器架构与大多数神经网络架构之间最显着的区别是瓶颈。这个瓶颈是将我们的数据压缩成较低维度的表示的一种手段。自编码器的另外两个重要部分是编码器和解码器。

　　将这三个组件融合在一起形成了一个“香草”自动编码器，尽管更复杂的自动编码器可能有一些额外的组件。

　　让我们分别看一下这些组件。

　　编码器

　　这是数据压缩和重建的第一阶段，它实际上负责数据压缩阶段。编码器是一个前馈神经网络，它接收数据特征（例如图像压缩中的像素）并输出一个大小小于数据特征大小的潜在向量。

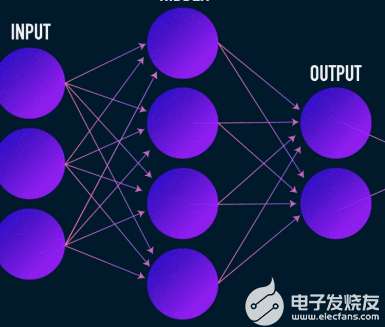
　　为了使数据的重建具有鲁棒性，编码器在训练期间优化其权重，以将输入数据表示的最重要特征压缩到小型潜在向量中。这确保了解码器有足够的关于输入数据的信息来以最小的损失重建数据。

　　潜在向量（瓶颈）

　　自编码器的瓶颈或潜在向量分量是最关键的部分——当我们需要选择它的大小时，它变得更加关键。

　　编码器的输出为我们提供了潜在向量，并且应该包含我们输入数据的最重要的特征表示。它还用作解码器部分的输入，并将有用的表示传播到解码器进行重建。

　　为潜在向量选择更小的尺寸意味着我们可以用更少的输入数据信息来表示输入数据特征。选择更大的潜在向量大小会淡化使用自动编码器进行压缩的整个想法，并且还会增加计算成本。

　　解码器

　　这个阶段结束了我们的数据压缩和重建过程。就像编码器一样，这个组件也是一个前馈神经网络，但它在结构上看起来与编码器有点不同。这种差异来自这样一个事实，即解码器将一个比解码器输出更小的潜在向量作为输入。

　　解码器的功能是从与输入非常接近的潜在向量生成输出。

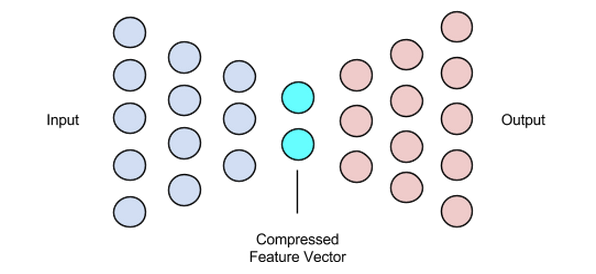
　　训练自动编码器

　　通常，在训练自动编码器时，我们将这些组件一起构建，而不是独立构建。我们使用梯度下降或 ADAM 优化器等优化算法对它们进行端到端训练。

　　损失函数

　　值得讨论的自动编码器训练过程的一部分是损失函数。数据重建是一项生成任务，与其他机器学习任务不同，我们的目标是最大化预测正确类别的概率，我们驱动我们的网络产生接近输入的输出。

　　我们可以通过几个损失函数来实现这个目标，例如 l1、l2、均方误差等。这些损失函数的共同点是它们测量输入和输出之间的差异（即多远或相同），使它们中的任何一个成为合适的选择。

　　自动编码器网络

　　一直以来，我们一直在使用多层感知器来设计我们的编码器和解码器——但事实证明，我们可以使用更专业的框架，例如卷积神经网络 （CNN） 来捕获更多关于输入数据的空间信息图像数据压缩的情况。

　　令人惊讶的是，研究表明，用作文本数据自动编码器的循环网络工作得非常好，但我们不打算在本文的范围内进行讨论。多层感知器中使用的编码器-潜在向量-解码器的概念仍然适用于卷积自动编码器。唯一的区别是我们设计了带有卷积层的解码器和编码器。

　　所有这些自动编码器网络都可以很好地完成压缩任务，但存在一个问题。

　　我们讨论过的网络创造力为零。我所说的零创造力的意思是他们只能产生他们已经看到或接受过培训的输出。

　　我们可以通过稍微调整我们的架构设计来激发一定程度的创造力。结果被称为变分自动编码器。

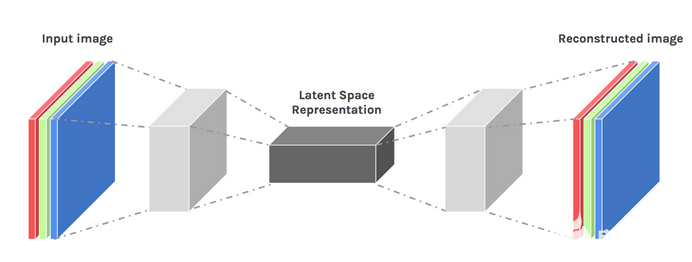
　　变分自编码器

　　变分自动编码器引入了两个主要的设计变化：

　　我们没有将输入转换为潜在编码，而是输出两个参数向量：均值和方差。

　　一个称为 KL 散度损失的附加损失项被添加到初始损失函数中。

　　变分自动编码器背后的想法是，我们希望我们的解码器使用从由编码器生成的均值向量和方差向量参数化的分布中采样的潜在向量来重建我们的数据。

　　从分布中采样特征给解码器一个受控的空间来生成。在训练变分自动编码器后，每当我们对输入数据执行前向传递时，编码器都会生成一个均值和方差向量，负责确定从哪个分布中对潜在向量进行采样。

　　平均向量决定了输入数据的编码应该集中在哪里，方差决定了我们想要从中选择编码以生成真实输出的径向空间或圆。这意味着，对于相同输入数据的每次前向传递，我们的变分自动编码器可以生成以均值向量为中心和方差空间内的不同输出变体。

　　相比之下，在查看标准自动编码器时，当我们尝试生成网络尚未训练的输出时，由于编码器产生的潜在向量空间的不连续性，它会生成不切实际的输出。

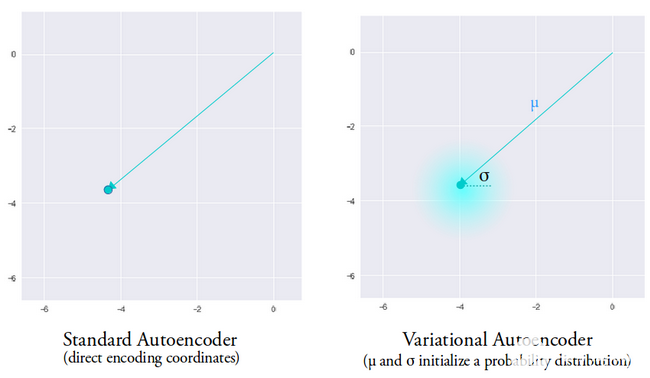
　　现在我们对变分自动编码器有了一个直观的了解，让我们看看如何在 TensorFlow 中构建一个。

　　用于变分自动编码器的 TensorFlow 代码

　　我们将从准备好数据集开始我们的示例。为简单起见，我们将使用 MNIST 数据集。

　　（train_images， _）， （test_images， _） = tf.keras.datasets.mnist.load_data（）

　　train_images = train_images.reshape（train_images.shape［0］， 28， 28， 1）.astype（‘float32’）

　　test_images = test_images.reshape（test_images.shape［0］， 28， 28， 1）.astype（‘float32’）

　　# Normalizing the images to the range of ［0.， 1.］

　　train_images /= 255.

　　test_images /= 255.

　　# Binarization

　　train_images［train_images 》= .5］ = 1.

　　train_images［train_images 《 .5］ = 0.

　　test_images［test_images 》= .5］ = 1.

　　test_images［test_images 《 .5］ = 0.

　　TRAIN_BUF = 60000

　　BATCH_SIZE = 100

　　TEST_BUF = 10000

　　train_dataset = tf.data.Dataset.from_tensor_slices（train_images）.shuffle（TRAIN_BUF）.batch（BATCH_SIZE）

　　test_dataset = tf.data.Dataset.from_tensor_slices（test_images）.shuffle（TEST_BUF）.batch（BATCH_SIZE）

　　Obtain dataset and prepare it for the task.

　　class CVAE（tf.keras.Model）：

　　def __init__（self， latent_dim）：

　　super（CVAE， self）.__init__（）

　　self.latent_dim = latent_dim

　　self.inference_net = tf.keras.Sequential（

　　［

　　tf.keras.layers.InputLayer（input_shape=（28， 28， 1）），

　　tf.keras.layers.Conv2D（

　　filters=32， kernel_size=3， strides=（2， 2）， activation=‘relu’），

　　tf.keras.layers.Conv2D（

　　filters=64， kernel_size=3， strides=（2， 2）， activation=‘relu’），

　　tf.keras.layers.Flatten（），

　　# No activation

　　tf.keras.layers.Dense（latent_dim + latent_dim），

　　］

　　）

　　self.generative_net = tf.keras.Sequential（

　　［

　　tf.keras.layers.InputLayer（input_shape=（latent_dim，）），

　　tf.keras.layers.Dense（units=7*7*32， activation=tf.nn.relu），

　　tf.keras.layers.Reshape（target_shape=（7， 7， 32）），

　　tf.keras.layers.Conv2DTranspose（

　　filters=64，

　　kernel_size=3，

　　strides=（2， 2），

　　padding=“SAME”，

　　activation=‘relu’），

　　tf.keras.layers.Conv2DTranspose（

　　filters=32，

　　kernel_size=3，

　　strides=（2， 2），

　　padding=“SAME”，

　　activation=‘relu’），

　　# No activation

　　tf.keras.layers.Conv2DTranspose（

　　filters=1， kernel_size=3， strides=（1， 1）， padding=“SAME”），

　　］

　　）

　　@tf.function

　　def sample（self， eps=None）：

　　if eps is None：

　　eps = tf.random.normal（shape=（100， self.latent_dim））

　　return self.decode（eps， apply_sigmoid=True）

　　def encode（self， x）：

　　mean， logvar = tf.split（self.inference_net（x）， num_or_size_splits=2， axis=1）

　　return mean， logvar

　　def reparameterize（self， mean， logvar）：

　　eps = tf.random.normal（shape=mean.shape）

　　return eps * tf.exp（logvar * .5） + mean

　　def decode（self， z， apply_sigmoid=False）：

　　logits = self.generative_net（z）

　　if apply_sigmoid：

　　probs = tf.sigmoid（logits）

　　return probs

　　return logits

　　这两个代码片段准备了我们的数据集并构建了我们的变分自动编码器模型。在模型代码片段中，有几个辅助函数来执行编码、采样和解码。

　　计算梯度的重新参数化

　　有一个我们尚未讨论的重新参数化函数，但它解决了我们的变分自动编码器网络中的一个非常关键的问题。回想一下，在解码阶段，我们从由编码器生成的均值和方差向量控制的分布中对潜在向量编码进行采样。这在通过我们的网络前向传播数据时不会产生问题，但在从解码器到编码器的反向传播梯度时会导致一个大问题，因为采样操作是不可微的。

　　简单来说，我们无法从采样操作中计算梯度。

　　这个问题的一个很好的解决方法是应用重新参数化技巧。其工作原理是首先生成均值为 0 和方差为 1 的标准高斯分布，然后使用编码器生成的均值和方差对该分布执行可微加法和乘法运算。

　　请注意，我们在代码中将方差转换为对数空间。这是为了确保数值稳定性。引入了额外的损失项Kullback-Leibler 散度损失，以确保我们生成的分布尽可能接近均值为 0 方差为 1 的标准高斯分布。

　　将分布的均值驱动为零可确保我们生成的分布彼此非常接近，以防止分布之间的不连续性。接近 1 的方差意味着我们有一个更适中的（即，不是很大也不是很小）的空间来生成编码。

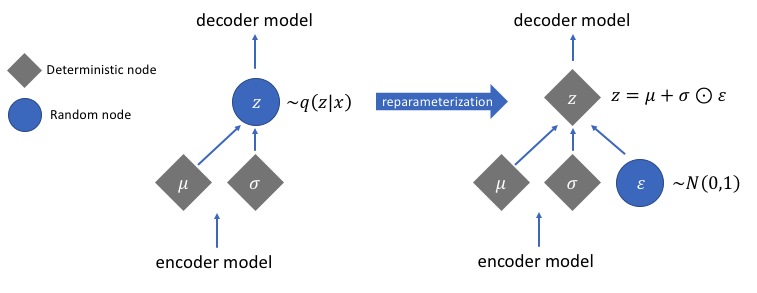
　　执行重新参数化技巧后，通过将方差向量与标准高斯分布相乘并将结果与​​均值向量相加得到的分布与均值和方差向量立即控制的分布非常相似。

　　构建变分自编码器的简单步骤

　　让我们通过总结构建变分自动编码器的步骤来结束本教程：

　　构建编码器和解码器网络。

　　在编码器和解码器之间应用重新参数化技巧以允许反向传播。

　　端到端训练两个网络。