如何补偿运算放大器的输入电容

了解输入端寄生电容的影响以及如何在模拟电路设计中对其进行补偿。

大多数内部补偿运算放大器旨在以任何与频率无关的闭环增益（包括单位增益）稳定运行。

在实践中，电容的存在，无论是有意的还是寄生的，都会使电路不稳定，并且可能需要用户采取额外的补偿措施来恢复可接受的相位裕度。

输出端有意电容的示例见于采样保持电路、峰值检测器和具有输出电容旁路的电压参考升压器。

本文将讨论输入端，尤其是反相输入端的寄生（或杂散）电容的影响。 

输入电容的类型

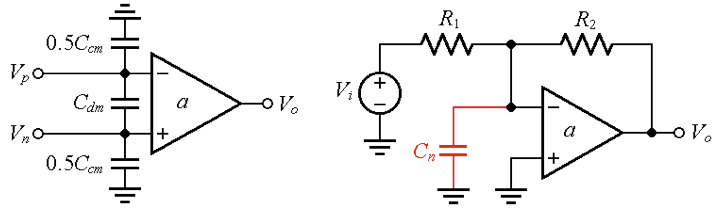
所有运算放大器都具有差模输入电容C dm和共模（输入连接在一起）输入电容C cm。这些是输入级晶体管以及输入保护二极管（如果存在）所表现出的电容。（即使C dm和C cm位于运算放大器内部，我们也将它们显示在外部以便更好地可视化。）

在物理电路中，额外的电容会在外部发挥作用，例如电阻器、它们的引线和印刷电路迹线的杂散电容。

在图 1b的放大器示例中，与反相输入相关的所有寄生参数都集中到一个等效电容Cn中。 

(一) (二)

图 1. (a) 运算放大器的杂散输入电容。(b) 将与反相输入相关的所有寄生参数集中为单个电容Cn。

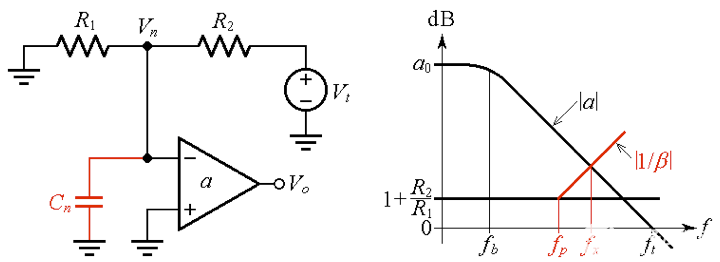
让我们通过闭合率 (ROC)来研究C n对电路稳定性的影响。为此，我们将输入源设置为零，按照图 2a（下图）断开环路，施加测试电压Vt，并计算反馈因子ß ( jf )为

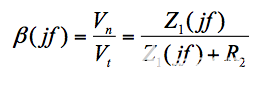
等式 1

(一) (二)

图 2。(a) 找到反馈因子 ß(jf)。(b) 接近 40 dB/dec 的闭合率 (ROC)。

在哪里

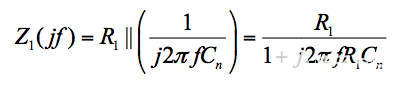
等式 2

代入等式（1），我们得到，经过一些代数操作，

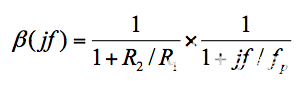
等式 3

在哪里

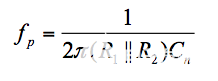
等式 4

如果我们关注等式 (4) 的物理意义，我们会看到C n和电阻R 1 || 由周围电路提供给它的R 2在反馈回路内建立一个极点频率。因此，在环路中传播的信号将不得不与两个极点竞争，一个由运算放大器引起，另一个由 Cn 引起，存在相移接近 180° 的风险，从而危及电路稳定性。

我们可以在图 2b中更好地可视化这一点，它显示了开环增益 |a| 的图。和反馈因子的倒数 |1/ ß ( jf )|，其中

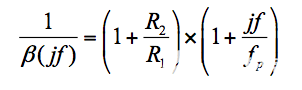
等式 5

ß ( jf )的极点频率 f p是1/ ß ( jf )的零频率，表明 |1/ ß ( jf )| 曲线在f p处开始上升。如果f p与交叉频率f x相比足够低，则闭合率将接近 40 dB/dec，表明相位裕度接近零。

如何减轻单个等效电容引起的相位滞后

对抗由C n引起的相位滞后的常用方法是通过跨R 2的反馈电容C f引入相位超前，如图 3 所示。

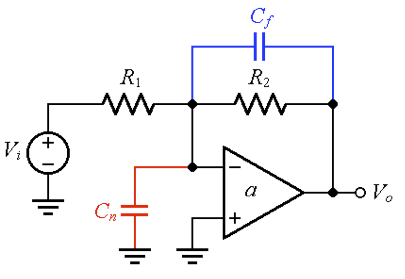
图 3。利用 C f引入的相位超前来对抗由 C n引起的相位滞后。

如果我们将R 2替换为Z 2 ( jf ) = R 2 ||( 1/j2πƒC f ) ，等式 (1) 仍然成立。这给出了，经过一些代数操作，

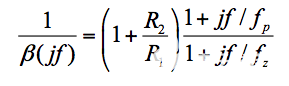
等式 6

在哪里

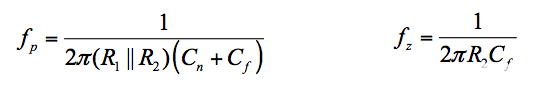
等式 7

这里需要注意的重要一点是，反馈电容的存在为ß ( jf ) 创建了一个零频率 fz，同时也稍微降低了现有的极点频率 fp（回想一下，ß 的极点/零点变成了1/ ß )。

如何选择反馈电容

选择C f 有两种常用方法：

fz = fp  _  _

fz =  fx _

fz = fp  _  _

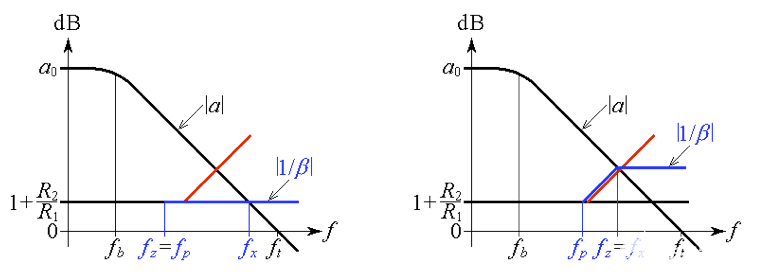
施加f z = f p 以使零抵消等式 (6) 中的极点，从而得到 1/ ß = 1 + R 2  / R 1，如图 4a所示。

(一) (二)

图 4.对于相位裕度 ɸ m ≈ 90°，施加 (a) f z = f p ，或 (b) f z = f x对于 ɸ m ≈ 45°。

使等式(7) 的f z和f p相等，经过简化后，

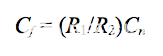
公式 8

C f的这种选择导致大约 90° 的相位裕度。为了找到交叉频率fx ，我们利用 | 上的增益带宽乘积的恒定性。一个| 要写的曲线 (1 + R 2  / R 1 ) × f x = f t，所以

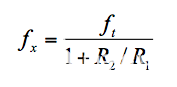
等式 9

请注意，闭环增益有两个极点频率f z和f x，其 –3-dB 频率接近f z。

fz =  fx _

施加f z = f x，如图 4b所示，相位裕度约为 45°。闭环增益现在将具有更高的–3-dB 频率，但代价是一些峰值和振铃。

要找到所需的C f，我们必须首先找到f x。考虑到 1/ ß的高频渐近线是 1 + C n  / C f，我们再次利用 | 上增益带宽乘积的恒定性。一个| 要写的曲线 (1 + C n  / C f ) × f x = f t，所以f x = f t  /(1 + C n  / C f )。

强加f z = f x意味着强加 1/( 2πR 2 C f ) = f t  /(1 + C n  / C f )。预期C n  / C f >> 1，我们近似 1/( 2πR 2 C f ) ≈ f t  /( C n  / C f ) = f t C f  / C n，我们求解C f得到

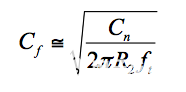
等式 10

请注意，闭环增益现在在f x处有两个重合的极点频率。

通过 PSpice 进行验证

我们希望通过图 5 的电路来验证上述考虑，该电路使用f t = 10 MHz 的恒定增益带宽运算放大器。

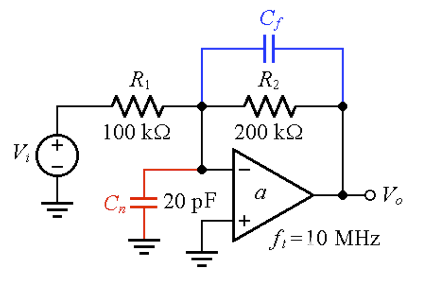
图 5。增益为 –2 V/V 的反相放大器示例。

现在让我们看一下图 6：

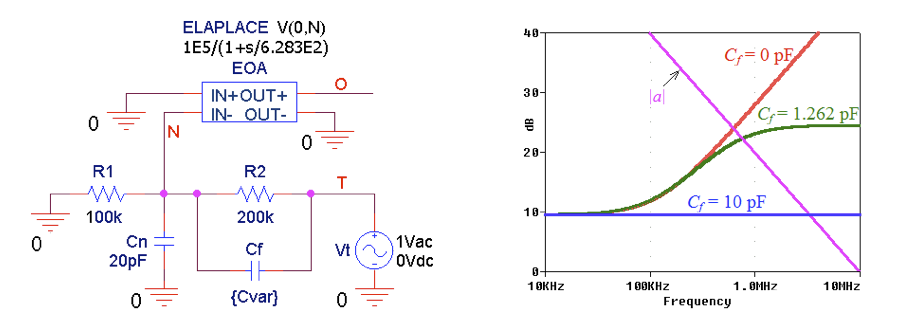
图 6.绘制 |a| 的 PSpice 电路 和 |1/ß|。(b) |1/ß| 不同 C f值的曲线。

参考图 6，我们做了以下考虑：

在没有补偿 ( C f = 0) 的情况下，交越频率测量为f x ≈ 625 kHz，相位角测量为 ph[ a ( jf x )] ≈ –90° 和 ph[1/ ß ( jf x ) ] ≈ 79.2°，所以

ɸ m = 180° + ph[ a ( jf x )] – ph[1/ ß ( jf x )] ≈ 180 – 90 –79.2 = 10.8°

等式 11

表示电路处于振荡边缘。

对于ɸ m ≈ 90° 的相位裕度，我们使用等式 (8) 得到C f = 10 pF。根据等式 (9)，我们得到f x ≈ 3.33 MHz。如图 6b所示，我们现在有 

ɸ m ≈ 90°。

对于ɸ m ≈ 45°，我们使用等式 (10) 得到C f = 1.262 pF。使用 PSpice 的光标，我们现在测量f x = 762.1 kHz 和ɸ m = 58.8°。这比预期的 45° 要好。要了解原因，使用公式 (7) 计算f p = 112.28 kHz 和f z = 630.57 kHz，然后使用公式 (6) 计算 

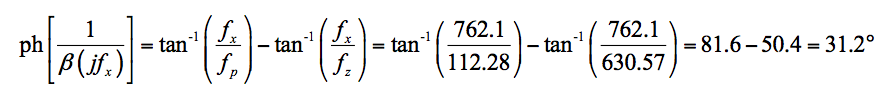
然后，按式（11）的方式进行，求ɸ m = 180°– 90 –31.2 = 58.8°。

闭环交流响应

图 7 所示为所考虑的三种情况的闭环交流响应。

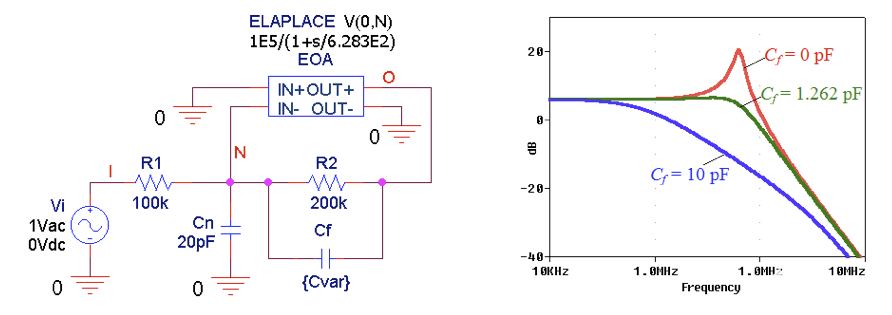
图 7.使用 PSpice 绘制不同 C f值的闭环交流响应。

正如预期的那样，未补偿的响应表现出相当多的峰值。对于C f = 1.262 pF，峰值几乎不明显，在这种情况下，响应在大约 762 kHz 处表现出一对重合的极点频率。C f = 10 pF的响应是最迟缓的，这是我们为大相位裕度付出的代价。

如前所述，该响应包含两个极点频率，即f z和f x。

图 8 中显示的是阶跃响应，在讨论了交流响应之后，它应该是不言自明的。

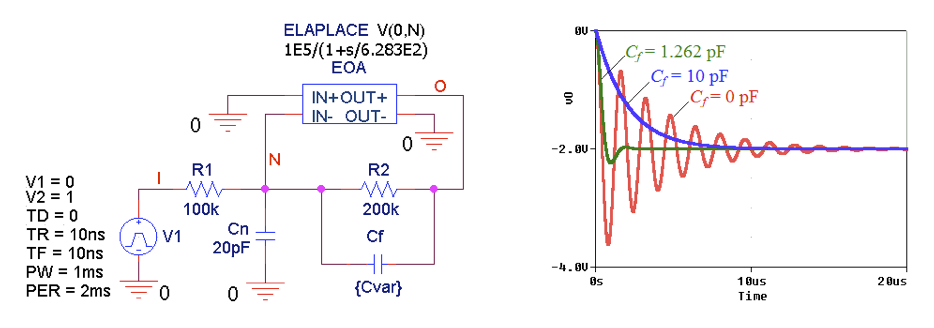
图 8.使用 PSpice 绘制不同 Cf 值的闭环阶跃响应。

杂散电容总是坏事吗？

值得指出的是，杂散电容虽然通常是不可取的，但并不一定总是一个诅咒。

假设所考虑的电路是在R 1 = 1.0 kΩ 和R 2 = 2.0 kΩ 的情况下实现的，也就是说，数值按比例缩小了20 倍，同时仍确保相同的 –2 V/V 闭环增益。然后，根据等式 (4)，f p将按比例放大20 倍，达到远远超过f x的值，因此无需进行补偿。

当然，这种优势的代价是通过降低电阻来增加功耗。作为一项练习，您可以了解在没有补偿的情况下实现 60° 的相位裕度需要多低的电阻缩放比例。