

如何计算Texture Functions的纹理函数返回值
描述
本附录给出了用于计算 Texture Functions 的纹理函数返回值的公式,具体取决于纹理引用的各种属性(请参阅纹理和表面内存)。
绑定到纹理引用的纹理表示为一个数组 T
一维纹理的 N 个texels,
二维纹理的 N x M texels,
三维纹理的 N x M x L texels。
它是使用非归一化纹理坐标 x、y 和 z 或归一化纹理坐标 x/N、y/M 和 z/L 获取的,如纹理内存中所述。 在本附录中,假定坐标在有效范围内。 纹理内存解释了如何根据寻址模式将超出范围的坐标重新映射到有效范围。
J.1. Nearest-Point Sampling
在这种过滤模式下,纹理获取返回的值是
tex(x)=T[i] 对于一维纹理,
tex(x,y)=T[i,j] 对于二维纹理,
tex(x,y,z)=T[i,j,k] 对于三维纹理,
其中 i=floor(x),j=floor(y),k=floor(z)。
下图 说明了 N=4 的一维纹理的最近点采样。
对于整数纹理,纹理获取返回的值可以选择重新映射到 [0.0, 1.0](请参阅纹理内存)。

J.2. Linear Filtering
在这种仅适用于浮点纹理的过滤模式下,纹理获取返回的值是
tex(x)=(1−α)T[i]+αT[i+1] for a one-dimensional texture,
tex(x,y)=(1−α)(1−β)T[i,j]+α(1−β)T[i+1,j]+(1−α)βT[i,j+1]+αβT[i+1,j+1] for a two-dimensional texture,
tex(x,y,z) =(1−α)(1−β)(1−γ)T[i,j,k]+α(1−β)(1−γ)T[i+1,j,k]+(1−α)β(1−γ)T[i,j+1,k]+αβ(1−γ)T[i+1,j+1,k]+(1−α)(1−β)γT[i,j,k+1]+α(1−β)γT[i+1,j,k+1]+(1−α)βγT[i,j+1,k+1]+αβγT[i+1,j+1,k+1]for a three-dimensional texture,
其中:
i=floor(xB), α=frac(xB), xB=x-0.5,
j=floor(yB), β=frac(yB), yB=y-0.5,
k=floor(zB), γ=frac(zB), zB= z-0.5,
α、β 和 γ 以 9 位定点格式存储,带有 8 位小数值(因此精确表示 1.0)。
下图 说明了 N=4 的一维纹理的线性过滤。
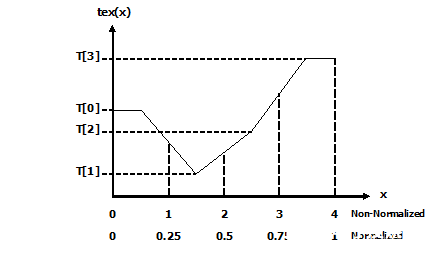
J.3. Table Lookup
x 跨越区间 [0,R] 的查表 TL(x) 可以实现为 TL(x)=tex((N-1)/R)x+0.5) 以确保 TL(0)= T[0] 和 TL(R)=T[N-1]。
下图 说明了使用纹理过滤从 N=4 的一维纹理中实现 R=4 或 R=1 的表查找。

关于作者
Ken He 是 NVIDIA 企业级开发者社区经理 & 高级讲师,拥有多年的 GPU 和人工智能开发经验。自 2017 年加入 NVIDIA 开发者社区以来,完成过上百场培训,帮助上万个开发者了解人工智能和 GPU 编程开发。在计算机视觉,高性能计算领域完成过多个独立项目。并且,在机器人和无人机领域,有过丰富的研发经验。对于图像识别,目标的检测与跟踪完成过多种解决方案。曾经参与 GPU 版气象模式GRAPES,是其主要研发者。
审核编辑:郭婷
-
main函数返回值的认知2016-10-24 2236
-
可以使用OpenGL GL_TEXTURE_2D的NvIFR使用GL_TEXTURE_2D纹理吗?2018-09-26 3515
-
关于返回值类型为void的函数的返回值2021-05-18 3480
-
利用函数参数和返回值提高嵌入式软件质量2009-11-07 1004
-
WebApi之接口返回值的四种类型2017-11-27 14293
-
C语言函数返回1和返回0到底哪个好?2021-04-22 3353
-
C语言函数的返回值2022-08-31 2575
-
C语言程序开发中关于函数返回值的问题2022-09-06 1246
-
Rust代码启发之返回值异常错误处理2022-09-22 2701
-
return-函数的返回值是什么2023-02-23 2418
-
什么是函数的返回值?2023-04-04 6341
-
C语言中函数的返回值指向一个指针2023-04-26 3964
-
Python函数作为返回值2023-09-27 1588
-
ARM异常返回值的合法值有哪些?各返回值分别代表什么?2023-10-19 1655
-
C语言如何处理函数的返回值2025-01-16 767
全部0条评论

快来发表一下你的评论吧 !

