

多采样率数字滤波器的抽取和内插过程 多速率滤波器的Matlab实现
描述
一、关于多采样率数字滤波器
很明显从字面意思上可以理解,多采样率嘛,就是有多个采样率呗。前面所说的FIR,IIR滤波器都是只有一个采样频率,是固定不变的采样率,然而有些情况下需要不同采样频率下的信号,具体例子我也不解释了,我们大学课本上多速率数字信号处理这一章也都举了不少的例子。
按照传统的速率转换理论,我们要实现采样速率的转换,可以这样做,假如有一个有用的正弦波模拟信号,AD采样速率是f1,现在我需要用到的是采样频率是f2的信号,传统做法是将这个经过f1采样后的信号进行DA转换,再将转换后的模拟信号进行以f2采样频率的抽样,得到采样率为f2的数字信号,至此完成采样频率的转换
但是这样的做法不仅麻烦,而且处理不好的话会使信号受到损伤,所以这种思想就被淘汰了,现在我们用到的采样率转换的方法就是抽取与内插的思想。
二、抽取
先来总体来解释一下抽取的含义:前面不是说,一个有用的正弦波模拟信号经采样频率为f1的抽样信号抽样后得到了数字信号,很明显这个数字信号序列是在f1频率下得到的,现在,假如我隔几个点抽取一个信号,比如就是5吧,我隔5个点抽取一个信号,是不是就是相当于我采用了1/5倍f1的采样频率对模拟信号进行采样了?所以,抽取的过程就是降低抽样率的过程,但是我们知道,这是在时域的抽样,时域的抽样等于信号在频域波形的周期延拓,周期就是采样频率,所以,为了避免在频域发生频谱混叠,抽样定理也是我们要考虑的因素。
下面来具体来介绍
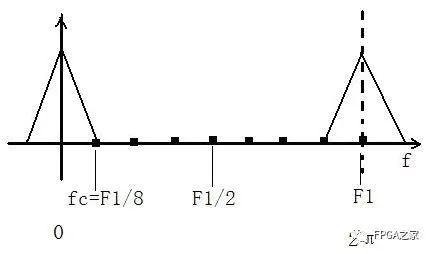
如上图所示,假如上面就是某一有用信号经采样频率f1抽样得到的频谱,假设这时候的采样频率为8Khz,可以通过数格子得到,从0到F1处有8个空格,每个空格代表1Khz,有些朋友可能会问,这不是在数字频域吗,单位不是π吗,哪来的hz?是的,这里是数字频域,采样频率F1处对应的是2π,这里只是为了好解释,我们用模拟频率来对应数字频率。
上面是采样频率为8K的数字信号频域图,现在我要对这个数字信号进行时域抽取,从而来降低信号的采样率,我们知道,一旦我们对数字信号进行时域抽取,那么采样率下降,而采样率就是数字信号频域的波形周期,那么也就是周期下降,所以,我们对信号进行抽取要有个度,要在满足抽样定理的条件下对信号进行抽取,否则就会发生频谱混叠。
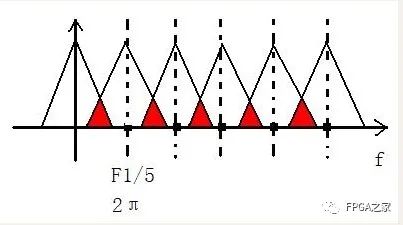
上图就是对信号进行了1/5倍的F1采样频率抽取,可见,由于发生了频谱混叠现象,因为1/5倍的F1是1600hz,而信号的频带是1000hz,不满足抽样定理,导致发生了频谱混叠,所以,为了避免发生这种情况,除了要满足抽样定理之外,即抽样倍数不能太高,我们还需要把信号的频带设置在F1/2以下,才能确保信号不发生频谱混叠,因此,我们需要在抽取之前加一个低通滤波器,书上叫做抗混叠低通滤波器,用来限制信号的频带,然后再进行抽取,这样的话我们来算一下
低通滤波器的截止频率就是1/2倍的经抽取后的采样速率,即fc = 1/2 * (F1/M) ,M是抽取倍数。而1/2*F1对应的数域频率是π,因此我们得出,
抗混叠低通滤波器的截止频率是π/M
三、内插
抽取的过程是降低采样率的过程,那么插值的过程当然就是提高采样率的过程。大体的思路可以这么理解,我们将经f1抽样下得到的数字信号的每两个点之间进行插值,插入的值是0,插值之后,信号在单位时间内的采样点数增多,当然也就是采样速率的提升,采样速率提升后我们知道,那么信号的频谱的周期就会增加。
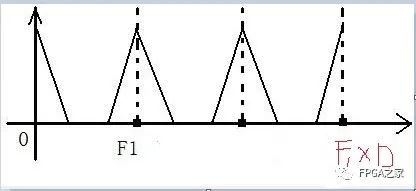
需要注意的一点就是,插值前后,我们只是在时域信号中间插入了D-1个零值,仅仅是改变了采样率,并没有改变信号的信息,因此,在频域,信号频谱的形状是不会改变的,改变的仅仅是周期,如上图,F1是插值之前信号的周期,插值之后,信号频谱的形状不变,周期成了F1*D,D是插值倍数。如果我们直接用F1*D倍的采样率采信号,得到的频谱会发现,就不会有中间两个波形,因此,这两个波形是多余的,书上叫做是镜像频谱。既然是多余的,我们就可以将它用一个低通滤波器滤掉,这样的低通滤波器,就叫做镜像低通滤波器。这样我们来计算一下镜像低通滤波器的截止频率。
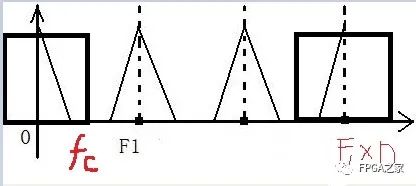
根据上面这张图我们可以求出镜像低通滤波器的截止频率,可以看到,fc = 1/2 *F1,这里我们假设,内插之后的采样频率为F2 =F1*D,那么,fc =1/2*(F2/D),而1/2*F2对应的是π,注意,这里是1/2*F2对应π,不是1/2*F1了,因为这已经是插值之后采样率增加之后的频谱了,所以我们得出:
镜像低通滤波器的截止频率为:π/D
四、 分数倍抽取与内插
根据前面抽取与内插的介绍我们知道了,内插的过程是先进行内插处理,再通过镜像低通滤波器,抽取的过程就是先进行抗混叠低通滤波,再进行抽取,我们可以看出来,假如我们想进行分数倍抽取,比如我要进行3/5倍抽取,就可以先进行3倍内插,再进行5倍抽取,这样就可以实现分数倍抽取。
再来看一下,当进行分数倍抽取与内插的时候,镜像低通滤波器和抗混叠低通滤波器是连在一起的,因此,我们可以将这两个滤波器合二为一,截止频率取两个滤波器截止频率的最小值就可以了
五、多速率滤波器的Matlab实现
这里我们假设,要对一个频率为100hz的正弦波模拟信号进行抽样,抽样频率为900hz,现在我要对采样信号进行5/3倍提升
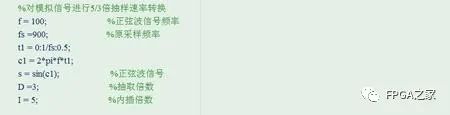
根据我们前面分析的,进行分数倍的抽样率转换,先要进行内插处理,内插的过程就是在原有的时域信号之间,插入I- 1个零值点,采用matlab实现很简单,首先我们可以计算插值完成之后信号的长度,然后将原来信号进行填充即可

插值完成之后,需要进行低通滤波,由前面的讨论可以知道,根据低通滤波器的截止频率计算公式,来计算滤波器截止频率为π/I,然后调用函数生成FIR滤波器系数即可。
紧接着,需要进行的是抽取处理,抽取过程的算法跟内插类似,可以先计算抽取之后的信号的长度,然后每个D个采样点进行一次抽取

下面看一张图,是我绘制了这个过程的整个流程
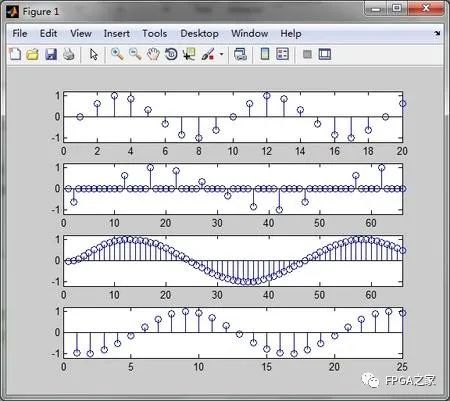
根据上面这张图我们可以看到,最上面的是原始信号经900hz频率采样后得到的信号时域波形,然后我对其进行了5倍内插,也就是在每两个采样点之间插入了4个零值,之后通过了低通滤波器,去掉镜像波形后的时域波形,可以看到,此时的采样率已经是原来的5倍,接着对其进行3倍抽取,即每隔两个点抽取一个点作为新的采样点,得到最下面的时域波形,整个过程原始信号没有发生变化,变化的仅仅是采样率。
六、关于CIC滤波器
说了这么多,终于进入正题了。前面的都是些基础知识,只有先掌握了前面的内容,才能理解下面的知识,包括下两篇文章要讲的FIR半带滤波器和多相结构的FIR半带滤波器。
CIC滤波器呢,是积分梳状滤波器的英文简称,先来看CIC滤波器的单位冲击响应
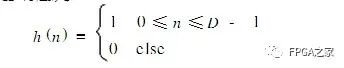
很明显的一个特征就是,CIC滤波器的单位脉冲响应只有0和1,再来想一下,既然单位脉冲响应只有0和1,那么也就是意味着,我们在进行卷积运算的时候,就不需要乘法器,为什么呢?因为滤波器系数为1的话,相当于将输入信号乘了个1,所以就不需要乘法器,只需要加法器就可以完成卷积运算,正因为如此,CIC滤波器结构简单,非常适合工作在高采样率条件下
但是这并不是我们常用的滤波器结构,既然是积分梳状滤波器,总得体现一下积分、和梳状这两个特点吧,这名字不是白叫的,因此有如下变形
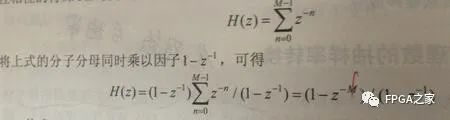
可以看到,上面的式子是CIC滤波器的系统函数,对其进行变换之后可以得到两个部分的乘积形式,即分子部分为一个梳状FIR滤波器,剩余部分为一个积分器,至此,我们CIC滤波器的结构才已经成型。
根据变形后的CIC滤波器的系统函数可以知道,滤波器的极点为1,因此看上去滤波器是一个不稳定的系统,但是从整体角度来看,这个结构是由一个FIR滤波器变形而来的,本身是一个因果稳定的,因此,变形后的系统应该也是一个因果稳定的,因此我们考虑到零极点抵消的原因,致使变形后的系统仍是一个因果稳定的系统。
从单级CIC滤波器的幅频响应考虑,由于其特殊的结构,导致单级CIC滤波器的衰减不足,可以见下图
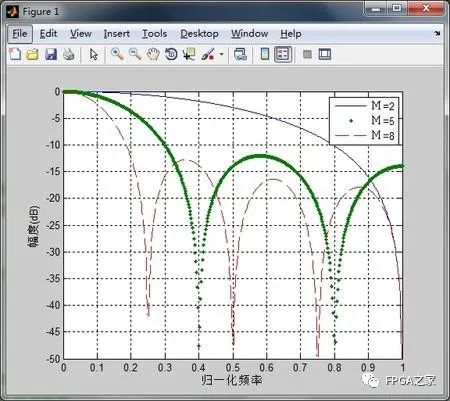
可见,单级CIC滤波器滤波器的衰减并不是很足,在阶数比较大的情况下,CIC滤波器的衰减一般稳定在13.6dB,要想加大衰减,就必须采用多级CIC滤波器级联的形式,每增加一级滤波器,阻带衰减增加13.6dB,但是为了增加阻带衰减而采用级联方式,也会导致一些弊端,为此,这方面的知识总结如下,具体理论不再解释了,书上的推导过程比较复杂,大家还是自己看书为好。
总结:
1、要同时满足通带容限跟阻带容限的误差的CIC滤波器实现起来比较困难,因为要想阻带衰减大,就要增大滤波器级数,但是会导致通带容限增大。
2、如果要实现这样的滤波器,只有当有用信号的频带相对于采样信号的速率很小时才能设计出符合要求的滤波器,这样的话通带衰减较大的情况下也对有用信号影响较小。
3、有用信号的频带相对于采样信号的速率很小也就是意味着信号的采样率很高,所以,CIC滤波器适合应用在多速率信号处理的前端,作为抗混叠滤波器来用,或者是作为后端的抗混叠插值滤波器。
七、多级 HogenauerCIC抽取滤波器的FPGA实现
HogenauerCIC抽取滤波器是一种特殊的结构,可以用来提高滤波器的运行速度,节省硬件资源等
前面已经说过了,CIC滤波器的系统函数经过变形之后,可以得到一个M阶的梳状滤波器和一个积分器相乘的形式,二者共同组成了抗混叠低通滤波器,在抽取的过程中,一般是信号先经过抗混叠低通滤波器进行滤波,来避免频谱混叠现象的发生,然后再进行抽取处理,但是我们可以利用Noble恒等式,先对信号进行抽取,再对其进行滤波,即
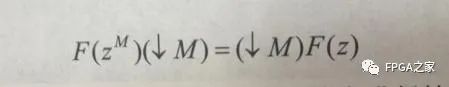
也就是说,在滤波器阶数跟抽取倍数相同的情况下,如果先滤波后抽取,那么滤波器的长度是M,但是如果先抽取后滤波,那么滤波器的长度就会降低为1阶,因此,采用Noble恒等式,先抽取后滤波,可以降低滤波器长度,从而达到节省硬件资源的目的。
前面说了,单级的CIC滤波器很难满足需求,要达到一定的阻带衰减,就必须通过级联的方式
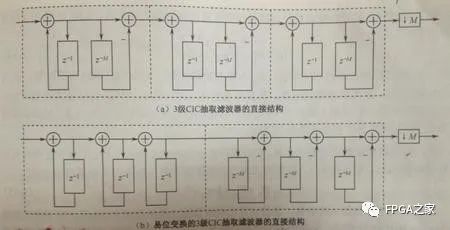
我们可以看到,如果是三级的CICI滤波器级联的话,也就是有3个积分器和三个梳状滤波器,这时候我们可以利用Noble恒等式进行移位变换,让积分器放在一起,梳状滤波器放在一起,这时候的梳状滤波器是M阶的,因为此时还没有经过抽取,所以我们可以再利用Noble恒等式,将抽取器放到梳状滤波器之前,这样的话,梳状滤波器就会降为1阶,长度为2,从而大大节省了硬件资源
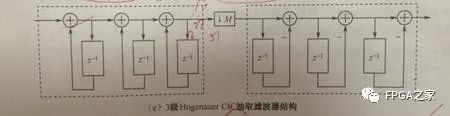
现在我们假设抽取倍数是5,根据要求,这时我们的滤波器长度也应该是5,采用3级CIC滤波器级联的方式,用HogenauerCIC抽取滤波器结构在FPGA上设计
1、三级积分器模块
altera 的CIC滤波器的IP核手册中给出了CIC滤波器中间运算数据字长的计算公式,这里我们假设我们的输入数据是经过10bit量化过的正弦波数字信号,那么CIC滤波器的中间运算字长为:
Wi = Win +N*log2(MD)
Win是输入字长为10,N为滤波器长度5,M为抽取倍数5,D位级联数3
因此算得CIC滤波器的中间字长为 Wi = 10 +5*log2(5*3) =30
知道了我们中间运算的字长就可以来设计我们的模块了,首先是积分器
积分器的设计比较简单,就是一个反馈回路,输出结果跟输入相加后延时一个时钟单元后再与输入相加

剩下两级积分器也是一样,第一级积分器的输出要送到第二级积分器的输入,代码这里不再列出,都是跟第一级积分器类似
2、五倍抽取器
抽取器的实现很简单,从积分器输出的数据,我们每隔5个数据抽取一个数据就好了

3、三级梳状滤波器
我们知道,经过抽取之后的梳状滤波器阶数降为1,长度为2的这样一个FIR滤波器,由于他的频谱很像一把梳子,因此得名为梳状滤波器。根据前面的变形后的公式,我们很容易得出,1阶梳状滤波器的单位脉冲响应为hn = 1 , -1,既然有了单位脉冲响应,我们做的就是一个简单的卷积运算就好了,而且这里的系数只有1和-1不需要乘法器,做一下加减法就好了

我们可以看到,跟之前做FIR滤波器一样,我们先把数据送到移位寄存器,因为1阶FIR滤波器只有两个系数,因此只要两个移位寄存器就够了。然后我们把系数跟输入的数据对应相乘,因为系数是1,所以乘法器就省略了,只需要做些加减运算就好了。
经过3级梳状滤波器滤波后的信号就是我们需要的信号了
然后是关于滤波器输出信号的数据截尾问题,我们可以通过matlab仿真,看一下输出数据的最大数据可以用多少位表示来确定输出数据位宽,如果不想做仿真的话,可以根据altera的CIC滤波器 的IP核手册中给出了CIC滤波器输出数据位宽计算公式来算:
即 Wo =Win +log2(N^D)
这里我算出来是17,因此,我们将梳状滤波器的输出值进行截低17位处理
仿真的过程我是采用 一个1khz和一个40khz的正弦波信号合成的,用采样频率为200Khz对其进行采样,按照我们上面的设计,滤波器的截止频率应该是
fc = 1/2 * (200 / 5) = 20Khz
所以经滤波器滤波后,40Khz的高频信号将会被滤掉,下面是仿真结果
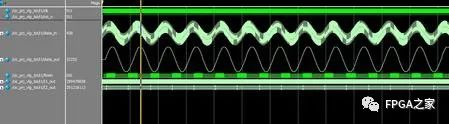
接着,我们将FPGA的输出信号读到matlab中进行仿真,绘出输出信号的时域波形
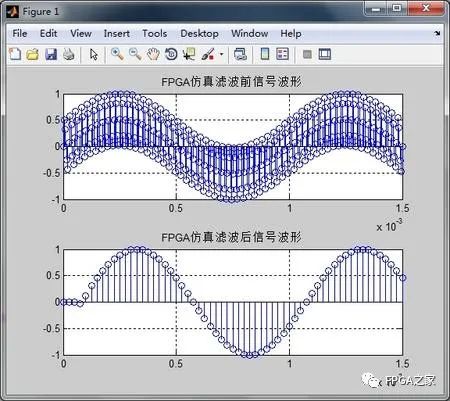
从这张图我们可以清楚的看到,上面的波形是滤波前的合成信号的波形,下面的是经过滤波后的波形,很明显,滤波前后,信号的频率没有发生改变,发生改变的是采样率,可以数一下,下面波形两点之间的距离,要比上面的信号宽4倍,也就是5倍抽取,仿真结果证明,我们的设计是正确的。
原文标题:CIC滤波器的FPGA实现
文章出处:【微信公众号:FPGA之家】欢迎添加关注!文章转载请注明出处。
审核编辑:汤梓红
-
请问AD7607内部数字滤波器的过采样率怎么理解?2023-12-06 578
-
数字滤波器的Matlab设计与应用2009-01-06 771
-
数字滤波器的MATLAB设计与DSP上的实现2009-04-16 820
-
数字滤波器的MATLAB 设计与DSP 上的实现2009-05-15 556
-
基于频率采样法FIR数字滤波器的设计2010-03-31 1220
-
数字滤波器的设计实验2008-10-30 6149
-
数字滤波器的MATLAB与DSP上设计实现2010-04-12 2133
-
多速率采样中的CIC滤波器设计与分析2011-09-20 1234
-
基于Matlab/Simulink的FIR数字滤波器的设计与实现2016-01-15 1145
-
基于matlab的数字滤波器的设计及数字滤波器基本结构2018-06-05 1964
-
基于LabVIEW的数字滤波器设计过程2019-09-14 12553
-
FIR数字滤波器设计2022-04-05 6508
-
数字滤波器是什么 数字滤波器的性能指标2023-02-24 6591
-
基于Matlab和DSP设计FIR数字滤波器方案2023-10-19 487
-
什么是数字滤波器的采样速率?和输入信号的频率有什么关系?2023-10-20 4355
全部0条评论

快来发表一下你的评论吧 !

