电容充电电路工作原理以及计算

一.前言

与纯电阻电路不同，具有电容的电路中的电压不会立即进入稳定状态。当我们把电压源施加到下图RC 电路中，然后当 S1闭合时，电容C两端的电压将从零以指数方式上升到最终值。在这种情况下，电路中的电流也呈指数衰减，直到电容器充满电时，其两端电压达到电源电压。电容上的电压和电流发生变化的情况被称为瞬态条件。电容在上电启动期间发生的瞬态变化是由于充电造成的。

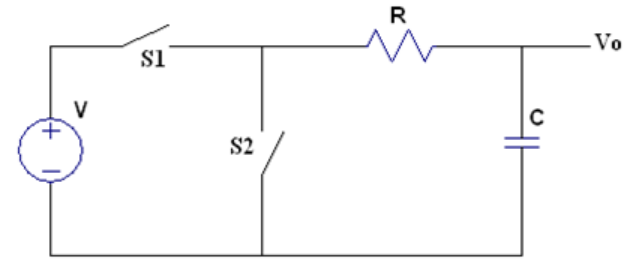
二.理论分析

电容在上电时导致的瞬态峰值电流非常高，这可能会损坏电路中的其他器件。当开关S1闭合时，瞬态电流与电容和电压变化率的乘积成正比：

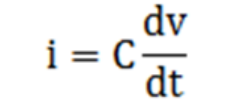
从公式可以看出，一旦电容两端施加的电压不再变化，电流i为零。所以一旦达到稳定阶段，电路中的电流由电阻R的阻值和电路的负载决定。

当S1闭合而S2保持打开时，电容将开始充电。在这种情况下，电阻和电容中的电流之和始终为零。这是由于两个电流之间存在180度的相位差。

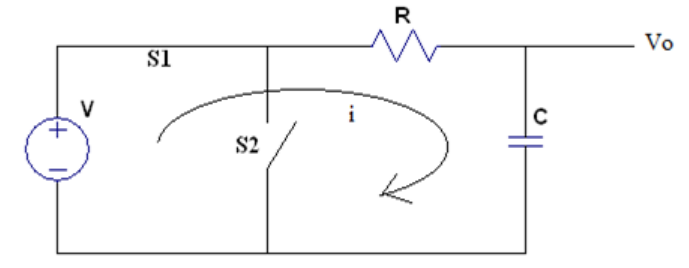
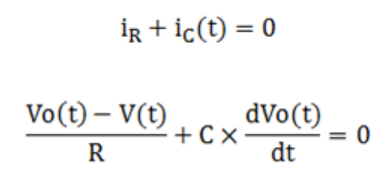
整合一下上面的公式可以得到：

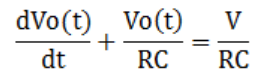
从而我们可以得到电容充电电压随时间的变化关系式：

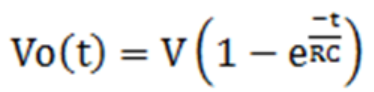
电阻两端的电压等于输入电压V减去电容C的电压：

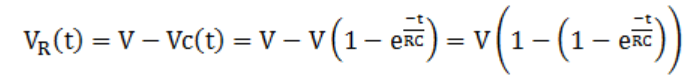
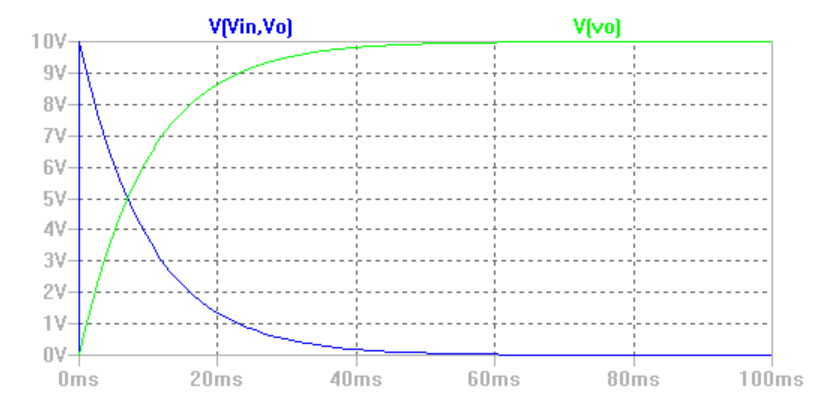
通过仿真软件，我们可以得到R和C上对应的各自电压的波形，绿色曲线是电容上的电压，而蓝色曲线是电阻上的电压的波形。电源电压设置为 10V，可以看出电容的电压一开始为零，然后以指数方式稳定到输入电压（此时电容器已充满电）。

 

三.RC常数

时间常数等于电阻R和电容C的乘积，代入一个时间常数可以得到充电电压值：

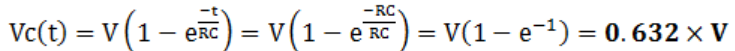
那么在5个时间常数可以得到充电电压值为：

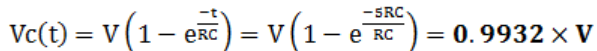
所以这里你就明白了为什么常说3-5RC时间段内电容电压就基本充满了，一般估算电容的充电时间用。