

使用光学传感器检测粒子
描述
光学传感技术是许多精密仪器和监视器的基础,因为它们是非破坏性和非侵入性的。随着集成光学传感器和光电容积脉搏波 (PPG) 模拟前端设备的普及,这些光学传感器也可以做得更紧凑,组件更少,功耗更低。
光学传感非常通用。光从光电发射器穿过感兴趣区域。光沿其光路与目标分析物相互作用,产生的辐射被光电探测器捕获。发射光和接收光之间的差异提供了关于检测区域中分析物的信息。
透射系统将接收器直接放置在发射光的路径中,而反射系统则依赖于反射或反向散射的光(图 1)。在实际应用中,容纳光电发射器和光电传感器的外壳材料也可以反射光,因此将光电检测器放置在与发射光成一定角度以减轻直接反射的干扰也是很常见的。大多数光在发射后沿其路径传播,看似不受影响,但一小部分会向各个方向散射,尽管各个方向的强度不同。无论发射器和传感器配置如何,在这种类型的光学传感中使用的原理都依赖于这种散射效应。
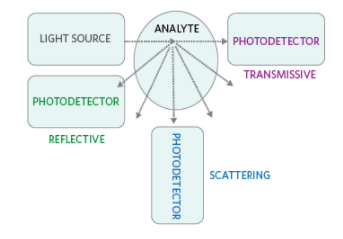
图 1. 如图所示,在光学传感中,发射光和接收光之间的差异提供了关于检测区域中分析物的数据。
说当光在其路径中“反弹”粒子时发生散射是不准确的。光是一种电磁波,它与某些分子中天然存在的电荷不平衡相互作用。这些电荷通过吸收进入的电磁辐射而被激发,然后重新发射。相互作用的结果取决于粒子的大小和光的颜色(波长)。
在讨论光束与沿其路径的粒子相互作用时的影响时,经常引用瑞利散射方程。瑞利方程如下:
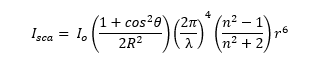
其中
I sca是角度 θ 处粒子处的散射光强度,
I o是发射光强度,
r是散射粒子主直径的一半,
n是光的折射(光速在真空除以材料中的光速),
R是粒子与光发射器之间的距离,
λ是发射光的波长。
为了简化讨论,我们可能只关注反向散射配置。在这种情况下,cos 2 θ = 1,反向散射光强度是粒径r和光波长 λ 的函数。设计者可能倾向于得出结论,可以通过用两种不同波长的光询问相同的粒子并捕获反向散射光强度来求解r的值。
虽然说明这个概念很有用,但情况要复杂得多。最重要的是,瑞利方程只有在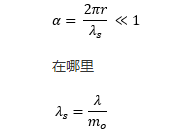
λ是发射光的波长, m o是周围介质的折射率,通常是空气。
红外 LED 光的常见波长约为 880 纳米,而许多灰尘或烟雾颗粒只有几微米。更完整的模型由 Mie 散射提出,适用于球形颗粒对光的吸收或散射,适用于不同粒径。不幸的是,米氏散射的数学方程要复杂得多。
考虑固定角度的微分散射光强度。散射材料的折射率 m 显着依赖于以下复数:

散射的相对幅度取决于折射率,而折射率又取决于构成散射粒子的材料。然而,一般而言,当我们保持所有其他因素不变时,我们可以确认,当粒子尺寸小于光的波长时,散射幅度较小,而当粒子尺寸大于波长时,散射幅度较大。
任何现实世界场景的复杂性使得建模结果先验不切实际。例如,
米氏理论仅限于球形颗粒,而真正的颗粒是不规则形状的
颗粒不会由均匀的材料或均匀的尺寸组成
为了克服这些复杂性,工程师们根据经验解决了一些粒子传感问题。通过用不同波长的光询问相同的粒子悬浮液,可以通过研究每个波长的散射光大小的差异来获取有关粒子的信息,同时保持其他一切不变。Mie 建议工程师必须仔细选择询问波长,因为折射率的差异会混淆差分散射幅度。成功实施的唯一方法是获取大量经验数据,并确保它们涵盖反映真实世界用例的反射粒子的所有合理一致性和构成。
审核编辑:郭婷
-
光学传感器的主要类型2023-07-18 2435
-
使用光学传感器检测颗粒2023-06-29 1257
-
光学心率传感器的工作原理2022-11-11 1303
-
光学传感器在电子应用中的作用2022-04-14 8638
-
如何利用光纤传感器来检测弧光事件?2021-05-19 2485
-
如何使用光学鼠标传感器实现旋转测量?2021-04-06 1752
-
FBG光学传感器的基本原理2020-04-30 2656
-
FBG光学传感器有什么优势?2019-11-06 3325
-
ROHM光学式表面贴装4方向检测传感器RPI-10402018-11-15 1688
-
ROHM超薄光学式4方向检测传感器RPI-10402018-10-30 1696
-
光学传感器的应用2018-09-18 17768
-
粒子计数器的一种新型光学传感器设计2018-02-09 1309
-
使用光学鼠标传感器实现旋转测量2015-07-30 6387
-
新型使用光学应变传感器2009-06-30 412
全部0条评论

快来发表一下你的评论吧 !

