机械按键硬件原理

1. 背景

1.1 机械按键硬件原理

机械按键是指在硬件电路中，通过机械按键开关实现电平信号的通断来达到按键触发的硬件组件，见图1.1:

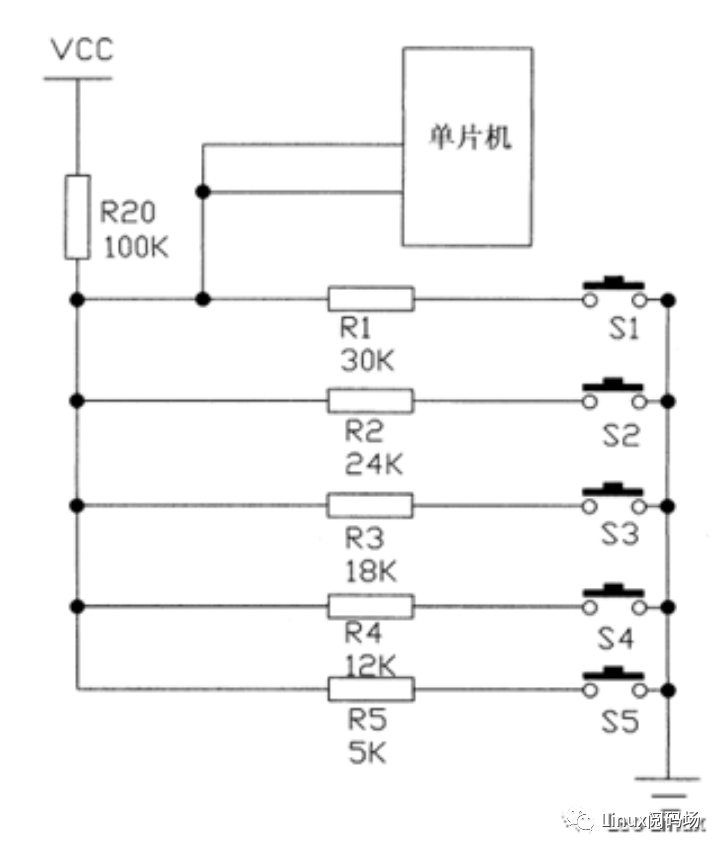
图1.1

嵌入式等电子设计中，机械按键的检测两种方法：

● 扫描检测：定时扫描IO口状态

● 中断检测：启用IO中断

  此后的内容都是围绕定时扫描IO口状态的方式展开的。

1.2 机械按键抖动

1.2.1 抖动原因

由于机械触点的弹性作用，一个按键开关在闭合时不会马上就稳定的接通，在断开时也不会一下子彻底断开，而是在闭合和断开的瞬间伴随了一连串的抖动。设按键时间为Ta，抖动时间Td，则Ta、Td的特性如下（见图1.2.1）：
● Ta≈100ms（最快50ms）；
● Td≈10ms；

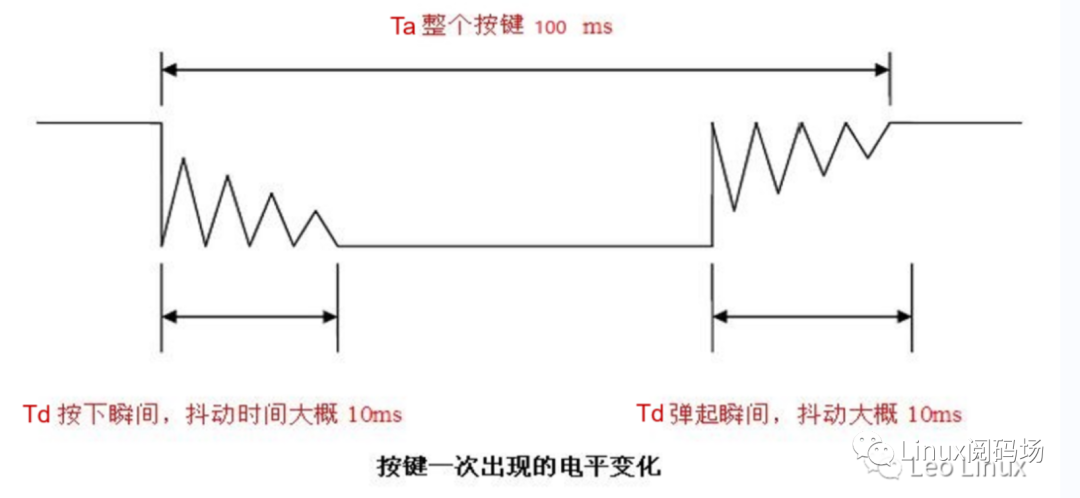
图1.2.1

1.2.2 按键消抖

理想的按键波形是没有抖动的，但实际的波形是有电平抖动的，对实际波形进行数字化抽象后会发现数字信号存在毛刺，见图1.2.2：

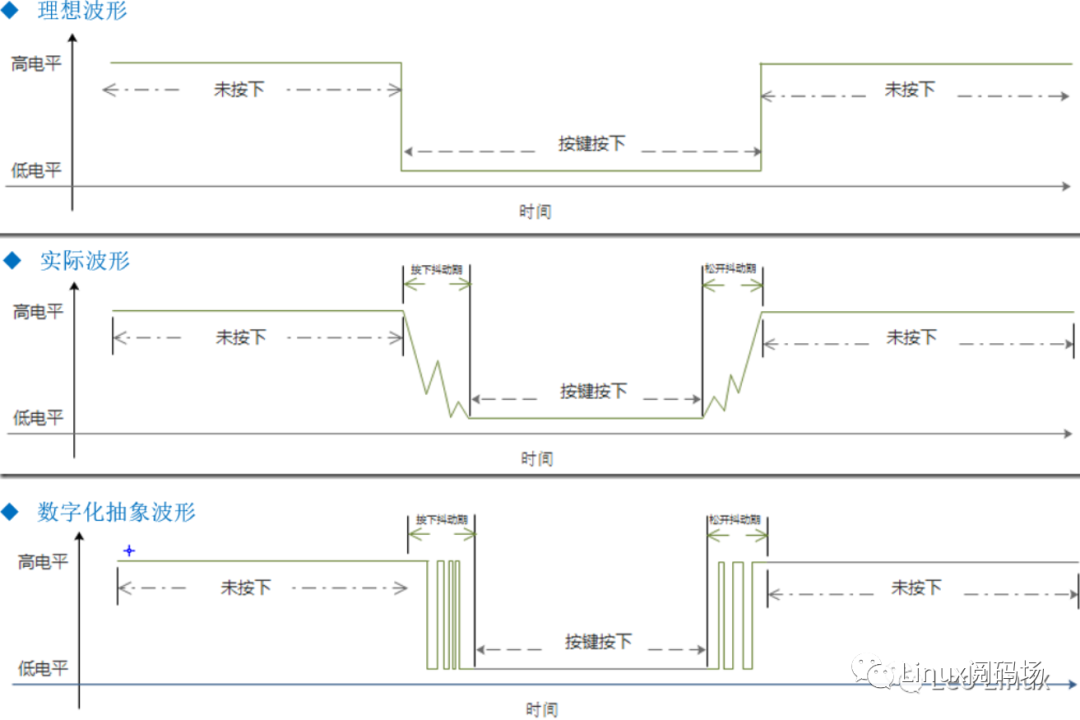
图1.2.2

为了消除电平信号的毛刺，目前工程上有两种手段，硬件消抖和软件消抖：

A. 硬件消抖

● 在硬件电路上和按键并联滤波电容

B. 软件消抖

● 延时确认：当检测到按键状态改变时，先延时20ms，再次检测按键；
● 持续采样：持续采集按键状态，用数字状态机逻辑来判断按键动作。

硬件消抖需要增加元器件，增加项目成本，软件消抖采用延时确认方式时，软件程序需要延时等待，延时过程不能进行其他处理，对程序架构不太友好，而持续采样不会对程序流程造成阻塞，后续对持续采样方式进行深入阐述。

2. 数字逻辑状态机的软件实现

2.1 抽象建模

2.1.1 按键操作状态抽象

一次按键动作可以抽象为3个状态，按下、抬起、长按：
● Keydown：一次按键操作的按下
● Keyup：一次按键操作的抬起
● Keypress：一次按键操作持续按住按键

 

图2.1.1

2.1.2 系统抽象

将软件扫描按键状态的软件系统进行数字逻辑电路抽象：
● 时钟抽象：软件每隔20ms采集一次按键的状态;
● 状态抽象：连续扫描3次得到状态序列011时，keydown才置1;
● 逻辑电路抽象：可以抽象为串行数据检测器，只有输入011才置1，采用同步时序逻辑电路的设计思路。

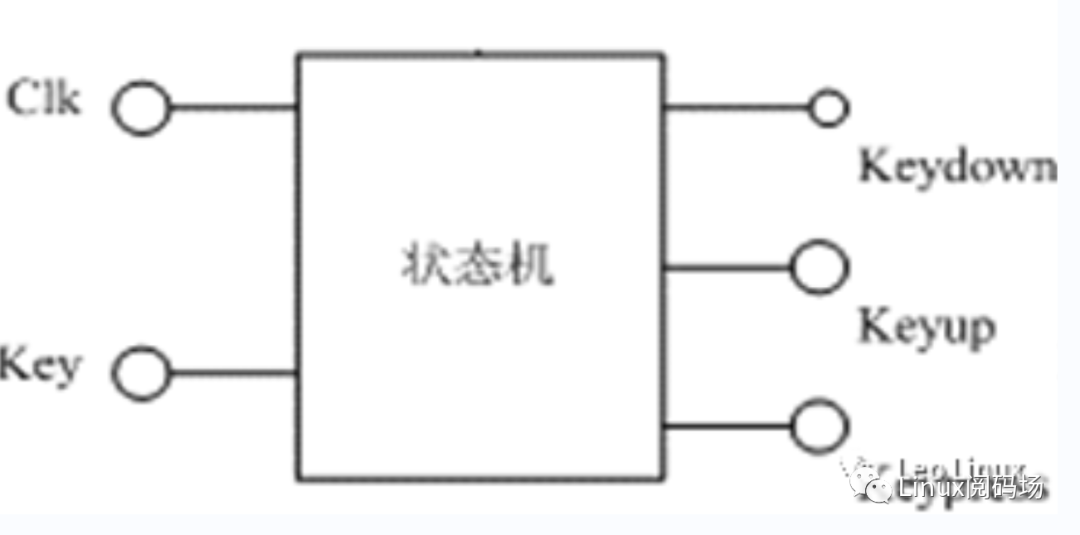
图2.1.2

2.2 数字逻辑算法实现

2.2.1 数字逻辑抽象

A. 变量定义

● Scankey：软件定时扫描的按键IO口状态（0/1);
● Keydown：一次按键操作的按下;

B. 状态逻辑抽象

● 设按键输入Scankey为X，输出结果Keydown为Y;
● 设没有1输入以前的状态为a;
● 设输入一个1后为状态为b;
● 设前后有两个1输入后状态为c;
● 设连续有三个1状态为d

C. 状态转换图

经过上面的数字逻辑抽象后，可以得到状态转换图和状态转换表：

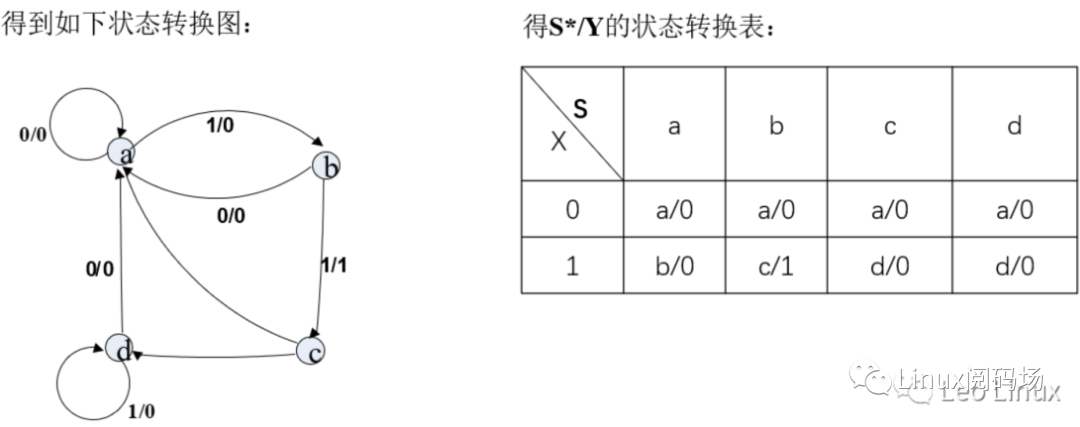
图2.2.1

2.2.2 求解过程

A. 化简状态转换图

通过上节的状态转换图和状态转换表（图2.2.1）可看出，状态c和状态d拥有相同的状态转换路径，所以可以将状态c和状态d合并为同一个状态c，化简后得到相应的状态转换图和状态转换表，见图2.2.2.A：

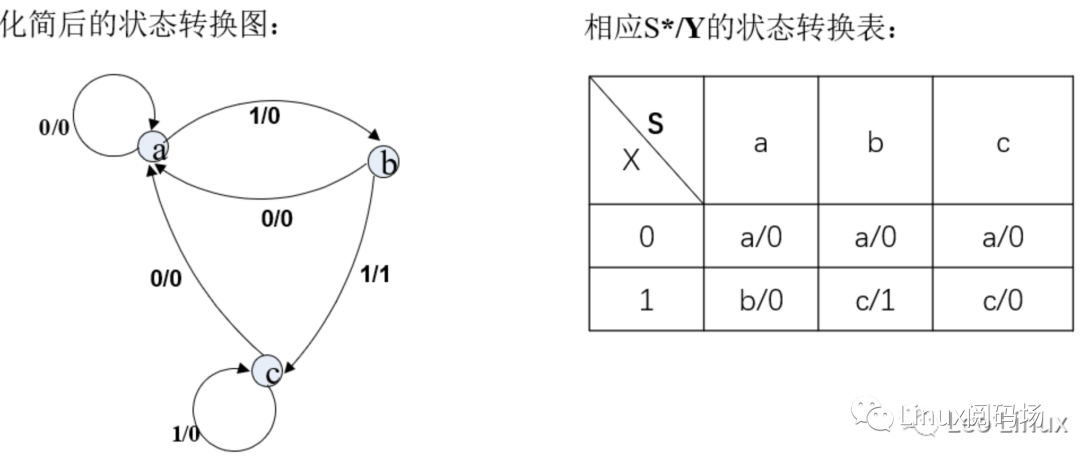
图2.2.2.A

B. 卡诺图

根据状态分配原则，状态M=3，所以取触发器位数n=2，可以选用两个D触发器：D0和D1，且输出为Q0、Q1。如果取Q1Q0的状态00、01、10分别代表状态a、b、c，依据状态转换图得到如下卡诺图。

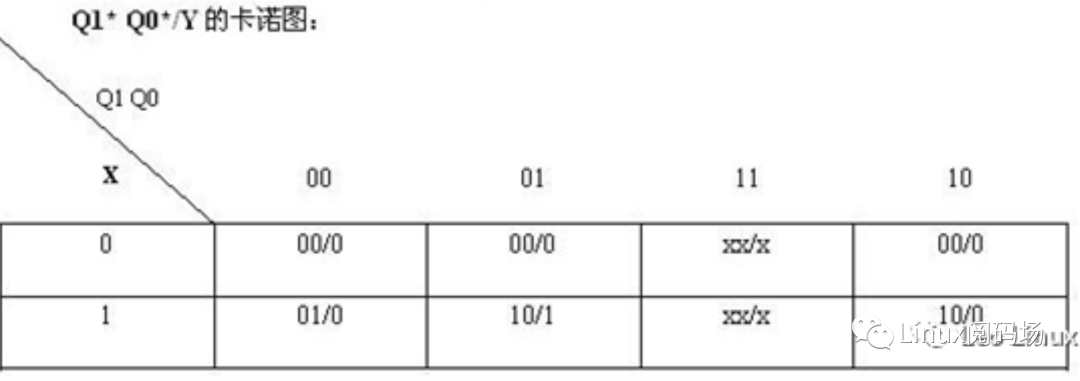
图2.2.2.B

C. 分解卡诺图

将卡诺图分解，得到图2.2.2.C：

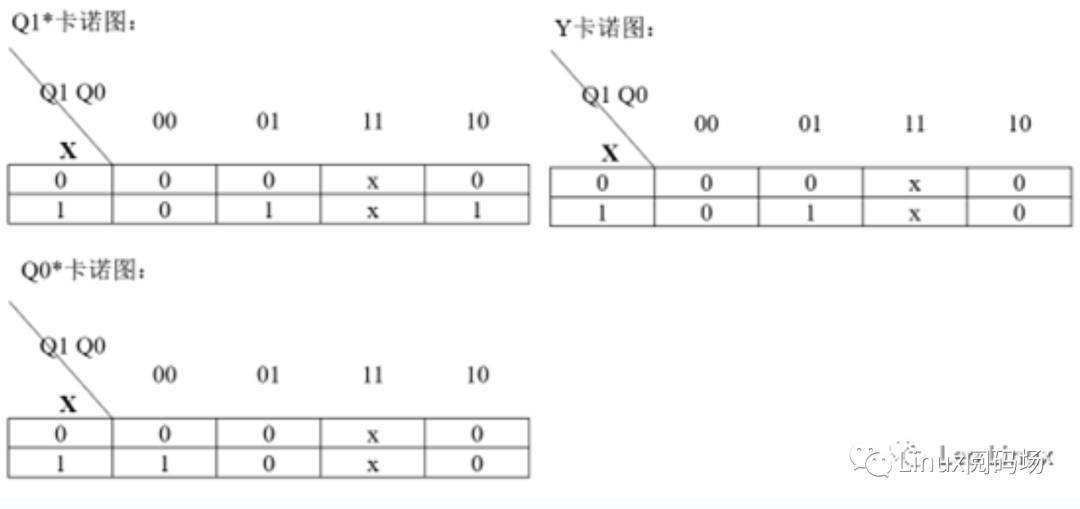
图2.2.2.C

D. 解方程

● 由Q1*、Q0*的卡诺图，可得状态方程：

 

Q1*=XQ0 +XQ1Q0*=XQ1ˊQ0ˊ

 

● 又因为D触发器特性方程为Q*=D，所以有：

 

Q0* = D0Q1* = D1

 

● 结合状态方程，得驱动方程：

 

D1 = XQ0 +XQ1D0 = XQ1ˊQ0ˊ

 

● 由Y的卡诺图得输出方程：

 

Y = XQ0

 

E. 转为C程序算法

定义每次扫描得到的按键电平信号状态的变量为Scankey，得按键按下Keydown相应C代码：

 

D1=Scankey & (Q0 | Q1); D0=Scankey & (~Q0) & (~Q1); Keydown=Scankey & Q0;Q1=D1;Q0=D0;

 

系统设计时申请一个时钟定时器资源，20sm触发一次，每次触发定时中断时扫描得到按键电平状态Scankey，并进行上述算法运算，得到Keydown状态，同理可推出Keyup和Keypress的算法，感兴趣者可自行推算。

3. 总结

上述数字状态机软件可以把一次按键操作的Keydown、Keyup、Keypress一起检出，代码精简，效率高。当然这种方式对系统实时性有要求，状态会随输入改变而改变，同时耗费系统定时器资源，需要定时查询。

审核编辑 ：李倩