如何在相控阵设计中应用优化技术

在本篇文章中，我们会展开一个适用于采用相控阵前端的雷达和无线系统应用的主题。 内容涵盖：

如何在相控阵设计中应用优化技术。

什么是二次规划？

在设计过程中采用优化解算器。

当设计大型相控阵系统时，这种优化工作流程可以节省大量时间，因为此过程会涉及很多设计参数，包括单个天线单元的位置和应用到每个天线单元的权重。因此，当从事电磁解算器层级的物理阵列设计工作以及系统层级阵列设计工作时，可以采用这些优化技术。

本文专注于系统级应用，同时我们在文章末尾提供了一个链接，通过其可以获取有关电磁解算器级应用的更多资源。

与单天线天线单元相比，相控阵的一个主要优点是可以形成一个波束（或多个波束），以增强所需的信号并降低干扰信号的影响。

通常，在合成一种方向图时，N 天线单元相控阵可提供 N 个自由度。这意味着可以调整N个权值，每个天线单元一个权值，以控制波束形状，从而满足一些预定义的约束。

正如在这篇博客（https://www.mwrf.com/technologies/systems/article/21849359/algorithms-to-antenna-synthesizing-an-antenna-array-with-optimization-techniques）中所述，可以采用各种技术来实现方向图合成，包括调零、加窗和稀布(Thinning)。应用优化技术有助于消除方向图合成时的“反复试错”过程。

许多常用的波束形成技术都可以表示为优化问题。例如，最小方差无失真响应（MVDR）波束形成器用于最大限度减小总噪声输出，同时保留给定方向的信号。我们之前在另一篇博客中介绍了此类波束形成器，但在数学上，通过解决优化问题即可得到MVDR波束形成权值。

在本文中，我们省略了数学运算，但是一个 N 天线单元阵列能够处理 N−1 个约束。MVDR 波束形成器可以进行扩展，以包含更多约束，从而成为线性约束最小方差（LCMV）波束形成器。LCMV 波束形成器中的附加约束常用于消除给定方向的干扰。

这些技术适用于任何阵列结构，但我们考虑一个包含 32 个天线单元、天线单元之间具有半波长间距的均匀线性阵列。我们可以采用 LCMV 方法执行阵列合成。我们的相关信号位于0度方位，干扰源位于 -70 度、-40 度和 -20 度方位。噪声功率假定比信号低 40 dB。图 1 显示了我们的方向图结果。此波束形成器可有效消除垂直虚线图中所示方向的噪声源。

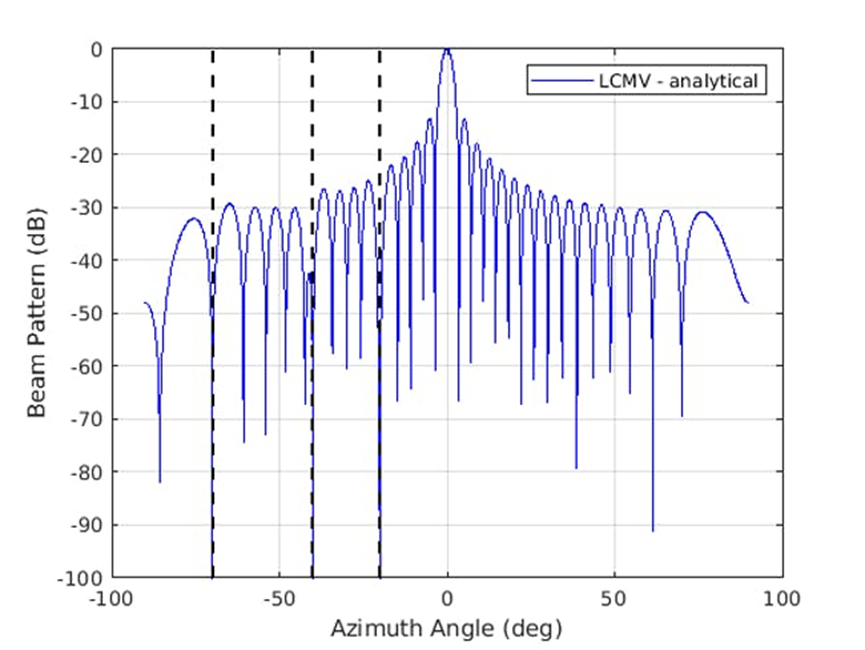
1.LCMV波束形成器用于消除干扰源。（2021 The MathWorks, Inc.）

MVDR 和 LCMV 算法的一个共同点是只处理等式约束。但是，方向图合成的另一常见要求是确保阵列响应一组给定的角度范围内低于某一阈值。例如，我们可以将以下要求添加到所需方向图中：

1.  在 −30 和 −10 度方位之间，旁瓣应低于 −40 dB。

2.  在主瓣以外的任何地方，旁瓣应低于 −20 dB。

图 2 阐述了我们将尝试实现的系统所需的方向图要求。

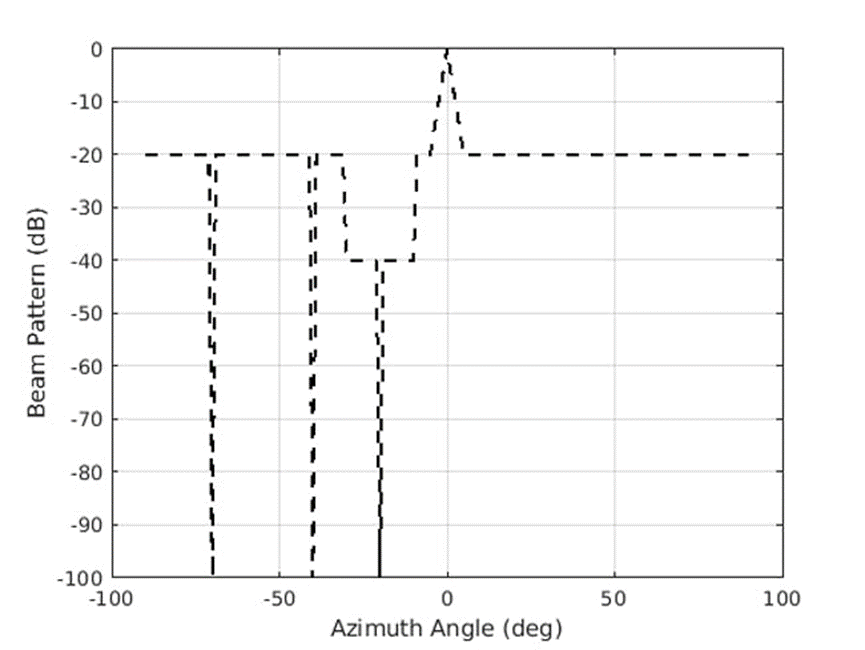
2.图示为阵列方向图的所需特性。（2021 The MathWorks, Inc.）

MVDR 和 LCMV 算法无法再用于解决此类问题，因此我们想介绍另一种涉及优化解算器的技术。

优化解算器用于最小化给定约束集下的目标函数。基于目标函数和约束条件，一些优化解算器比其他解算器更有效。因此，选择适合应用的优化解算器非常重要。

在本文中，由于目标函数旨在最大限度减小功率，所以很自然地将其视为二次规划（QP）问题。例如，可以使用优化工具箱中（https://www.mathworks.com/products/optimization.html）的 quadprog 函数。

尽管 QP 解算器似乎很适合我们的方向图合成问题，但是将阵列合成问题转化为 QP 公式并不简单。这是因为解算器通常处理实数，而阵列方向图计算会涉及复数。我们需要首先将复数运算转化为实数运算，形成目标函数和约束的实部和虚部，然后确立二次规划并使用解算器。

图 3 所示为使用合成权值产生的方向图。请注意重叠的虚线部分，这就是我们的所需要求。−70、−40 和−20 度方位均为零，并实现了新的旁瓣水平。

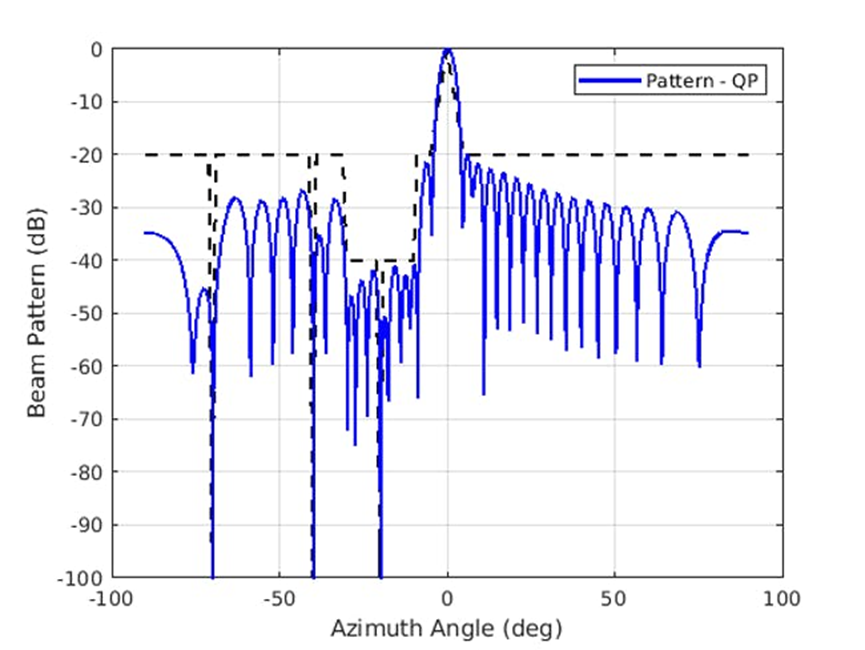
3.此合成方向图采用二次规划优化技术，满足了所需要求。（2021 The MathWorks, Inc.）

二次规划可以完成此项工作。但是，为了将复数约束转化为实数约束，我们不得不分别考虑实部和虚部，而在理论上，我们只需要确保两者的范数满足不等式。因此，在QP公式中，我们对波束方向图的实部和虚部采用更严格的约束。

另一种优化解算器称为二阶锥规划（SOCP），具有以范数形式定义的约束。此解算器可为解决我们的问题提供另一种可行的选择。

此外，由于我们方向图合成问题中的约束更自然地与 SOCP 公式相匹配，所以我们预计采用 SOCP 获得的结果可能优于通过QP获得的结果。

但是，即使 SOCP 问题的目标函数是线性函数而不是范数，也可以将包含范数的原目标函数转化为附加的二阶锥约束。然后，可以利用 SOCP 解决我们的最小方差方向图合成问题。

图 4 展示了采用优化工具箱中的 coneprog 函数实现的方向图。将此结果与通过 QP 得到的方向图进行比较，我们可以看到，SOCP 解算器达到了更低的旁瓣水平。

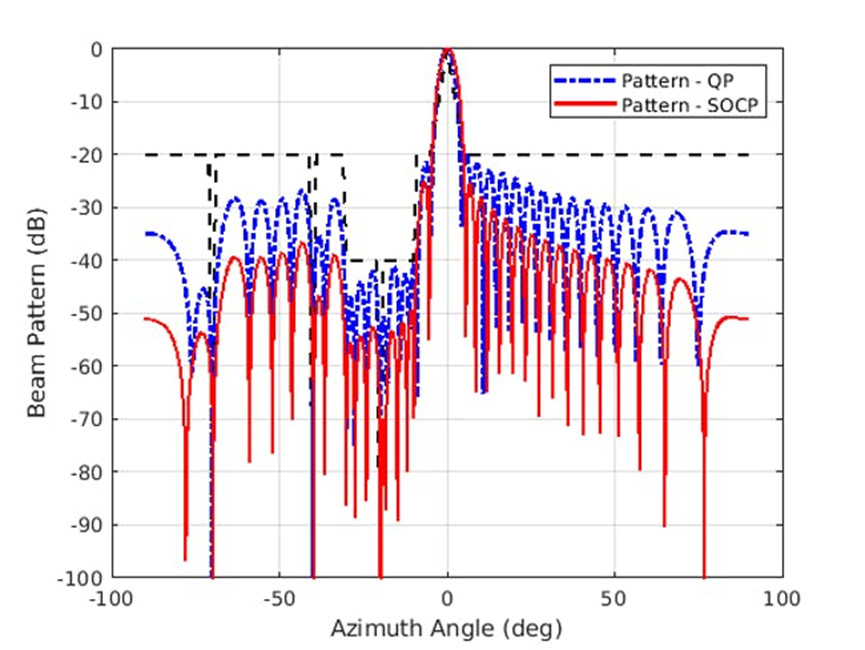
4.在这里，合成方向图采用二次规划优化技术，满足了所需要求，并与SOCP相比。（2021 The MathWorks, Inc.）您可以采用相控阵系统工具箱、天线工具箱和优化工具箱设计系统中的阵列。相控阵系统工具箱 https://www.mathworks.com/products/phased-array.html 天线工具箱 https://www.mathworks.com/products/antenna.html 优化工具箱 https://www.mathworks.com/products/optimization.html  

审核编辑 ：李倩