关于振荡器和晶体振荡器应用分析

　　频率基准需要振荡器。所有时钟都用于（微）处理器，但所有计时电路也需要一个时钟 。以晶体作为基准，可以获得了最高的精度；无需大量的努力，0.1%的精度就能轻易获得。这就是为什么我们从晶体振荡器开始这一章。结果表明，只需要一个晶体管就可以构造一个晶体振荡器。

　　在设计这个振荡器之前，我们必须回顾一下振荡的条件，之后我们来看看这种晶体的电气模型是什么；它现在可以用来构造一个具有最小功耗的单晶体管振荡器。MOST晶体管和双极晶体管都可以用来实现这种振荡器。最后，振荡的原理可以扩展到构造其他类型的振荡器，如压控振荡器 （ωoltage Controlled Oscillator， ωCO） 等。

　　振荡器原理

　　振荡器是一种反馈放大器，反馈的信号正是放大器维持振荡所需要的，它的输入现在为零。这被称为巴克豪森标准 （ Barkhausen Criterion ）。该放大器具有依赖于频率的增益A（jω），此外反馈块具有与频率相关的衰减F（jω）。环路增益F（jω）A（jω）必须足够大，以便反馈的信号vf完全等于ve，这是必需的。结果，环路增益在振幅上必须略大于单位增益，相位为零。

　　这意味着如果F（jω）是衰减器，则A（jω）必须是放大器；这也意味着如果A（jω）是电容性的，则F（jω）必须是电感性的。我们所见过的所有放大器都包含电容， 因此我们需要为Fjω） 找一个电感。显然，这两个条件是 A（jv） 和 F（jv） 的复数性质的结果， 复数总是成对的数字。

 

 

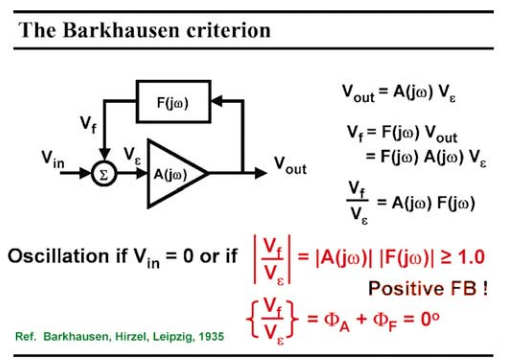
　　图 1 巴哈豪森 （ Barkhausen ） 振荡 （条件） 标准

　　另一种写巴哈豪森标准的方法是通过分裂分析给出的。放大器现在由阻抗Zcircuit表示，反馈元件由谐振器阻抗表示。由于电路自身可以保持振荡，因此不需要来自外部的电流；其总输入导纳量为零，阻抗的和也必须为零。巴克豪森标准现在可以用下图中的两个表达式来表示：现在使用的是实部和虚部，而不是幅度和相位，它们显然是相关的 。我们之后会看到，第一个表达式决定了所需的最小增益，另一个表达式决定了它的实际振荡频率。

 

 

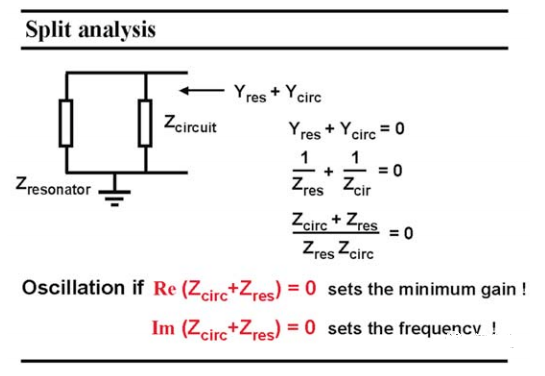
　　图 2 拆分分析

　　晶体振荡器

　　现在了解了振荡的条件，让我们找到电感来与电容放大器形成一个反馈环路，我们知道它们可以一起形成一个振荡器。我们使用的第一个电感是嵌入在晶体中的。

　　晶体是由具有一定厚度d的压阻材料板组成。压阻材料允许机械能和电能的交换。例如石英、氧化锌和一些氮化物。对其施加一个机械压力，会产生一个电压，反之亦然。这种能量交换在一个特定的频率上特别有效，这个频率称为谐振频率fs，其与石英的厚度成反比。通常会制作100kHz到40-50MHz的振荡值，对于较高的值，石英变得太薄和脆弱。

　　在这个谐振频率周围，该晶体的电气模型是一串联的谐振LRC电路，其谐振频率为fs。它受到串联电阻 Rs 的阻尼，从而导致品质因数 Q 是有限的。下图中给出了所有相关的表达。请注意，在谐振时，电感的阻抗等于电容的阻抗。实际上，在谐振时，串联 RLC 电路本身就是 Rs， 电感Ls和电容Cs相互抵消。除了代表晶体机电运行的这个串联 RLC 电路外，还必须添加一个平板电容 Cp。它是用于接触晶体的两块板之间的电容，具有石英的介电常数（比空气大 4.5 倍）。它还包括与封装有关的电容。

 

 

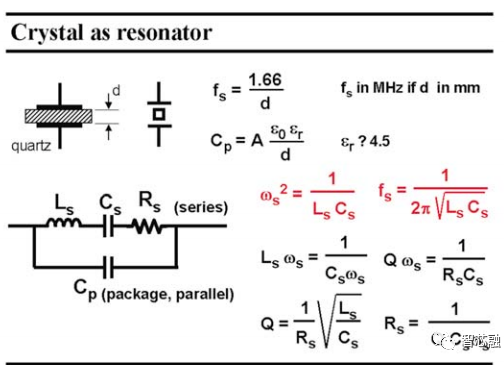
　　图 3 晶体作为谐振器

　　例如，10.00MHz的晶体可以用约10mH的电感，串联26fF的电容和 5Ω的阻尼电阻的串联LRC建模，注意电感相当大，电容非常小。一个经验法则说，它们大约是封装电容Cp的1/200到1/250。板式或封装式的电容总是在pF的数量级上，串联电容Cs始终在fF范围内。电阻非常小，因为质量系数Q很高，在105数量级左右！很明显，封装电容Cp与Ls也形成了一个并联谐振电路。我们同时有一个串联和一个并联的谐振电路！然而，我们尝试在串联谐振频率fs下制造一个振荡器，因为这是内部晶体频率，独立于封装或安装。

 

 

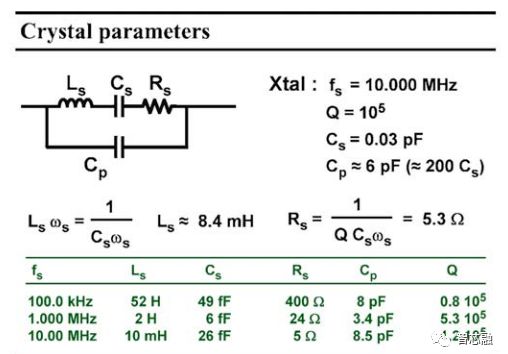
　　图 4 晶体参数

　　为了回忆起串联和并联振意味着什么，两者都绘制在下图。两者对谐振频率fr具有相同的表达式， 然而阻抗与频率的关系看起来非常不同：串联谐振电路的谐振处有明显的零，在谐振时，阻抗降低到电阻R， 晶体是纯电阻的；对于低于fr的频率，电容的阻抗增加，从而决定了电流，阻抗为电容性，相位为−90°。对于高于fr的频率，阻抗变为感性，其相位为 90°。

　　一个并联的谐振电路在谐振处有一个尖锐的峰值。在谐振时，阻抗受到电阻R的限制，晶体同样是纯电阻的。对于低于fr的频率，电感的阻抗减小，从而决定了电流。阻抗为感应的，相位为90°。对于较高的频率，阻抗变成电容性，其相位−为90°。这与串联谐振电路正好相反。

 

 

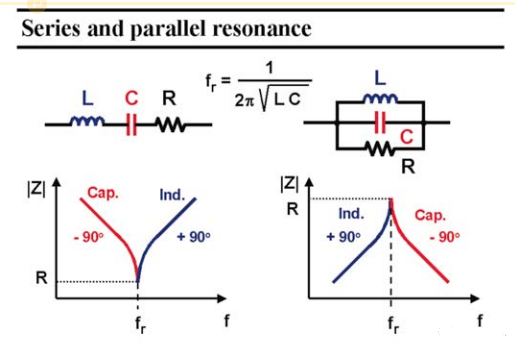
　　图 5 并联和串联谐振器

　　现在让我们回到晶体中，在下图中绘制出它的阻抗与频率。它用一个三阶表达式清楚地描述，如下图所示。一般来说，它显示了封装电容Cp的阻抗，它会随着频率的增加而减少。在谐振频率附近，我们注意到零点和峰值非常接近。零点在前，代表谐振频率为 fs 的串联谐振，而峰值代表并联谐振。现在我们把这个区域放大；

 

 

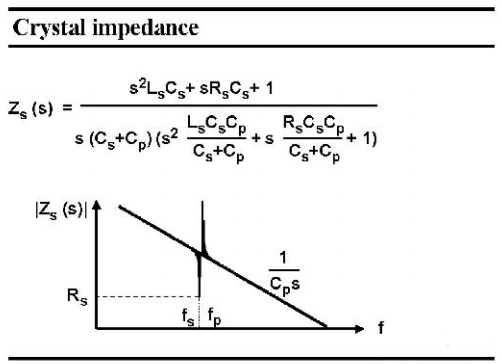
　　图 6 晶体的阻抗

　　现在谐振频率很容易区分，串联谐振频率fs是那个较小的。实际上已经计算出了给定晶体的值。下图上面显示了振幅，而底部的图显示了相位。如前所述，晶体在串联谐振频率 fs 的左侧和并联谐振频率 fp 的右侧充当电容。

　　然而，在两个谐振频率之间，晶体作为一个电感。由于质量系数很高，因此过渡幅度非常陡。该晶体现在作为从并联谐振频率fs到串联谐振频率fp的电感。我们使用这个电感和一个电容式放大器来制造一个振荡器。我们希望这个振荡器的工作在尽可能接近串联谐振频率fs，因为这是最接近晶体内部机电运行的频率。此外，这也是最不依赖于封装和安装电容的频率， 这些封装和安装电容难以预测。然而我们会看到，不可能在串联谐振频率fs下产生一个振荡器，这将需要无限的电流！然而，我们将尽可能的接近，这取决于允许使用的电流。

 

 

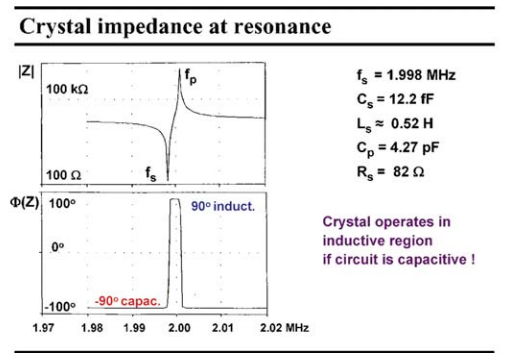
　　图 7 晶体在谐振时的阻抗

　　下面给出了串联谐振频率fs和并联谐振频率fp的实际表达式；串联的如下图中所述，另一方面，并联谐振频率fp由两个串联电容确定，通过检查模型可以清楚地看出。这个频率总是比串联的要大一些。如果我们发现Cp比Cs大了约200倍，那么 ωp2大约比 ωs2大0.5%。此外，ωp比 ωs大约0.25%。RLC串联电路的阻抗现在可以在下图中描述，在引入牵引因子 p 之后，我们将重写这个阻抗。这个牵引因子p是无量纲参数，它说明了实际工作频率距离串联谐振频率fs有多远。引入这个因子p和频率fs，给出了串联RLC电路阻抗的另一个表达式。据认为这个阻抗是电阻Rs和一个电感串联，这个电感越偏离串联谐振，就越大。我们将用这个简单模型来寻找振荡器的振荡条件。

 

 

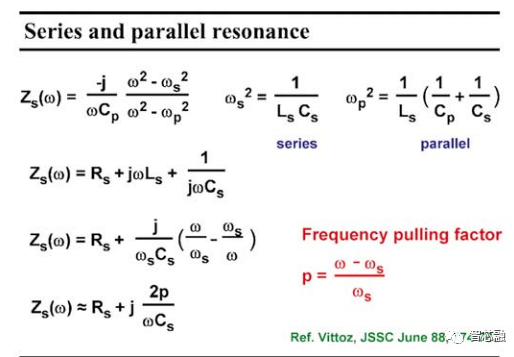
　　图 8 并联和串联谐振

　　术语串联或并联谐振通常归因于电路配置， 然而我们将会看到这是错误的！

　　串联和并联谐振只与振荡器的工作点有关。对于零或非常小的牵引因子p，工作点接近fs。在这种情况下，我们显然有一个串联振荡器；对于一个相当大的p，工作点接近fp，我们将其称为并联振荡器，虽然Cs在确定振荡频率方面的重要性仍然是Cp的200倍。中间的点是串联和并联谐振之间的交叉值fm。由于在fp时，牵引因子p约为0.25%，因此中间点的牵引因子一定约为其的一半或0.125%。我们现在可以得出结论，牵引因子p必须小于0.1% 左右，才能有一个具有良好的稳定性和可预测性的振荡器！

 

 

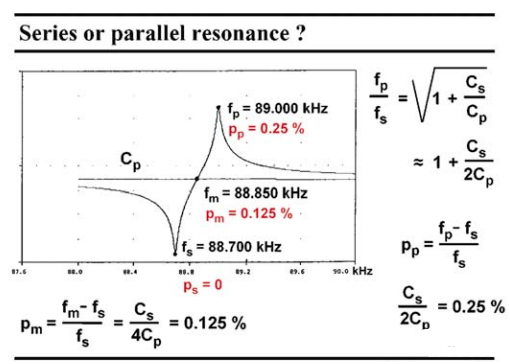
　　图 9 并联或串联谐振？