

关于架构师要找到“生产”好想法的方法
描述
引言
架构师的日常工作中,产生好的想法要占到我绝大多数精力。在两年前,我写过一篇《芯片架构方法学》的短文,目的是探索总结在芯片架构设计过程中,是不是有一些范式可以遵循,以提高过程中遇到的问题的解决速度。说白一点,就是能不能找到“灵感”发生的方法,进而用这个方法去生产方法。转眼两年又过去了,期间也一直在思考这个问题,偶有所得,跟大家聊聊。为了便于区别阅读,文中加粗字体的是2.0主要增改的内容。
第一篇: 回到定义
让我们先从一个小游戏开始,
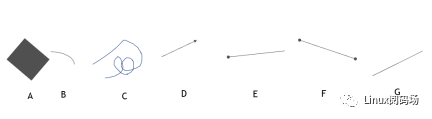
仔细观察上面的几个图形,其中哪些是直线呢?可能很多人会毫不犹豫的回答是”G”。其实,要回答这个问题,我们就要先弄清楚“直线”的定义,直线必须满足三个条件,第一,是直的;第二,是线,也就是必须是一维的,第三,直线没有端点。那么上面有哪个是同时满足这三个条件的图形呢?没有!A不是一维的,B/C不是直的,D/E/F有端点,G不是一维的,因为一维的直线是没有宽度的,而G之所以能够被我们人眼看到,说明它是有宽度的。
这里说这个小游戏的目的是为了引入一种非常重要的思维方式:回到定义。在我看来,我们平时遇到的很多问题,大部分可以通过“回到定义”来获得一个快速的模糊的答案。为了说明这种思维方式的强大之处,我们来看几个问题。
“这件衣服漂亮吗?”
“我做的饭好吃吗?”
“你觉得这个人勇敢吗?”
“你觉得这个事情好不好做?”
“这个解决方案的成本高不高?”
“这个方案和那个方案,哪个好?”
“从这里去公司,开车快还是做地铁快?”
“……”
无论是生活还是工作当中,我们无时无刻都会面临上面类似的问题,这些问题可能来自家人,可能来自同事,也可能来自路人。要回答这些问题,同样,也可以使用“回到定义”的思维方式,当我们弄明白定义之后,以上问题就迎刃而解了。
“什么是漂亮?”
“什么是好吃?”
“怎么定义勇敢?”
“怎么定义好做?”
“成本怎么定义?”
“怎么定义方案的好坏?”
“怎么定义快?”
你会发现,如果我们搞清楚了这几个定义,其实那些问题也就自有答案了。
我们平时的工作,其本质是选择,即,每时每刻要做出有利的选择。针对芯片行业来说,可具体化为我们要选择性能高(P),功耗低(P),面积小(A),复杂度低(C)的方案。一般情况下,大家在这个目标上是没有分歧的,分歧的产生在于每个人对PPAC的预估值不同,或者在于每个人所站的角度不同。然而,一个方案的好坏不止PPAC这四个指标,还有很多其它的参数,有时候也需要考虑进去。还有,上面的提到的“有利的选择”,对不同的人的含义也可能是不同的。最后,以上讨论大多都是基于人是理性的这个假设,然而事实并非如此,这就使事情变得越来越复杂,难以有显而易见的结论。
大道至简,面对这纷繁复杂的多彩世界,我认为“回到定义”是我们可以利用的一把利器,“回到定义”一般不是为了解决某个问题,而是过滤那些价值不大的问题。
关于“回到定义”,从另外一个角度看,可以理解为“第一性原理”,比如,我们要解决某个问题,这个问题的答案往往就藏在问题本身。比如,芯片架构设计中经常面临的问题:“如何提高芯片的power efficiency”,解决这个问题,我们就可以尝试以“回到定义”的方式来探索。
首先,我们可以提问:power是什么?或者说power都有哪几部分组成?这个问题不难。Power一般可分为static power和dynamic power。继续“回到定义”,static power主要是leakage power,继续“回到定义”,根据MOS结构,leakage power包含Drain->Well, Gate->Well,Source->Drain三部分。从前端设计的角度来看,这三部分主要受cell数量影响较大,所以,我们就可以尝试减少area来减少power。然后,我们根据“排列组合”思路,继续看dynamic power,再次“回到定义”,dynamic power=α·C · f · V^2
按照“排列组合”的思路,我们可以尝试降低α、C、f、V。这里我们着重看一下f和V。直接降低freq,一般perf会成比例的降低,但有的时候不一定,比如,freq的降低,意味着clock period的增加,即,时序约束的放松,而时序约束的放松,一般会伴随着area的降低,当area降低的程度超过perf降低的程度时(类比香农第三定理),就可以采用降低freq的方式提高power efficiency。此外,我们可以将“freq”的本意做一些引申,比如freq可以认为是data reuse frequency,这样一想,我们就可以尝试从算法,memory hierarchy等角度,提高data reuse rate,以降低“freq”,进而达到降低power的目的。我们再继续看“Voltage”,可以通过采用更先进的process来降低Voltage,进而降低power。关于Voltage,这里有个细节,实际上,dynamic switch power的产生,主要是因为表示“0、1”逻辑的电压差导致的,所以,从这个意义上讲,借用物理学名词,我们真正想降低的不是“绝对速度”,而是“相对速度”。
我们继续“回到定义”,dynamic power一般包含clock tree、mission function。所以做clock gating和data gating是降低power的非常重要的方法。当然,这里我们可以考虑“第一性原理”,能不能直接把clock tree去掉呢?因为clock tree去掉之后,自然也就不存在clock tree power了。答案是可以,即异步电路。
我们继续“回到定义”,mission function上的power难道就是我们必须要买单的power吗?不是,因为glitch power就不是我们愿意付出的power代价。所以,我们可以尝试降低glitch来降低power消耗,比如采用gray-code,调整clock skew。
我们已经“回到定义”很多次了,还可以继续“回到定义”。。。
上面我们通过一个小例子,展示了“回到定义”这种思路的能力。我想表达的是,在具体的芯片设计过程中,遇到问题时,如果一时难以解决,可以尝试“回到定义”,从问题本身寻找答案。
第二篇: 排列组合
排列组合的本质是降维。
面对一个复杂的问题,当这个问题的复杂性已经超出我们解决问题的能力时,就会变得很棘手。一般情况下,出现这种情况是因为这个问题的维度超过了我们认知的维度,这时,我们可以采用“排列组合”的思维方式来尝试解决。
比如“如何设计一个AI加速器”,这是一个很大的问题,我们可能很难在短时间内得到答案,因为这个问题的复杂性已经超出了很多人的认知范围。这时,我们可以将这个问题进行降维处理,变成多个较简单的,维度低一些的子问题:
“如何设计AI加速器的memory hierarchy?”
“如何设计AI加速器的data path?”
“如何设计AI加速器的control path?”
“如何设计AI加速器的运算单元?”
“如何使以上几个子系统协同工作?”
我们仔细观察发现,以上几个问题是最开始问题的子问题,以及这些子问题之间的关系的问题。也就是原始的问题被降低到了更低的维度。如果发现个别子问题仍然不能解决,那么,可以采用同样的方式,将这个子问题采用“排列组合”进行拆解。这里,我们假设“如何设计AI加速器的运算单元”这个子问题还是太复杂,超出了我们的能力,那么,我们可以进一步将其降维:
“如何设计AI加速器的Tensor processor?”
“如何设计AI加速器的Vector processor?”
“如何设计AI加速器的Scaler processor?”
同样,我们也可以继续拆解:“如何设计AI加速器的Tensor processor?”
“AI加速器的Tensor processor 负责完成哪些功能?”
“AI加速器的Tensor processor 的sequence如何选择?”
“AI加速器的Tensor processor PPA budget是怎样的?”
“AI加速器的Tensor processor 带宽需求是怎样的?”
“AI加速器的Tensor processor 需要的data format是怎样的?”
“……”
每个人解决问题的能力不同,所需要拆解到的问题的维度也不同,能力强的人,需要拆解的层数少一些,能力弱一些的人,可能需要将问题拆解到较低的维度时才能解决。
排列组合,除了可以将问题降维之外,还可以弥补脑容量不足所带来的问题。平时工作当中,有一类问题难度太高,一时无法下手,可以采用排列组合来解决,正如上面刚刚提到的例子;还有另外一类问题,其本身难度并不高,在我们解决问题能力范围之内,但问题比较繁杂,怎奈脑容量有限,一时难以将所有情况都考虑周全。对于这样的问题,也可以采用“排列组合”来防止遗漏。这个时候,“好记性不如烂笔头”就会发挥作用,当我们列出所有排列组合之后,然后用大脑依次分析,就能得出结论了。
上面最开始提到“排列组合的本质是降维”,降维,即,将问题拆解,是解决问题重要的手段。从相反的方向看,“排列组合的本质也可以是升维”。我发现“升维”竟然也可能利于问题的解决。比如,我们在武侠电影里经常看到以下场景。两个武侠高手最开始在地上打几个回合,几个回合过后,如果胜负未分,就会跳到房顶上,或者飞在空中,继续打。此外,我们也知道,在战争中,制空权一旦丧失,地面部队会变得非常被动。还有,在芯片封装时,如果芯片面积太大,可以做多层mask,甚至用3D stacking。我们发现,“飞到空中”、“制空权”、“3D stacking”的共同点是提高了问题解决的维度。在芯片架构时,这种思路有的时候也非常有用。比如,我们遇到一个问题,这个问题长时间都没有解决,采用“排列组合”的降维方式,发现tradeoff的点非常难受,顾此失彼,按下葫芦浮起瓢。如果面临这种情况,很可能是在目前的维度上,已经不存在明显的矛盾,真正的矛盾已经转移到了更高的维度上。这个时候,我们可以尝试“升维”,比如前面提到的clock treepower优化问题,如果我们已经采用了很多方法来降低clock tree power,但是距离目标还是很远,这个时候,去掉clock 就是一种升维,跳出原来优化clock tree power的维度,“飞到空中”。从这个角度看,当“山重水复疑无路”时,采用“升维”,说不定可以“柳暗花明又一村”。
这里需要澄清的是,“升维”不一定是维度的增加,也可以是维度的转换。比如,问题如果在空间上难以解决,就可以考虑将问题在时间上解决,反之亦然。比如,我们可以通过增加area来解决timing问题,也可以通过增加timing来解决area问题,可以通过增加area来降低power,也可以牺牲power来节省area,总之,PPAC四个维度都可以相互转换,就好像,area和M对应,timing和C对应,而power,很显然可以和E对应。
第三篇论数据
当今时代是一个信息爆炸的时代,天量的数据无时无刻的被生产,收集,传播开来,数据分析与筛选技能已经是一个人最基本的技能之一了,经过常年的学习与训练,关于数据的能力很多都已经变成了我们的前意识记忆,甚至是在非意识范围内影响着我们。这一点对于IT从业者尤其明显,在平时的工作中,无论是谁,每天都会面临很多“选择题”,而我们要做出选择,大多是出于理性的,而理性本身需要数据支撑。
“为什么采用这个方案,有什么好处吗?”
“这个方案的PPAC怎么样?”
“如果采用这个方案,会有什么代价?”
“……”
在做出以上选择之前,大多需要准备一些数据,而一个没有任何数据支撑的问题的决定能力是一个人重要的技能,对两个或者多个方案,数据上难分伯仲时的决策能力也是一个人重要的技能。
另外,数据有结论之前的数据和结论之后的数据之分。前者使我们自信,后者使我们开心。全面的数据使我们柳暗花明又一村,走出泥潭,片面的数据使我们不识庐山真面目,误入歧途。“实事求是,不先入为主”是SOL, “求全责备,所有决定都要有数据支撑”也是SOL,需要知道的是SOL我们人类做不到的。
给纷繁的世界建模以获取数据是困难的,在天量的数据中做出正确的决定也是不易的。数据不会骗人,骗人的是使用数据的人而已。我建议的是,工作中80%的决定要基于收集到的数据,20%的决定要基于内心。生活中20%的决定要基于收集到的数据,80%的决定要基于内心。类似模拟退火。理性是可贵的,但感性也不是一文不值。智慧是好的,但我们也不能倚靠自己的聪明。追求完美,大多数情况是褒义词,但有时候也可以是贬义词。
第四篇正反合(A=A=!A)
A=A=!A这个式子可以先拆成两个简单一点的式子来看:
A=A 和A=!A,为了便于描述,我称第一个式子为“A向左运动”,第二个叫“A向右运动”。
无论是在工作还是在生活中,我们的核心工作就是解决这样或那样的问题。以上提到的几种方法之所以有用,很大程度上是因为我们发现了问题的矛盾点。如果把“A向左运动”看成是“证明方案A是对的(矛)”的话,那么“A向右运动”就是“证明方案A是错的(盾)”。矛与盾相互否定,推动盾与矛互相肯定,这个过程反复出现,实现了问题的瓦解,即,问题的解决,达到了新的稳态,新的合理,新的存在。
比如,我们要新加一个具体的feature,最开始,我们会提出一个方案,假设就叫方案A,方案A的提出过程,其实就是“A向左运动”,这个过程中,最重要的是要确定“方案A确实可以解决这个问题”,就是A的肯定。一旦方案A提出之后,随之而来的是“为什么方案A有这个缺点”或者“为什么不选择方案B”,这个过程就是“A向右运动”的过程,即方案A的否定。接下来,就又是“A的肯定”过程,即,要完善最开始的方案A,完善之后可能还有反对者提出问题,如此往复,经过几个回合的拉锯之后,方案A渐趋成熟,而这时方案A还是方案A,方案A也是方案A的否定了。“追求无我,成就自我”,“无知者是不自由的”,每一次的否定自我,就是一次自我的肯定,每一次的自我肯定,都是向对立陌生的一次前进。
A=A=!A就是“正”,“反”,过程是螺旋上升的,目的是“合”。然而,世界是复杂的,我们偶尔也会遇到一时没有矛盾,但仍然需要我们解决的问题,这个时候,用我们人类最柔软的内心与这个问题握手。
第五篇 虚与实
相对于上一版,本篇的虚与实是新加的内容。
经过观察,我发现很多工程师,包括我自己在内,有的时候,在遇到问题后,最开始,第一步,就是尝试各种方法,我称之为“试错调试法”,期望通过多次的尝试,只要syndrome is gone,就算问题解决了。在解决比较简单的问题时,这种方法或许会奏效,但如果要解决比较困难的问题,“试错调试法”的效率就可能变得很低,这个时候我们该怎么办呢?我感觉,可以分成以下几个阶段:
Problem->modeling->SOL(First-principles)->reference->actual/solution->correction
首先,我们要认清问题,即,我们要先定义问题(problem definition),所谓“知己知彼”中的“知彼”。
在认清问题后,我们要对这个问题建模(modeling),最好用抽象的数学模型。
确定好数学模型之后,我们就可以求解这个模型,得到理想解,这里称为SOL(speed of light),这个理想解是尽量不考虑边界条件下的解。最好从前面我们提到的“第一性原理”出发。这个理想解非常重要,类似于我们的“希望”,设想,在没有希望的情况下工作,会是多么的不安。
理想是美好的,现实可能是残酷的。在拥有理想解之后,下一步,我们要低头看看,面对现实。这个阶段,可以查一些资料,看看已有的解决方案,分析自己的实际,即,边界条件,或约束条件。
理想与现实都有之后,我们就可以坐下来,考虑制定从现实到理想的行进路径,提出当前状况下的解决方案(solution)。
最开始的solution不用完美,根据前面提到的“正反合”思路,不断迭代,优化,即自我修正(correction),在修正的时候,就会再次发现新的problem。对于新的problem,从第一步开始。
这样就形成了问题解决的闭环。仔细观察,上面几个阶段是虚实交替的。类似于真空的磁场与电场,相互激发,共同传播,与光同行。
这里想着重提一下“SOL”,先抬头看天,再低头看路,要过有“希望”的日子。比如,我们IT领域,处理的是各种各样的数据,其中,数据的压缩,是非常常见的,普遍使用的技术,那么,给定一段数据,假设压缩方法不限(无损压缩),那么有没有一个理论上的最小值?如果有,我们压缩之后的最小数据量是多少呢?其实,答案是Yes,这个最小值可以通过香农定理给出:
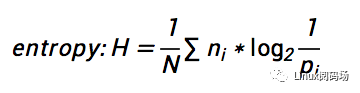
一旦知道了这个理论下限,我们就有了希望,有了开始的希望,也有了结束的希望。
有意思的是,这个定理可以给我们很多启示。比如,我们经常说的“信息”是什么?从定理中可以看出,“信息”可以理解为“概率”,并且概率越小,信息量越大。即,一成不变的东西,本身没有任何信息,因为其,简单计算可知H=0。进而说明,“千篇一律”,“人云亦云”等,并不会增加这个世界的熵,世界需要“鹤立鸡群” 、“一鸣惊人”。
番外篇 关于芯片架构
以上讨论了几种个人解决实际问题的方式方法,接下来说一下对芯片架构工作的体会。
芯片架构,大体上可分为三个事情:Architecture, Algorithm和Association。显然,架构工作,是要生产一些架构(Architecture)作为产品的,作为设计人员的参考与指导。架构本身并不是无根之木,是需要一些数据支撑的,而这数据的来源,主要是算法分析,所以架构工作还应包括一些算法分析的内容,此外,为了发挥所做架构的效力,应该提供一些基本的工具来帮助用户。三者之间,相辅相成,不同阶段,不同情况,重要程度不同。算法分析者可以提供必要的信息,比如算法发展趋势,所关心领域算法特点等重要内容,架构者基于这些内容,可以提出合适的硬件架构来,而另外一些人可以提供合适的工具来弥补架构和客户之间的gap。三者之间不是单向影响的,是互相关联的,架构者可以提出在做架构时的痛点,以影响算法发展和工具提供者。
芯片架构工作,很像是玩打地鼠游戏,目的不是把从某个洞里出来的地鼠全部打死,而是能够权衡,使总体得分最高,而权衡中的原则是,如果自己与非自己有冲突时,或者正义与利益有冲突时,尽量使非自己开心。
开始工作的前几年,要先建立自己的知识体系,而后,要慢慢建立自己的哲学体系。
审核编辑 :李倩
-
架构师需了解的一些知识2023-05-10 1626
-
阿里专家:架构师是一个什么样的角色2023-03-14 1266
-
什么是 SoC 设计中的系统架构师?2022-07-18 2620
-
云架构师需要具备什么技能2020-03-17 1828
-
女性会更适合做架构师?2019-07-17 2250
-
架构师最重要的是什么2019-07-15 1637
-
关于架构师的详细介绍2019-07-11 1758
-
大数据架构师的职责有哪些2019-04-04 4424
-
怎样成为软件架构师2018-10-19 3459
-
怎样成为一名资深Java架构师2018-10-17 3627
-
NVIDIA火热招聘GPU高性能计算架构师2017-09-01 5012
-
kintex产品架构设计文档(成为架构师也是电子人不错的选...2013-04-30 3243
全部0条评论

快来发表一下你的评论吧 !

