

浅谈AB类音频功率放大器输出中的DC电压漂移
描述
本文介绍一种补偿直接耦合的AB类音频功率放大器输出中的DC电压漂移的技术。
直接耦合输出的主要好处是改善了低音响应。由于该设计省去了隔直电容器,因此其低频传输特性得到了显著改善。
电容器耦合输出
图1显示了一个电容器耦合输出,其中截止低频由负载R(通常为8Ω)和电容器Cc决定。在此示例中,电容器Cc阻止了可能出现在输出中的任何DC偏移。
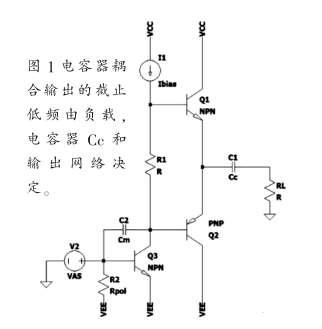
图1电容器耦合输出的截止低频由负载,电容器Cc和输出网络决定。
直接耦合输出
在直接耦合的对象中不是这种情况(图2)。其较低的截止频率不受输出限制,因此前级的任何波动都将导致DC值波动,从而导致直流电流流经负载(扬声器)。除了降低放大器的动态范围和THD之外,这也是为什么有时在打开或关闭分立音频放大器时会听到“喀哒”声的原因。
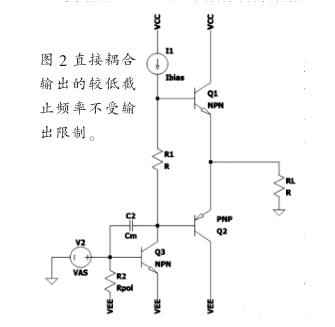
图2直接耦合输出的较低截止频率不受输出限制。
为了纠正此问题,我们将首先进行深入分析,以了解离散双极结型晶体管(BJT)音频放大器的DC偏移背后的原因。接下来,我们将设计一种方法来消除或至少减轻该问题。
首先,创建一个简单的放大器模型,包括主要阶段。
放大器的简单模型图3,这是放大器的简单模型。
顾名思义,VAS(电压放大器级)是一种系统元件,用于放大来自输入的信号,从而通过驱动器级(通常是公共发射器)驱动AB级。驱动器连接到AB级,AB级是互补的射极跟随器,可提供高电流增益。最后,负反馈环路会影响VAS级的增益,从而使整个系统线性且稳定。
VAS级通常使用差分放大器架构构建,其中一侧接收输入信号,另一侧接收负反馈信号。为了简单起见,让我们用一个运算放大器代替VAS(仅用于说明失调问题),并分析级数和失调之间的关系,这在数学上已有所讨论。
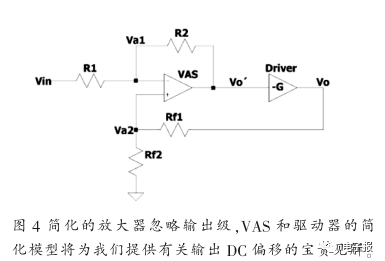
简化的放大器忽略输出级图4 VAS和驱动器的简化模型将为我们提供有关输出DC偏移的宝贵见解。
图4显示了简化的VAS和驱动程序。这个简单的模型将为我们提供有关输出直流偏移的宝贵见解。R1和R2形成局部负反馈,而Rf1和Rf2形成全局负反馈网络。通常为公共发射极级的驱动器产生负增益-G。为简单起见,忽略了AB级,因为对于射极跟随器,电压增益约为-1。
VAS增益由R1和R2之间的关系,R2 》》 R1和Va1 = Va2 = Va确定。驱动器增益非常高,因此整个放大器增益取决于Rf1和Rf2之间的关系:
(Vin-Va)/ R1 =(Va-Vo’)/ R2
Va = Vo ×Rf2 /(Rf2 + Rf1)
替换Va并进行操作,我们得到:
Vin = Vo ×[Rf2 /(Rf2 + Rf1)×(R1 + R2)/ R2 + R1 /(G × R2)]
(R1+ R2)/ R2≅1 R1 /(G × R2)≅0
Vo = Vin ×(Rf2+ Rf1)/ Rf1(1)
这并不是一个令人印象深刻的结论,因此,让我们分析一下Vo与驱动器输入Vo上的电压(接地)之间的关系:
Va1 = Vo’×R1 /(R2 + R1)Va2 = Vo × Rf2 /(Rf2 + Rf1)Va1= Va2
Vo = Vo’×R1 /(R2 + R1)×(Rf2 + Rf1)/ Rf2(2)
最后一个方程式非常重要,因为它显示了驱动器级的直流电压和放大器的输出直流电压之间的关系,表明Vo的较小波动会在Vo中产生较大的偏移。
如前所述,驱动器级通常由一个简单的共发射极级(图1中的Q3)和一个固定所需的基极至发射极电压的小电阻器(Rpol)组成。该晶体管为输出晶体管提供基极电流,因此此阶段的集电极电流在毫安范围内并不罕见。
让我们暂时忘记温度的影响,因此,当我们第一次打开电路时,我们会校准VAS,以使输出DC电压处于VCC和VEE的中间,零伏。如果未施加任何信号,则由于AB级是电压跟随器(共集电极),驱动器晶体管Q3保持大部分VEE电压(VEE-VBE),因此Q3上流过偏置电流IBias,因此Q3消耗了大约功率由下式决定:
PQ3≅VEE× IBias
该功率正在加热Q3,并且该热量以-2.2 mV /°C的已知速率改变了器件的Vbe,从而改变了先前调整的输出DC电压。
如果晶体管开始加热,例如比环境温度高40°C,则其Vbe将下降约88 mV。
在晶体管温度升高时出现的这个较小的Vbe要求使VAS的输出处的Vo‘(电压已在前面解释)相应地发生变化,从而在输出处产生DC电压漂移。
一个真实的例子
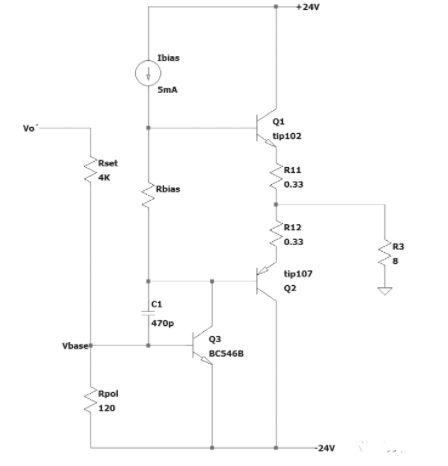
图5中的电路说明了到目前为止已解释的内容。
温度漂移补偿电路图5这是该电路的一阶实际实现。
为了保持较低的失调,将Vo设置为尽可能接近零是很方便的。这就是Rset的目的,Rset代表多圈微调。
这里,基准电压和Vo’之间的关系为:
Vo’=Vbase ×(Rpol + Rset)/ Rpol
因此,基于基极-发射极电压变化的输出电压漂移为:
Vo = Vbase ×(Rpol+ Rset)/ Rpol × R1 /(R2 + R1)×(Rf2 + Rf1)/Rf2(3)
通过这个方程式,我们可以计算出驱动电压的每°C变化,输出电压将变化多少,例如,如果我们给元件分配值(取自真实放大器),例如:
Vo = -2.2mV /°C ×(120 + 4K)/ 120 × 470/(15K + 470)×(2K2 + 10K)/ 2K2
Vo = -12.8 mV/°C
PQ3≅24V× 5mA = 0.12W
假设第三季度采用TO92封装。在这种情况下,可以使用此封装的结至环境热阻来计算结温增量:
Rθja=200°C /瓦
Δ温度=200°C / W × 0.12W = 24°C
ΔVo=24°C ×(-12.8 mV/°C)
ΔVo=-305mV
总之,如果不应用补偿,则输出将漂移约305 mV。这仅考虑了晶体管的自热效应。如果环境温度由于任何原因升高,则此偏移量可能会增加。
如何减轻这种影响
Q3的基极-发射极电压由Rpol固定,因此补偿Vbe电压变化的一种方法是使Rpol以某种方式遵循此变化。这可以通过使用与温度相关的电阻器(如Rpol)连接到晶体管(如热敏电阻)来实现。由于Vbe的变化率为负,因此热敏电阻必须为NTC。
让我们计算Rpol所需的热系数:
IRpol(可以认为是恒定的)流过Rpol,并且Vbe等于VRpol:
Rpol = Vbe / IRpol
(dRpol)/(dVbe)= 1 / IRpol
ΔRpol=1 / IRpol ×ΔVbe
在我们的示例中,Rpol =120Ω和IRpol = 5.6mA,因此:
∆Rpol= 1 / 5.6mA ×(-2.2mV/(°C))
ΔRpol=-0.4Ω/(°C)
我们需要找到在25°C时具有精确热系数和电阻值的热敏电阻。由于这是不可能的,因为大多数NTC热敏电阻具有更高的温度系数,因此解决方案是将一个或多个较高值的热敏电阻与Rpol并联。
这是模拟热敏电阻温度依赖性的方程式:
Rth = Rth0 × eB(1 / T-1 / T0),
其中Rth0是环境温度(我们要计算的)下的热敏电阻电阻,B是参数,通常为3400°K,T为绝对温度,T0为环境温度,约为298.16°K。
因此,环境温度下的斜率可以这样计算:
(dRth)/dT =(-B × Rth0 × eB(1 / T-1 / T0)/ T2)
这是每°C的电阻变化率:
(dRth)/dT = -38.24e – 3 ×Rth0 [Ω/(°C)]
热敏电阻与Rpol并联:
R || =(Rth× Rpol)/(Rth × Rpol),
和:
dR || / dRth = Rpol2/(Rth0 × Rpol)2
这样我们得到了并联电阻的变化:
ΔR||= Rpol2 /(Rth0 ×Rpol)2× ∆Rth
并用每°C的热敏电阻电阻增量代替:
ΔR||= Rpol2 /(Rth0 ×Rpol)2×(-38.24e – 3 × Rth0 [Ω/(°C)])
现在,我们可以为正在分析的示例计算Rth0:
-0.4Ω/(°C)= 1202 /(Rth0 × 120)2 ×(-38.24e – 3 × Rth0 [Ω/(°C)])
Rth0 = 1.12KΩ
为了实用,可以将热敏电阻的值取整至1.2KΩ。
注意事项
热敏电阻应比晶体管小得多,因此热敏电阻的温度将等于或非常接近晶体管外壳的温度。这也将减少热惯性,使系统更快地达到稳态。应使用热粘合剂将热敏电阻连接到晶体管外壳。
测试概念
为了确定该概念对电路的真实行为建模的准确性,我构造了一个测试电路。由于没有1.2KΩ的热敏电阻(NTC 0402),我并联了8个10KΩ的热敏电阻(0402Murata NCP15XH103D03RC)(图6),以产生非常相似的值(1250Ω)。请注意,并联连接热敏电阻不会改变我们计算出的温度系数。
温度传感器图6这是一个1.25KΩ热敏电阻,由八个并联的10KΩ热敏电阻制成。
然后,我使用热粘合剂将传感器连接到Q3的平坦侧,并将其与Rpol(在板的另一侧是SMD电阻器)并联。
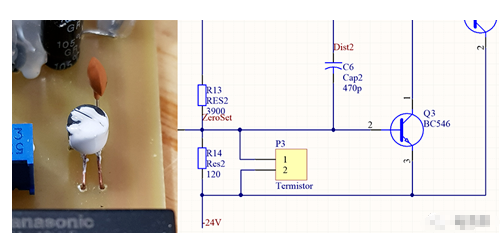
安装的传感器原理图图7先前原理图(图6)中所示的热敏电阻热粘合到Q3。
最后,在这里我们可以看到在连接有(橙色线)和没有(蓝色线)热敏电阻的情况下输出电压漂移,在此状态下,经过大约2分钟后达到了稳态。
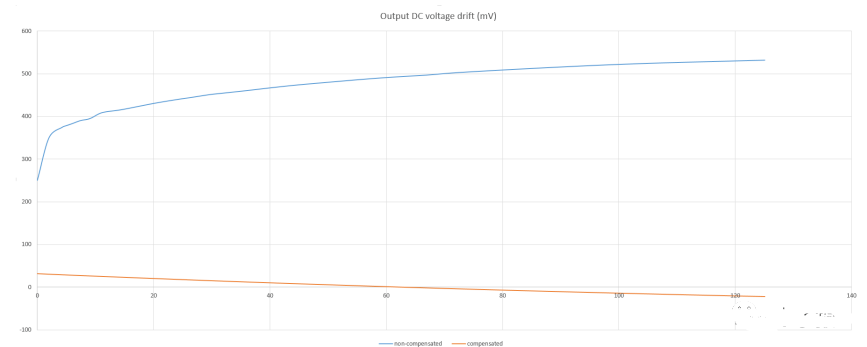
输出电压漂移图图8在这里我们可以看到在连接有(橙色线)和没有(蓝色线)热敏电阻的情况下的输出电压漂移。
阅读更多设计思想电路的补偿响应(橙色线)比未补偿响应(蓝色线)要平坦得多,这表明补偿正在起作用。斜率为负的事实可能意味着它有点补偿过了,但这不是问题,因为直流漂移仍然很小。
还值得一提的是,我们在25°C下计算了所需的温度系数,但热敏电阻不是线性的。这意味着温度系数在整个范围内不是恒定的。但是,由于补偿旨在在有限的温度范围内工作,因此可以忽略热敏电阻的非线性。
-
功率放大器类型有哪些?功率放大器如何选择厂家2017-10-17 0
-
浅谈五极管A1类功率放大器的设计2016-03-10 1279
-
d类音频功率放大器pdf2008-06-23 0
-
功率放大器如何工作的?功率放大器类别和主要指标2023-02-14 0
-
D类音频功率放大器的环路设计2009-12-14 790
-
D类音频功率放大器的研究与设计2016-08-30 1588
-
功率放大器科普:什么是甲乙(AB)型功率放大器2021-12-13 7061
-
AB/D类音频功率放大器NS4110B产品说明2022-02-25 1934
-
AB类音频功率放大器LTK8002D产品手册2022-02-25 2411
-
AB/D类音频功率放大器CS8389产品说明2022-02-25 1062
-
AB/D类音频功率放大器HAA9802产品说明2022-02-25 2277
-
什么是 D类音频功率放大器2022-10-09 6410
-
基于AB类放大器设计的4x50W车用音频功率放大器2023-05-05 1393
-
CLASS-AB类音频功率放大器产品选型指南2024-02-05 2774
-
功率放大器的几种常见类型2024-05-23 3221
全部0条评论

快来发表一下你的评论吧 !

