

一种优化的方法:记忆化搜索
描述
01 故事起源有一天小K去滑雪,雪山高低不平,当然小K只能从高的地方向低的地方滑,那如何选择路线才能滑的最远呢? 把这个问题抽象描述如下:
在一个二维地图中,数值代表此处山的高度,在某个点只能滑向上下左右4个相邻的点,最远的滑行路线,也就等价于找出一条最长的数值下降路线。
比如下图中的红色路线就是此时最长的一条路线,长度为10。那要如何找出这样的一条路线呢?
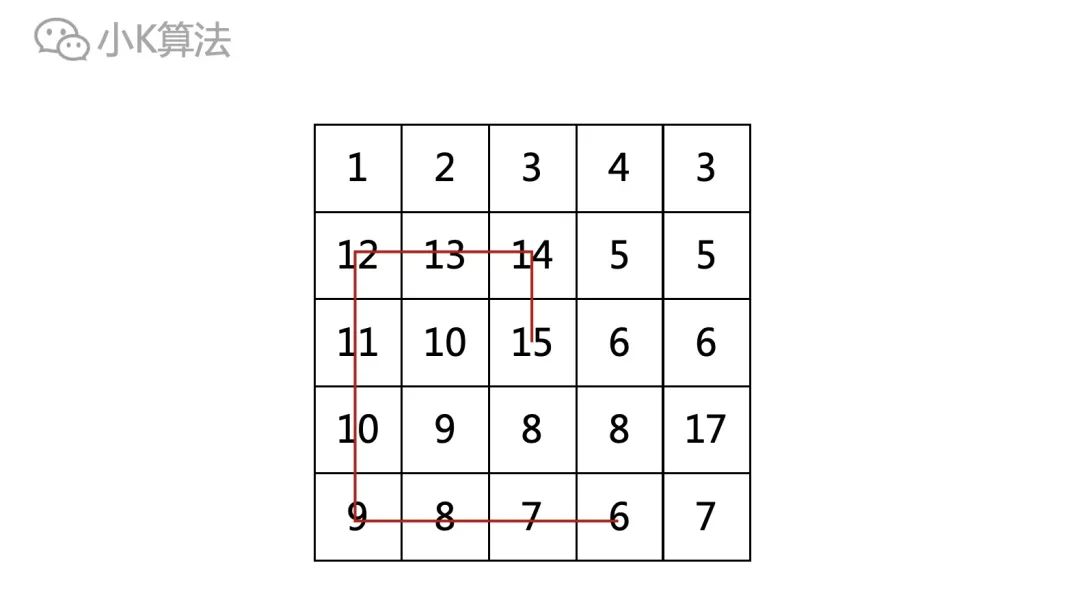 02
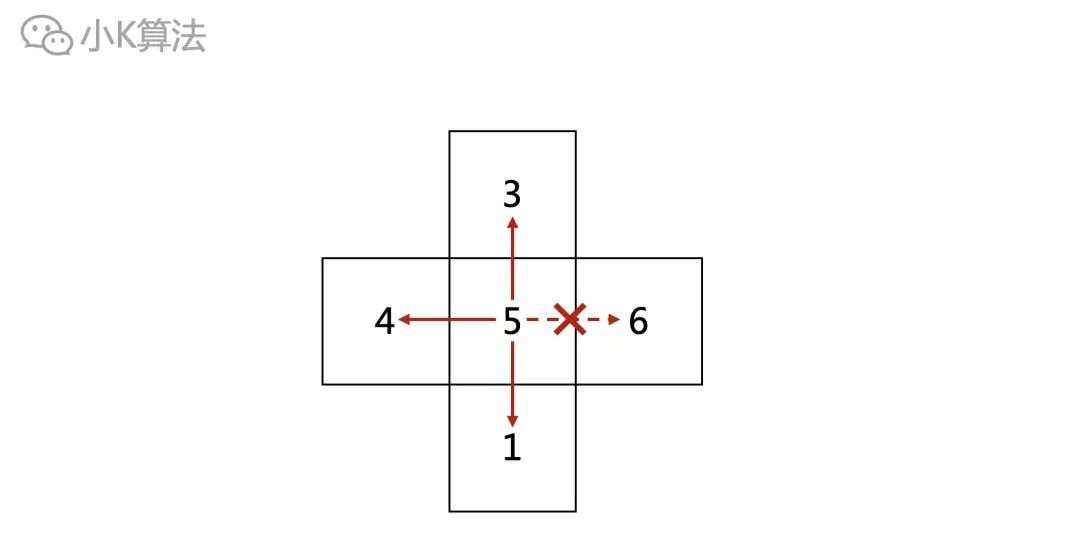
分析在每个点上,只能向周围4个方向滑行,当然前提是此处的高度必须比周围高。
02
分析在每个点上,只能向周围4个方向滑行,当然前提是此处的高度必须比周围高。
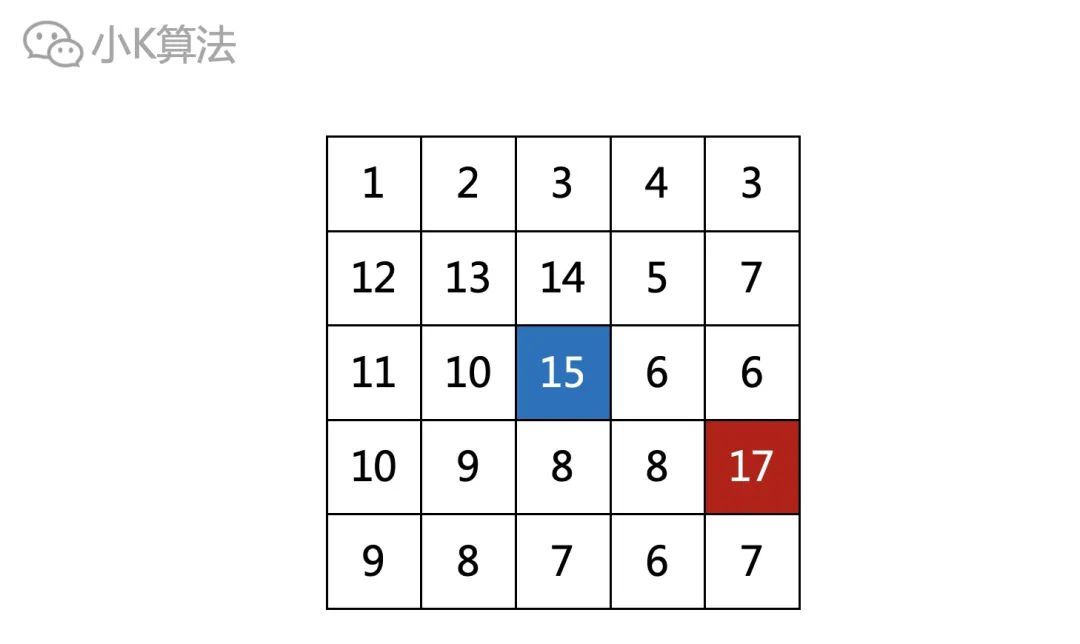
 我们当然可以选择尽可能高的位置出发,比如图中17比15要高。
我们当然可以选择尽可能高的位置出发,比如图中17比15要高。
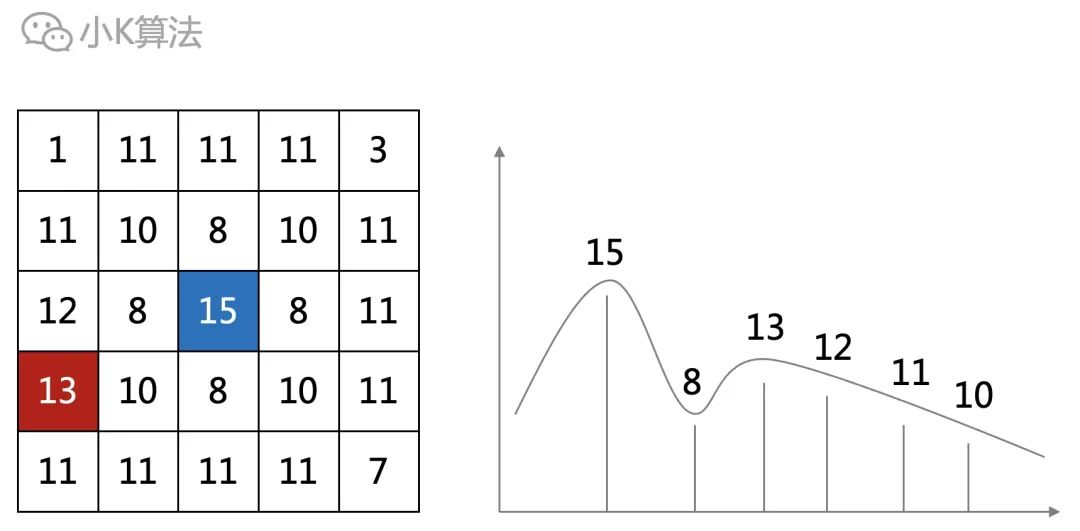
 但这种有可能会陷入局部最优解,比如从下图中的15开始,最大长度为2。而从13开始会更优,长度为5。
但这种有可能会陷入局部最优解,比如从下图中的15开始,最大长度为2。而从13开始会更优,长度为5。
 所以启示我们,不能简单的贪心,而是要考虑全局最优,因为每一个起点都有可能是最优的起点。
所以启示我们,不能简单的贪心,而是要考虑全局最优,因为每一个起点都有可能是最优的起点。那就有了初步的框架了,从每一个起点出发,把可行的路线都找出来,也就是能走的路线都走一遍,再比较全局最优的就行了,而且这也正好符合深搜的算法框架。伪代码
int find(int i,int j){ // 向4个方向尝试 for (i=0->3){ if (ok){ return find(next)+1 } } } int main(){ for (i=0->n) { for (j=0->m) { t=find(i,j) ans=max(ans,t) } } } 03 问题上面的做法可以得到最优解,但有一个问题。如下例,以15为起点的时候,会尝试把6->5->4->3->2->1走一遍。但以16为起点的时候,还会尝试把这条路线走一遍,这就会导致大量的重复计算。
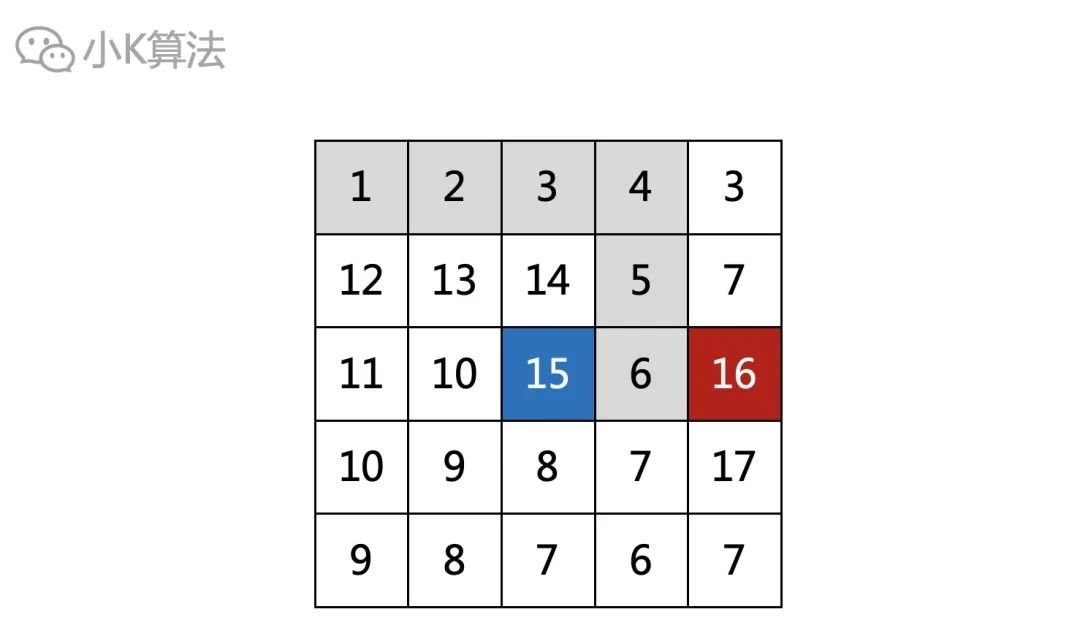 那能不能优化呢? 之所以重复计算,是因为每一次尝试都是重新的开始,它并不知道这条路已经走过了,也就是没有记忆,所以我们引入一种优化的方法,就是记忆化搜索。
04
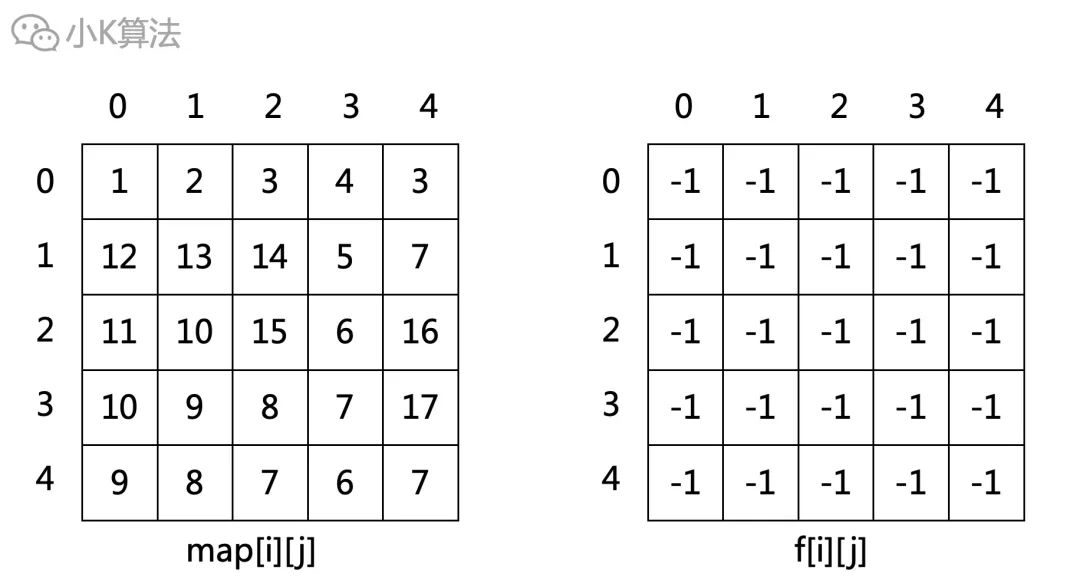
记忆化搜索可以引入一个f[i][j]数组,记录以(i,j)为起点所能找到的最长路线的长度,初始赋值为-1,表示还没有走过。
那能不能优化呢? 之所以重复计算,是因为每一次尝试都是重新的开始,它并不知道这条路已经走过了,也就是没有记忆,所以我们引入一种优化的方法,就是记忆化搜索。
04
记忆化搜索可以引入一个f[i][j]数组,记录以(i,j)为起点所能找到的最长路线的长度,初始赋值为-1,表示还没有走过。
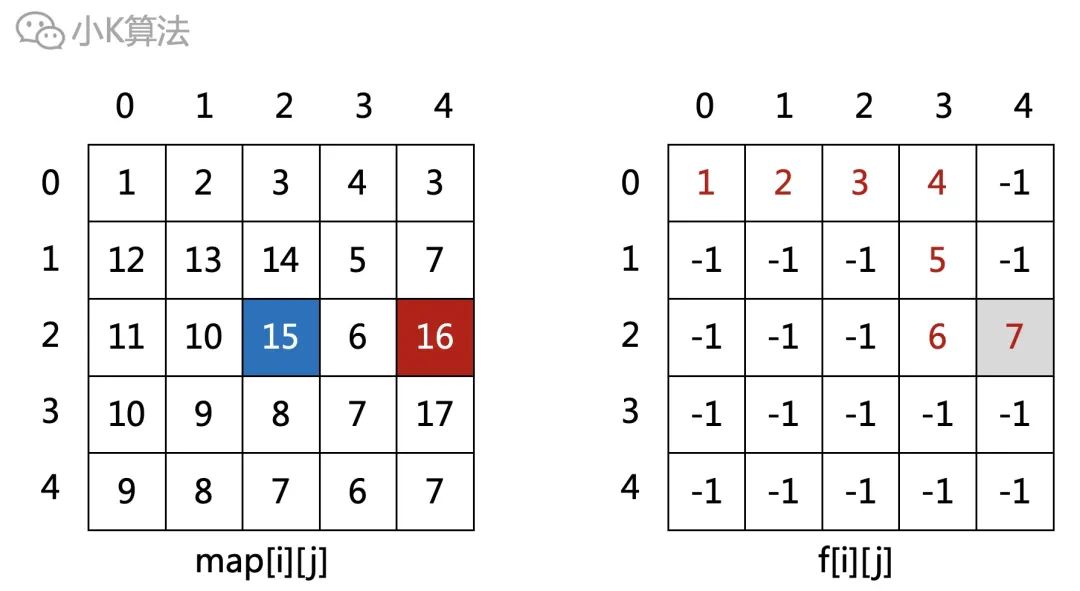
 当走过一点,就将对应的f[i][j]更新为以(i,j)为起点的最大长度。 再回到上面的问题,因为之前肯定走过了(2,3),对应的f[2][3]为6,当尝试从(2,4)出发时,会发现周围已经走过了,只需要更新当前的值+1即可,就避免了重复计算。
当走过一点,就将对应的f[i][j]更新为以(i,j)为起点的最大长度。 再回到上面的问题,因为之前肯定走过了(2,3),对应的f[2][3]为6,当尝试从(2,4)出发时,会发现周围已经走过了,只需要更新当前的值+1即可,就避免了重复计算。
 05
代码实现路线搜索
05
代码实现路线搜索int find(vector<vector<int>> &snowMountain, vector<vector<int>> &f, int i, int j, int r, int c) { int x, y; if (f[i][j] != -1) return f[i][j]; f[i][j] = 1; for (int k = 0; k < 4; k++) { x = i + direction[k][0]; y = j + direction[k][1]; //valid direction if (x >= 0 && x < r && y >= 0 && y < c && snowMountain[i][j] > snowMountain[x][y]) { f[i][j] = maxOfTwo(f[i][j], find(snowMountain, f, x, y, r, c) + 1); } } return f[i][j]; }main函数
int main() { ifstream fin("a.in"); ofstream fout("a.out"); int i, j, r, c, maxHeight = 0; fin >> r >> c; vector<vector<int>> snowMountain(r, vector<int>(c, 0)); vector<vector<int>> f(r, vector<int>(c, -1)); for (i = 0; i < r; i++) for (j = 0; j < c; j++) fin >> snowMountain[i][j]; for (i = 0; i < r; i++) for (j = 0; j < c; j++) { maxHeight = maxOfTwo(maxHeight, find(snowMountain, f, i, j, r, c)); } fout << maxHeight << endl; fin.close(); fout.close(); return 0; } 06 总结记忆化搜索是一种非常实用的算法,因为深搜用递归很容易实现,记忆化又避免了重复子问题的计算,提高了运行效率。 这其实就是动态规划的思想,常见的动态规划用递推实现,相比记忆化搜索实现上会更难一点,而记忆化搜索就没有这个问题。 算法的适用场景也需要根据具体的问题来分析,一般常用在地图或者树型结构中。 审核编辑 :李倩
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
一种线性插值随机对偶平均优化方法2021-05-25 846
-
介绍一种一体化仪表优化交换式测量示例2021-05-11 1866
-
一种基于用户偏好的权重搜索及告警选择方法2021-04-29 780
-
一种改进的深度神经网络结构搜索方法2021-03-16 1054
-
一种利用强化学习来设计mobile CNN模型的自动神经结构搜索方法2018-08-07 4754
-
一种语义规则为指导的增量优化方法2017-12-27 858
-
一种改进的自由搜索算法_任诚2017-03-14 1190
-
PID调节器参数优化设计的一种改进方法2017-01-24 935
-
一种求解动态及不确定性优化问题的新方法2017-01-07 650
-
一种改进的快速搜索算法2010-07-02 1053
-
二重化逆变器谐波抑制的一种优化计算方法2009-12-30 702
-
一种新的记忆多项式预失真器2009-08-08 4321
全部0条评论

快来发表一下你的评论吧 !

