线性反馈移位寄存器(LFSR)

线性反馈移位寄存器(LFSR)：通常由移位寄存器和异或门逻辑组成。其主要应用在：伪随机数，伪噪声序列，计数器，BIST，数据的加密和CRC校验等。

Part.1

线性反馈移位寄存器(LFSR)主要包括两大类：斐波那契(外部LFSR),又称many-to-one；伽罗瓦(内部LFSR),又称one-to-many。

如下图(模2的多项式：x^8+x^6+x^4+1)：

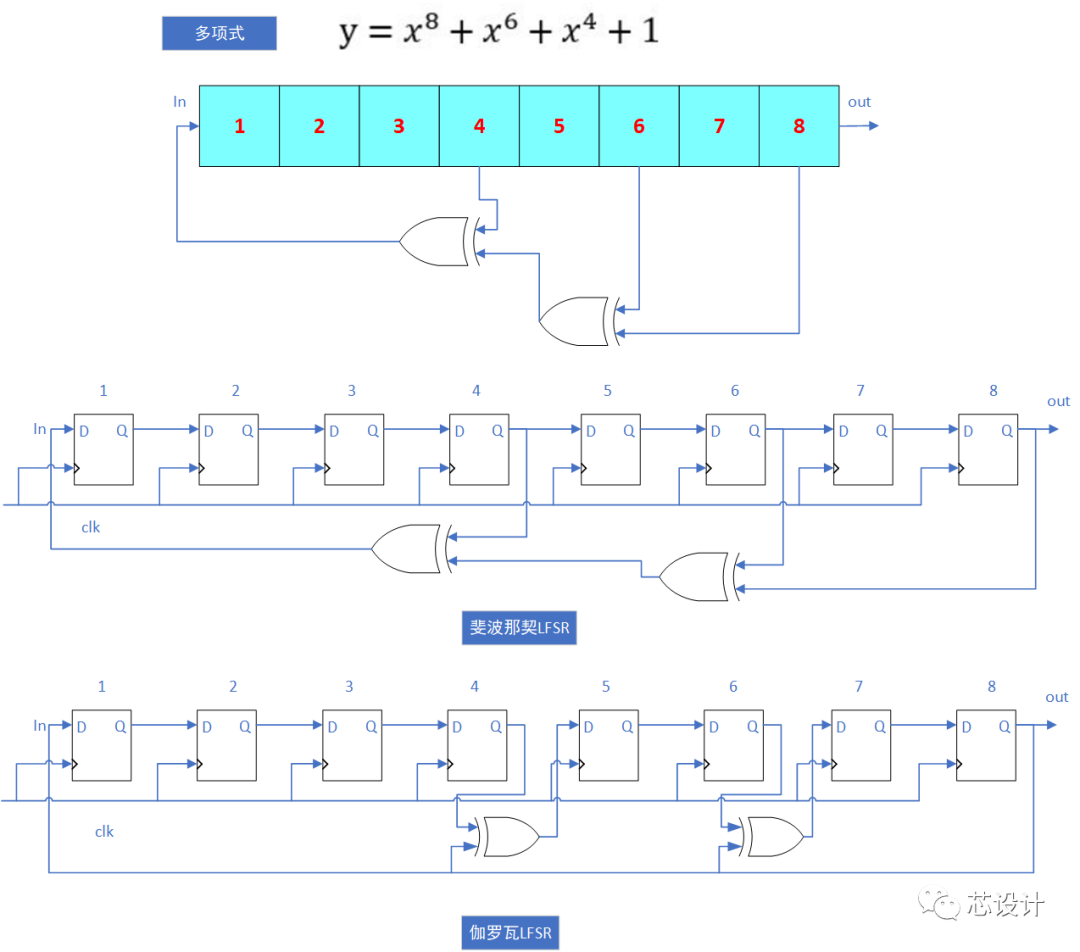
Part.2

抽头(tap)：影响线性反馈寄存器下一个状态的比特位叫做抽头，抽头的设定会决定线性反馈寄存器最大的输出序列长度，抽头通常用有限域算数中模2的多项式来表示（例如模2的多项式为：x^8+x^6+x^4+1）。

      通常N bits的线性反馈寄存器能产生最长的不重复序列为2^N-1。因为当所有寄存器的输出为全零状态时，线性反馈寄存器陷入死循环，故Nbit的线性反馈寄存器的输出状态有2^N-1。

      抽头的位置会影响LSFR的最大输出状态的个数,例如：3bit的抽头为【3,2】会产生7个状态（多项式对应为：x^3+x^2+1)，若抽头为【3,1】会产生2个状态（多项式对应为：x^3+x+1)。

      当N bits下，抽头的设定产生的最大输出序列长度为2^N-1时，此时对应的模2多项式为本原多项式。下表为不同的bits下，抽头的设定（对应不同的本原多项式）和最大的输出状态个数关系表。

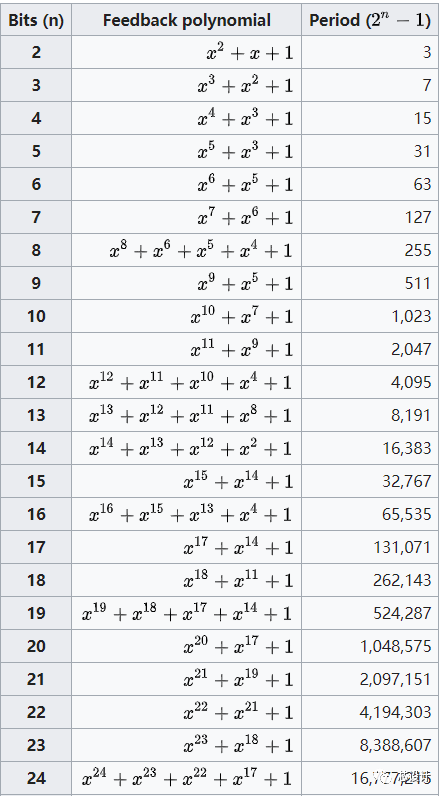
Part.3

上面提到N bits的LFSR能产生最大输出状态的个数为2^N-1，如果输出状态包括全零的状态，最大输出状态的个数可达到2^N，那么通过对LFSR做如下图的修改，即如果检测到Q[7]-Q[0]输出状态为全零时，经过~|Q[6:0]^Q[7]逻辑运算后输出的结果为1，进而保证线性反馈寄存器不会陷入死循环中。

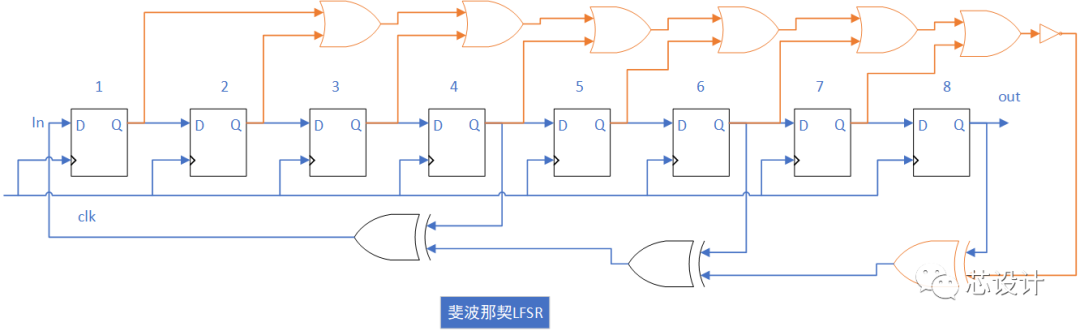
Part.4

在实际的应用中，例如crc的校验，会用到模2的多项式的运算，遵循如下的计算原则：

 

写在最后

这里只是介绍了线性反馈移位寄存器的原理，后面会写到RTL的具体实现。

参考资料： 1.https://en.wikipedia.org/wiki/Linear-feedback_shift_register 2.HDL Chip Design. A Practical Guide for Designing, Synthesizing and Simulating ASICs and FPGAs Using VHDL or Verilog   

审核编辑 ：李倩